Geological hazard susceptibility evaluation based on CF and CF-LR model
-
摘要: 区域地质灾害易发性评价对地质灾害防治具有重要意义。本文以贵州省沿河县为研究区,考虑海拔、坡度、坡向、地形曲率、NDVI、工程地质岩组、断层、道路、水系9个因素,通过相关性分析后作为评价因子。分别利用CF模型和CF-LR模型评价沿河县地质灾害易发性。结果表明:CF模型比CF-LR模型地质灾害易发性等级的频率比值从低易发区到极高易发区明显增大,均有效评价了沿河县地质灾害易发性;CF-LR模型比CF模型AUC值提高了0.096,CF-LR模型具有更高的评价精度。Abstract: The evaluation of regional geological disaster susceptibility is of great significance to the prevention and control of geological disasters. This paper takes Yanhe County in Guizhou Province as the research area, and considers 9 factors including altitude, slope, aspect, terrain curvature, NDVI, engineering geological rock formations, faults, roads, and water systems as evaluation factors. The CF model and the CF-LR model were used to evaluate the susceptibility of geological disasters in Yanhe County. The results show that the frequency ratio between the CF model and the CF-LR model of geological hazard susceptibility levels increases significantly from low-prone areas to extremely high-prone areas, which effectively evaluates the susceptibility of geological hazards in Yanhe County; the CF-LR model compares The AUC value of the CF model is increased by 0.096, and the CF-LR model has a higher evaluation accuracy.
-
0. 引言
地质灾害易发性评价是以地质环境条件为基础,参考地质灾害现状的静态因素来预测一定区域内发生地质灾害的可能性 [1]。地质灾害易发性评价方法分为定性和定量两类。定性方法主要包括专家评分 [2]、层次分析 [3]等。随着数据获取的便利、计算能力的提升以及评估模型的日趋完善,定量评价方法应用更为广泛,定量方法主要有信息量 [4]、确定性系数 [5]、证据权 [6]、逻辑回归 [7]、支持向量机 [8]、决策树 [9]、随机森林 [10]、神经网络 [11]等。其中确定性系数方法计算严密,可以解决多源数据类型的合并问题和影响因子内部不同特征区间对地质灾害易发性的影响 [12],但单一的确定性系数评价法没有考虑每个评价因素对地质灾害易发性的影响差异。逻辑回归( Logistic Regression,LR) 可以使用简单的线性回归来描述自然现象之间的复杂非线性关系,并根据影响因素与历史灾害点之间的关系确定影响因素的权重。文章基于地理信息系统,将研究区划分为栅格,选取海拔、坡度、坡向、地形曲率、归一化植被指数(Normalized Difference Vegetation Index,NDVI)、工程地质岩组、断层、道路、水系这9个孕灾、诱灾因素作为评价指标因子,采用频率比法(Frequency Ratio,FR)、确定性系数法(Certainty Factor,CF)量化评价指标因子,基于确定性系数法进行逻辑回归运算,计算研究区网格地质灾害发生的概率,得到地质灾害易发性分区图。
1. 研究方法
1.1 频率比(FR)
频率比是建立在假设地质条件、孕育地质灾害的概率相似的地区。频率比重点考虑因子类别与地质灾害发生可能性的空间相关性,定量表示环境因子各属性区间对地质灾害发生的相对影响程度 [13-15],计算方法如式(1)。
$$ FR{}_i = \frac{{{{{l_i}} \mathord{\left/ {\vphantom {{{l_i}} L}} \right. } L}}}{{{{s{}_i} \mathord{\left/ {\vphantom {{s{}_i} S}} \right. } S}}} $$ (1) 式中:FRi——频率比值;
li——某个评价因子i类属性区间发生地质灾害的 个数;
L——研究区内的总数;
si——某个评价因子i类区间的面积;
S——研究区总面积。
FRi大于 1 表明该环境因子属性区间利于地质灾害发育,值越大表示对地质灾害发育的贡献也越大;反之,FRi小于 1 表明该环境因子属性区间不利于地质灾害发育。
1.2 确定性系数模型(CF)
确定性系数模型假设将来发生地质灾害的条件和过去发生地质灾害的条件相同。CF 计算公式为:
$$ CF = \left\{ \begin{aligned} &\frac{{P{P_{\rm{a}}} - P{P_{\rm{S}}}}}{{P{P_S}(1 - P{P_{\rm{a}}})}} \quad (P{P_{\rm{a}}} < P{P_{\rm{S}}})\\ &\frac{P{P_{\rm{a}}} - P{P_{\rm{S}}}}{{P{P_{\rm{a}}}(1 - P{P_{\rm{S}}})}} \quad (P{P_{\rm{a}}} \geqslant P{P_{\rm{S}}}) \end{aligned} \right.$$ (2) 式中:CF——地质灾害发生的确定性系数;
PPa——地质灾害在因子分类数据a中发生的条件 概率,研究中通常用因子分类a中的地质 灾害个数与因子分类a的面积比值表示;
PPS——地质灾害在整个研究区中发生的先验概率, 以研究区地质灾害总个数与研究区总面 积比值表示。
由式(2)可知,CF的变化区间为[−1,1]。正值表示地质灾害发生的确定性大,越接近1越易于发生地质灾害;负值表示地质灾害发生确定性小,越接近−1越不易于发生地质灾害;值为 0 时表示条件概率和先验概率相同,不确定是否会发生地质灾害 [5]。
1.3 基于确定性系数的逻辑回归模型(CF-LR)
逻辑回归模型是研究二分类因变量常用的多元统计分析方法。自变量Xi 为控制灾害发生的影响因子。因变量Y属于二分类变量,通常 0 代表地质灾害不存在,1 代表地质灾害存在。用线性回归来描述自然现象之间复杂的非线性关系,揭示因变量和多个自变量之间的多元回归关系,将每个评价因子视为自变量,能很好解决滑坡易发性评价中出现的二分类变量问题 [16],逻辑回归函数如式(3):
$$ \left.\begin{aligned} Z={\beta }_{0}+{\beta }_{1}{x}_{1}+{\beta }_{2}{x}_{2}+\cdots +{\beta }_{n}{x}_{n}\\ P({Y}=1)=\frac{1}{1+{{\rm{e}}}^{-Z}}\end{aligned}\right\} $$ (3) 式中:P——地质灾害发生的概率;
Z——地质灾害发生概率的目标函数,表达为各因素自变量x1,x2,x3
$,\cdots, $ xn的线性组合;${\beta }_{1},{\beta }_{2},\cdots, {\beta }_{{n}}$ ——逻辑回归系数;β0——常数表示在不受任何有利或不利于地质灾害发生因素影响的条件下,地质灾害发生与不发生概率之比的对数值 [17]。
通过确定性系数模型计算得到各评价因子类别的值,将其结果作为逻辑回归模型中的自变量,建立回归方程,进行逻辑回归运算,得到各评价因子的逻辑回归系数,以此进行确定性系数–逻辑回归模型(CF-LR)进行地质灾害易发性评价。
2. 实例分析
2.1 研究区概况
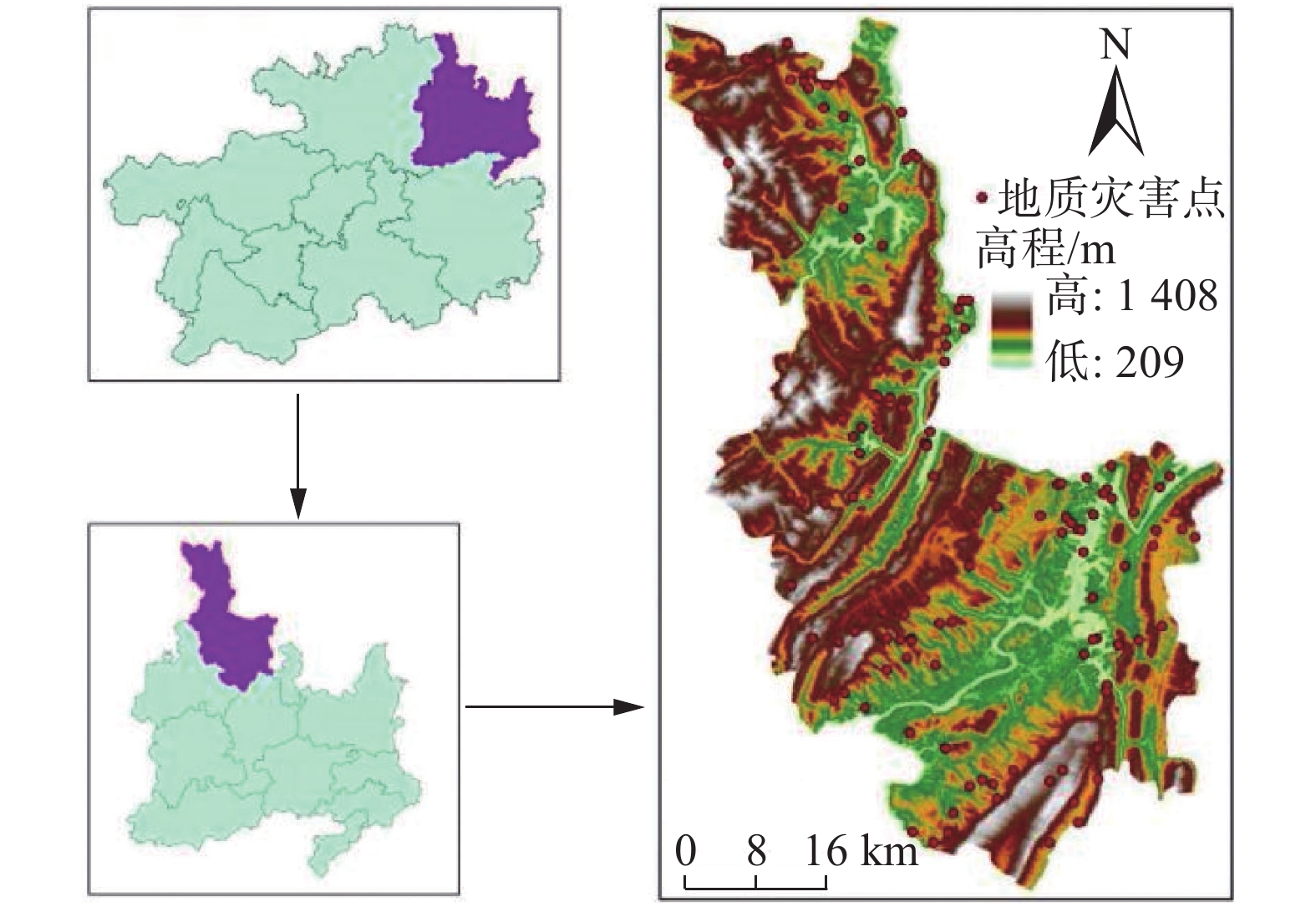
研究区沿河土家族自治县位于贵州省东北部,隶属铜仁市,南北长98.28 km,东西宽53 km,行政区域总面积2483.51km2,占贵州省总面积的1.4%,占铜仁市总面积的13.7%。沿河县境内有乌江及其支流洪渡河、暗溪河、白泥河、坝坨河等26条河流,河道长548.7 km,河网密度0.23 km/km2。地貌轮廓明显受地质构造控制,全县地貌“轴部成山,翼部成谷”。区内出露地层从老到新有震旦系、寒武系、奥陶系、志留系、二叠系、三叠系及第四系。受乌江切割和地层、岩性、构造的影响,在内外营力综合作用下,形成山峦叠障、沟谷纵横、复杂多样的地形地貌景观。区内历史地质灾害以滑坡、崩塌为主,共计130处,滑坡、崩塌分别占全县地质灾害的55.38%、33.85%。研究区地理位置及地质灾害分布如图1所示。
2.2 评价指标因子选取
结合研究区的地质背景、地质灾害形成条件及发育特征,初步选取海拔、坡度、坡向、地形曲率、归一化植被指数(NDVI)、工程地质岩组、距断层距离、距道路距离、距水系距离9个影响因素作为评价指标因子。数据源为沿河县地质灾害数据库、地理空间数据云平台获取研究区30 m×30 m数字高程模型(Digital Elevation Model,DEM)、1∶50 000的地质图、Google影像地图,利用ArcGIS平台通过DEM数据提取分析得到研究区坡度、坡向、地形曲率、河流网评价因子图层,通过Google影像地图矢量化得到道路数据,利用 landsat8 影像获得该区的归一化植被指数(NDVI)专题图。
2.3 评价因子相关性分析
影响地质灾害发育的因素之间存在一定的关联,当评价因子之间存在多重共线问题时,会降低模型的预测精度,因而需对评价因素进行相关性分析。利用ArcGIS计算相关矩阵如表1所示,相关性系数绝对值最大为0.324,说明本文选取的9个评价指标因子之间相关性较弱,均可纳入研究区评价模型 [18]。
表 1 评价指标因子相关性系数矩阵Table 1. Correlation coefficient matrix of evaluation index factors评价因子 海拔 坡度 坡向 地形曲率 NDVI 工程地质岩组 断层缓冲区 道路缓冲区 河流缓冲区 海拔 1 坡度 −0.009 1 坡向 0.009 0.059 1 地形曲率 0.138 0.045 −0.004 1 NDVI 0.154 0.094 −0.073 0.032 1 工程地质岩组 −0.004 0.004 −0.016 −0.010 −0.006 1 断层缓冲区 0.182 −0.002 0.002 0.004 0.024 0.104 1 道路缓冲区 0.113 0.081 0.004 0.009 0.043 0.007 0.060 1 河流缓冲区 0.324 −0.042 0.006 0.024 0.059 0.075 0.094 0.146 1 2.4 评价指标因子分析
工程地质岩组为离散型因子,根据野外地质调查以及已有分类标准进行分类,连续型指标因子分类根据地质灾害比例进行等距离划分,各指标因子分级如图2所示,利用式(1)进行频率比计算确定性系数计算,利用式(2)进行确定性系数计算,结果见表2。
表 2 评价指标因子分级、频率比、确定性系数Table 2. Evaluation index factor classification, frequency ratio and certainty coefficient评价指
标因子分级 地质灾
害频数分级面积
/km2频率比 CF 评价指
标因子分级 地质灾
害频数分级面积
/km2频率比 CF 工程地
质岩组坚硬岩组 19 908.650 0.399 −0.374 地形
曲率<−0.2 54 842.320 1.225 0.194 较坚硬岩组 12 433.841 0.528 −0.485 −0.2~0.2 41 804.509 0.974 −0.028 较软岩组 24 354.624 1.293 0.239 ≥0.2 35 836.681 0.799 −0.210 软岩组 24 156.908 2.922 0.694 道路缓
冲区/m0~200 10 121.608 1.571 0.384 软硬相间岩组 51 629.487 1.548 0.373 200~400 7 110.030 1.215 0.187 海拔/m 209~400 19 125.528 2.892 0.690 400~600 8 102.096 1.497 0.350 400~600 35 630.016 1.061 0.061 600~800 8 96.148 1.590 0.391 600~800 46 781.436 1.125 0.117 800~1000 4 91.358 0.836 −0.206 800~1000 23 557.591 0.788 −0.221 ≥1000 93 1962.270 0.905 −0.099 1000~1200 5 329.869 0.290 −0.721 河流缓
冲区/m0~200 18 292.050 1.177 0.159 1200~1408 2 59.068 0.647 −0.366 200~400 20 270.762 1.411 0.307 坡度/(°) 0~8 8 360.777 0.424 −0.589 400~600 16 276.547 1.105 0.112 8~16 44 774.534 1.085 0.083 600~800 15 263.664 1.087 0.084 16~24 47 726.415 1.236 0.202 800~1000 13 249.447 0.996 −0.005 24~32 24 407.503 1.125 0.117 ≥1000 48 1131.039 0.811 −0.198 32~40 5 150.886 0.633 −0.380 断层缓
冲区/m0~300 15 263.922 1.086 0.083 ≥40 2 63.395 0.603 −0.410 300~600 13 246.968 1.006 0.006 坡向 平面 0 9.052 0.000 −1.000 600~900 13 230.345 1.078 0.077 北 17 249.994 1.299 0.243 900~1200 10 202.012 0.946 −0.057 东北 19 325.920 1.114 0.108 1200~1500 8 176.901 0.864 −0.143 东 32 390.819 1.564 0.381 ≥1500 71 1363.363 0.995 −0.005 东南 14 338.893 0.789 −0.220 NDVI −0.02~0.1 9 219.331 0.784 −0.225 南 9 253.127 0.679 −0.333 0.1~0.2 25 459.478 1.039 0.040 西南 21 287.807 1.394 0.298 0.2~0.3 61 1008.861 1.155 0.142 西 7 326.164 0.410 −0.603 0.3~0.4 34 757.656 0.857 −0.149 西北 11 301.734 0.696 −0.315 0.4~0.54 1 38.183 0.500 −0.513 海拔高度与降雨量、植被类型、植被覆盖等有着密切的关系,影响着人类工程活动程度,因此海拔间接影响着地质灾害的发育 [19],海拔高度209~1408 m,将其分为6个类别。
坡度定量描述地面的倾斜程度,它的大小对斜坡表面径流量、斜坡表体土层剩余下滑力等都影响巨大,一定程度上影响着地质灾害发育的规模与强度 [20],研究区坡度最高达75°,以8°等间距分为5类,大于40°为1类,共计6个类别。
不同坡向与岩体结构面的组合关系差异导致地质灾害发育的程度不同 [21],将研究区坡向分为9个类别。
地形曲率是局部地形曲面在各个截面方向上形状、凹凸变化的反映,其值为正时表明边坡是凸面坡,为 0 时表明为平面坡,为负时表明边坡为凹面坡 [22],由于研究区平面坡(曲率等于0)面积极小,所以用曲率为−0.2~0.2代表近似平面坡,将其分为凹坡(<−0.2),近似平面坡(−0.2~0.2),凸坡(≥0.2)3类。
归一化植被指数(NDVI)是遥感影像中近红外波段(NIR)的反射值和红光波段(R)的反射值的差与两者之和的比值,NDVI值的范围为 [−1 , 1],负值表示对可见光高反射,地面为江、河、湖泊等水体或有雪覆盖,0表示NIR和R近似相等,为岩石或裸地等,正值表示有植被覆盖,数值越大表示植被覆盖率越高 [23],研究区NDVI在−0.02~0.54之间,将其分为5个类别。
岩土体是地质灾害发生的物质来源基础,岩石类型、坚硬程度决定岩土体的力学强度、抗风化能力和抗侵蚀能力 [19],研究区工程地质岩组分为5类,分别为坚硬岩组、较坚硬岩组、较软岩组、软岩组和软硬相间岩组。
地质构造影响着岩体结构及其组合特征,对山区地质灾害发育起着重要的控制作用 [24],利用ArcGIS领域分析功能将研究区断层以300 m等距离提取缓冲区,得到6个类别。
道路修建开挖坡体改变原有地质环境,破坏岩土体结构 [25],以200 m等距离提取道路缓冲区,得到6个类别。
河流的侵蚀、侧蚀作用影响地质灾害的发育、且河流是控制坡面侵蚀的重要原因 [26],将研究区河流200 m等距离提取缓冲区,得到6个类别。
通过对因子类别进行分类后,利用式(1)对各评价因子类别进行频率比计算,当频率比大于1时,说明该因子类别对地质灾害发育具有促进作用,如表3所示。
表 3 频率比大于1的属性区间Table 3. Attribute intervals with frequency ratio greater than 1评价因子 海拔/m 坡度/(°) 坡向 地形曲率 NDVI 工程地质岩组 断层缓冲区/m 道路缓冲区/m 河流缓冲区/m 频率比大于
1类别209~400 8~16 北 < −0.2 0.1~0.2 较软质岩 0~300 0~200 0~200 400~600 16~24 东北 0.2~0.3 软质岩 300~600 200~400 200~400 600~800 24~32 东 软硬相间质岩 600~900 400~600 400~600 西南 600~800 600~800 2.5 逻辑回归分析
利用ArcGIS以500 m距离制作灾点缓冲区,在500 m以外提取随机点130个非地质灾害点,与灾害训练样本组成训练集共计260个点。将9个评价指标因子的属性提取至训练集样本,导出后替换成评价因子的CF值导入SPSS软件中进行逻辑回归运算,各评价因子分类级别的CF值作为自变量,是否发生滑坡灾害作为因变量(0 表示未发生地质灾害,1值表示已发生地质灾害),LR-CF模型的逻辑回归运算结果如表4所示,其计算得到的所有评价指标因子的逻辑回归系数均为正数,表明所有评价指标因子对模型均起正向作用。在逻辑回归计算过程中,显著性sig ≤ 0. 05 则该回归系数有效,评价指标因子具有统计意义 [22]。
表 4 逻辑回归系数和显著性Table 4. Logistic regression coefficient and significance评价因子 海拔 坡度 坡向 地形曲率 NDVI 工程地质岩组 断层缓冲区 道路缓冲区 河流缓冲区 常量 β 3.844 2.495 3.418 4.085 1.198 4.377 3.218 0.734 2.728 2.604 sig 0.000 0.003 0.000 0.019 0.023 0.000 0.027 0.036 0.130 0.000 3. 易发性分区与评价
3.1 CF、CF-LR分区结果
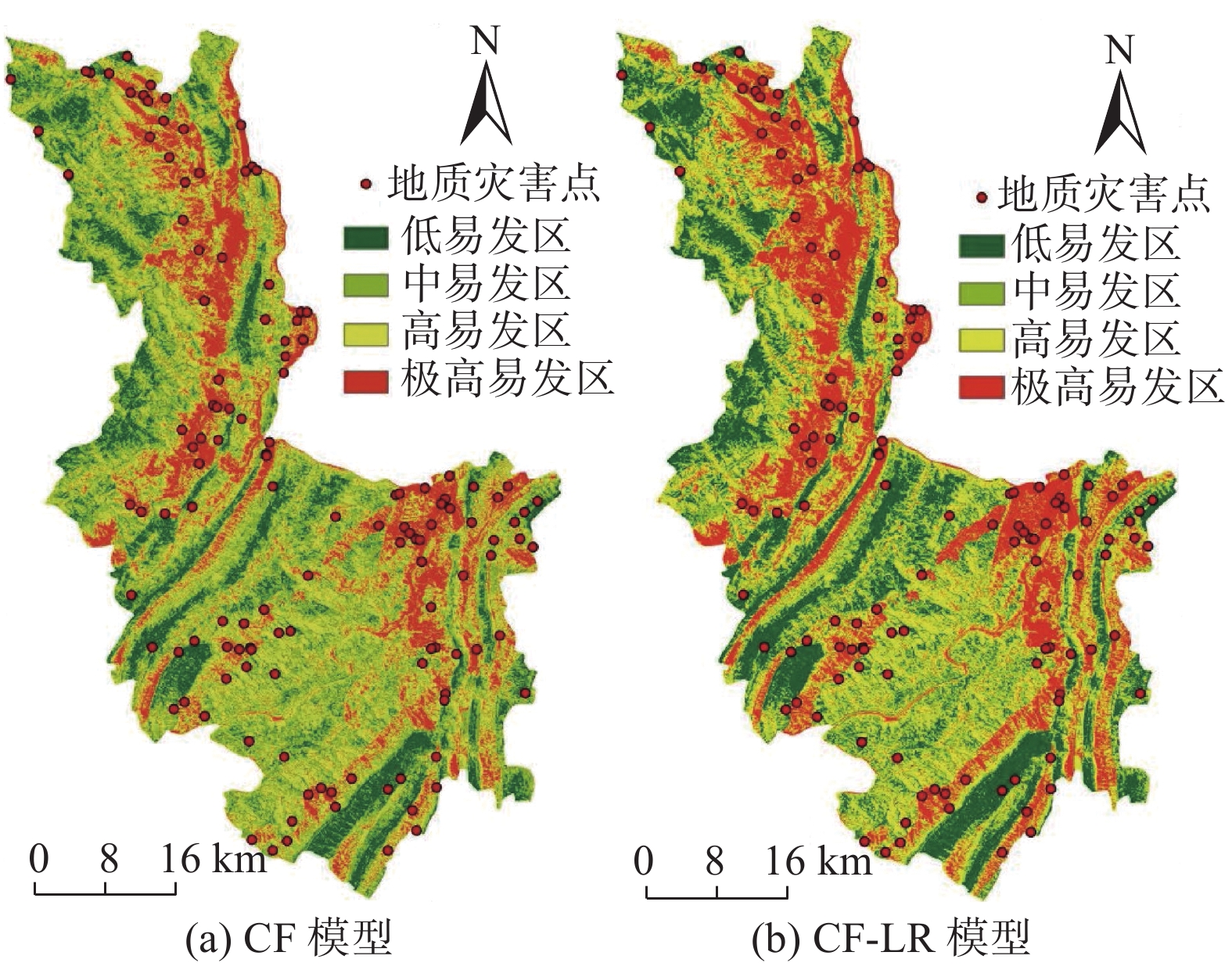
基于GIS平台,将评价指标因子图层自定义添加属性字段,对应输入计算的确定性系数,利用栅格叠加得到确定性系数模型评价图,利用自然断点法将沿河县地质灾害易发性区划为低易发区、中易发区、高易发区、极高易发区,其面积(频率比)分别为361.265 km2(0.159)、784.269 km2(0.414)、895.197 km2(1.003)、442.779 km2(2.718),如图3(a)和表5所示。利用栅格计算器按照公式(3)计算得到CF-LR模型地质灾害发生概率图,利用自然断点法将其分为低易发区、中易发区、高易发区、极高易发区,其面积(频率比)分别为671.252 km2(0.142)、467.758 km2(0.327)、927.527 km2(0.741)、507.145 km2(3.051),如图3(b)和表5所示。CF模型和CF-LR模型地质灾害易发性等级的频率比值均从极低易发区到极高易发区明显增大,表明有效评价了研究区地质灾害易发性。CF模型和CF-LR模型计算的极高易发区频率比值分别占总频率比值为63.3%和71.6%。说明CF-LR模型比单一CF模型评价精度更高。
表 5 地质灾害易发性评价频率比值Table 5. Frequency ratio of geological hazard susceptibility evaluation评价模型 易发性
等级分级面积
/km2面积
占比灾害点
频数灾害
占比频率比 CF 低易发区 361.265 0.145 3 0.023 0.159 中易发区 784.269 0.316 17 0.131 0.414 高易发区 895.197 0.360 47 0.362 1.003 极高易发区 442.779 0.178 63 0.485 2.718 CF-LR 低易发区 671.252 0.270 5 0.038 0.142 中易发区 467.758 0.188 8 0.062 0.327 高易发区 927.527 0.373 36 0.277 0.741 极高易发区 507.145 0.204 81 0.623 3.051 3.2 精度验证
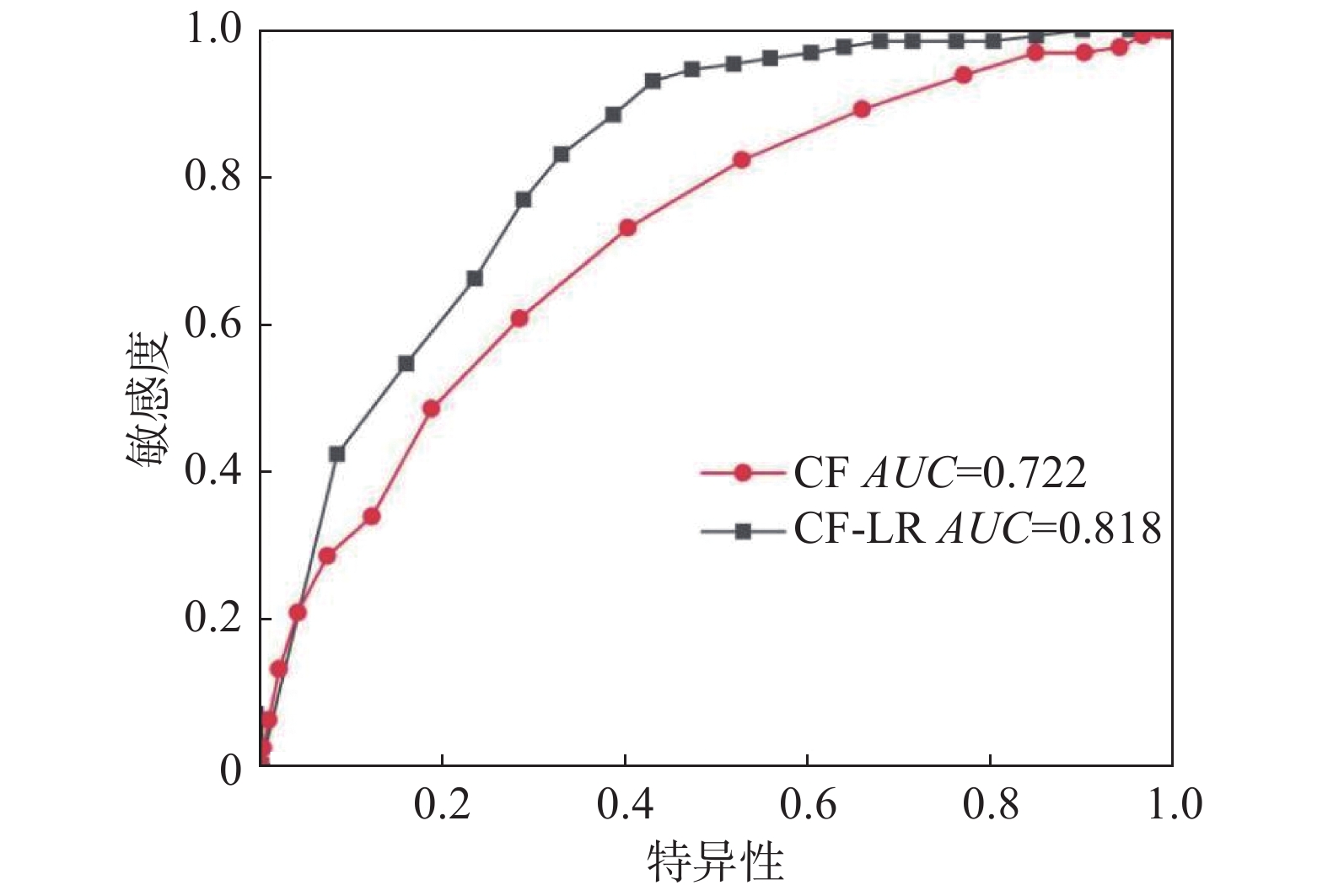
本文使用ROC曲线来表示拟合数据和实测数据之间的关系,评价成功率或有效性以AUC值来表示(图4)。曲线中纵轴为敏感度,即实际地质灾害数量百分比累加量,横轴为特异性,即易发性面积百分比累积量,ROC曲线下面积AUC值越大表明模型评估效果越好 [27-28]。CF模型和CF-LR模型AUC值分别为0.722和0.818,说明CF和CF-LR评价模型均能够较为客观准确地对沿河县地质灾害易发性进行评价,且CF法进行逻辑回归后的CF-LR模型评价精度更高。
4. 结论
(1)文中从选取的9个地质灾害影响因素的各类别的频率比值可以看出,在海拔209~800 m,坡度8°~32°,坡向朝向北、东北、东、西南,地形曲率小于−0.2,NDVI为0.1~0.3,较软质岩、软质岩、软硬相间质岩,距断层900 m、道路和河流800 m以内对沿河县地质灾害发育具有促进作用。
(2)CF模型评价低易发区、中易发区、高易发区、极高易发区,其面积(频率比)分别为361.265 km2(0.159)、784.269 km2(0.414)、895.197 km2(1.003)、442.779 km2(2.718);CF-LR模型评价低易发区、中易发区、高易发区、极高易发区,其面积(频率比)分别为671.252 km2(0.142)、467.758 km2(0.327)、927.527 km2(0.741)、507.145 km2(3.051)。CF模型和CF-LR模型地质灾害易发性等级的频率比值从极低易发区到极高易发区明显增大,均有效评价了研究区地质灾害易发性。CF模型和CF-LR模型计算的极高易发区频率比值分别占总频率比值为63.3%和71.6%。
(3)CF模型和CF-LR模型AUC值分别为0.722和0.818,均能够较为客观准确地对沿河县地质灾害易发性进行评价。但单一CF法没有考虑评价因素对地质灾害易发性的影响差异,在此基础上,LR法用线性回归来表示评价因子之间复杂非线性关系,考虑了评价因子的权重,使得AUC值提高了0.096,CF-LR模型具有更高的评价精度。
由于研究区的地质灾害研究样本偏少,不为理想研究实验区,将影响评价效果和精度,对地质灾害易发性评价的精度还需进一步探索。
-
表 1 评价指标因子相关性系数矩阵
Table 1 Correlation coefficient matrix of evaluation index factors
评价因子 海拔 坡度 坡向 地形曲率 NDVI 工程地质岩组 断层缓冲区 道路缓冲区 河流缓冲区 海拔 1 坡度 −0.009 1 坡向 0.009 0.059 1 地形曲率 0.138 0.045 −0.004 1 NDVI 0.154 0.094 −0.073 0.032 1 工程地质岩组 −0.004 0.004 −0.016 −0.010 −0.006 1 断层缓冲区 0.182 −0.002 0.002 0.004 0.024 0.104 1 道路缓冲区 0.113 0.081 0.004 0.009 0.043 0.007 0.060 1 河流缓冲区 0.324 −0.042 0.006 0.024 0.059 0.075 0.094 0.146 1 表 2 评价指标因子分级、频率比、确定性系数
Table 2 Evaluation index factor classification, frequency ratio and certainty coefficient
评价指
标因子分级 地质灾
害频数分级面积
/km2频率比 CF 评价指
标因子分级 地质灾
害频数分级面积
/km2频率比 CF 工程地
质岩组坚硬岩组 19 908.650 0.399 −0.374 地形
曲率<−0.2 54 842.320 1.225 0.194 较坚硬岩组 12 433.841 0.528 −0.485 −0.2~0.2 41 804.509 0.974 −0.028 较软岩组 24 354.624 1.293 0.239 ≥0.2 35 836.681 0.799 −0.210 软岩组 24 156.908 2.922 0.694 道路缓
冲区/m0~200 10 121.608 1.571 0.384 软硬相间岩组 51 629.487 1.548 0.373 200~400 7 110.030 1.215 0.187 海拔/m 209~400 19 125.528 2.892 0.690 400~600 8 102.096 1.497 0.350 400~600 35 630.016 1.061 0.061 600~800 8 96.148 1.590 0.391 600~800 46 781.436 1.125 0.117 800~1000 4 91.358 0.836 −0.206 800~1000 23 557.591 0.788 −0.221 ≥1000 93 1962.270 0.905 −0.099 1000~1200 5 329.869 0.290 −0.721 河流缓
冲区/m0~200 18 292.050 1.177 0.159 1200~1408 2 59.068 0.647 −0.366 200~400 20 270.762 1.411 0.307 坡度/(°) 0~8 8 360.777 0.424 −0.589 400~600 16 276.547 1.105 0.112 8~16 44 774.534 1.085 0.083 600~800 15 263.664 1.087 0.084 16~24 47 726.415 1.236 0.202 800~1000 13 249.447 0.996 −0.005 24~32 24 407.503 1.125 0.117 ≥1000 48 1131.039 0.811 −0.198 32~40 5 150.886 0.633 −0.380 断层缓
冲区/m0~300 15 263.922 1.086 0.083 ≥40 2 63.395 0.603 −0.410 300~600 13 246.968 1.006 0.006 坡向 平面 0 9.052 0.000 −1.000 600~900 13 230.345 1.078 0.077 北 17 249.994 1.299 0.243 900~1200 10 202.012 0.946 −0.057 东北 19 325.920 1.114 0.108 1200~1500 8 176.901 0.864 −0.143 东 32 390.819 1.564 0.381 ≥1500 71 1363.363 0.995 −0.005 东南 14 338.893 0.789 −0.220 NDVI −0.02~0.1 9 219.331 0.784 −0.225 南 9 253.127 0.679 −0.333 0.1~0.2 25 459.478 1.039 0.040 西南 21 287.807 1.394 0.298 0.2~0.3 61 1008.861 1.155 0.142 西 7 326.164 0.410 −0.603 0.3~0.4 34 757.656 0.857 −0.149 西北 11 301.734 0.696 −0.315 0.4~0.54 1 38.183 0.500 −0.513 表 3 频率比大于1的属性区间
Table 3 Attribute intervals with frequency ratio greater than 1
评价因子 海拔/m 坡度/(°) 坡向 地形曲率 NDVI 工程地质岩组 断层缓冲区/m 道路缓冲区/m 河流缓冲区/m 频率比大于
1类别209~400 8~16 北 < −0.2 0.1~0.2 较软质岩 0~300 0~200 0~200 400~600 16~24 东北 0.2~0.3 软质岩 300~600 200~400 200~400 600~800 24~32 东 软硬相间质岩 600~900 400~600 400~600 西南 600~800 600~800 表 4 逻辑回归系数和显著性
Table 4 Logistic regression coefficient and significance
评价因子 海拔 坡度 坡向 地形曲率 NDVI 工程地质岩组 断层缓冲区 道路缓冲区 河流缓冲区 常量 β 3.844 2.495 3.418 4.085 1.198 4.377 3.218 0.734 2.728 2.604 sig 0.000 0.003 0.000 0.019 0.023 0.000 0.027 0.036 0.130 0.000 表 5 地质灾害易发性评价频率比值
Table 5 Frequency ratio of geological hazard susceptibility evaluation
评价模型 易发性
等级分级面积
/km2面积
占比灾害点
频数灾害
占比频率比 CF 低易发区 361.265 0.145 3 0.023 0.159 中易发区 784.269 0.316 17 0.131 0.414 高易发区 895.197 0.360 47 0.362 1.003 极高易发区 442.779 0.178 63 0.485 2.718 CF-LR 低易发区 671.252 0.270 5 0.038 0.142 中易发区 467.758 0.188 8 0.062 0.327 高易发区 927.527 0.373 36 0.277 0.741 极高易发区 507.145 0.204 81 0.623 3.051 -
[1] 倪化勇, 王德伟, 陈绪钰, 等. 四川雅江县城地质灾害发育特征与稳定性评价[J]. 现代地质,2015,29(2):474 − 480. [NI Huayong, WANG Dewei, CHEN Xuyu, et al. Formation characteristics and stability assessment of geological hazards in Yajiang City, Sichuan Province[J]. Geoscience,2015,29(2):474 − 480. (in Chinese with English abstract) DOI: 10.3969/j.issn.1000-8527.2015.02.036 [2] 牛全福. 基于GIS的地质灾害风险评估方法研究: 以“4·14”玉树地震为例[D]. 兰州: 兰州大学, 2011 NIU Quanfu. Study on the method of geological disaster risk assessment based on GIS: A case study in “4.14” Yushu earthquake[D]. Lanzhou: Lanzhou University, 2011. (in Chinese with English abstract)
[3] 王哲, 易发成. 基于层次分析法的绵阳市地质灾害易发性评价[J]. 水文地质工程地质,2007,34(3):93 − 98. [WANG Zhe, YI Facheng. Evaluation of geological hazard probability of occurrence based on analytical hierarchy process in Mianyang City[J]. Hydrogeology & Engineering Geology,2007,34(3):93 − 98. (in Chinese with English abstract) DOI: 10.3969/j.issn.1000-3665.2007.03.024 [4] 王雷, 吴君平, 赵冰雪, 等. 基于GIS和信息量模型的安徽池州地质灾害易发性评价[J]. 中国地质灾害与防治学报,2020,31(3):96 − 103. [WANG Lei, WU Junping, ZHAO Bingxue, et al. Susceptibility assessment of geohazards in Chizhou City of Anhui Province based on GIS and informative model[J]. The Chinese Journal of Geological Hazard and Control,2020,31(3):96 − 103. (in Chinese with English abstract) [5] 李益敏, 李驭豪, 赵志芳. 基于确定性系数模型的泸水市泥石流易发性评价[J]. 水土保持研究,2019,26(4):336 − 342. [LI Yimin, LI Yuhao, ZHAO Zhifang. Assessment on susceptibility of debris flow in Lushui based on the certain factor model[J]. Research of Soil and Water Conservation,2019,26(4):336 − 342. (in Chinese with English abstract) [6] 胡燕, 李德营, 孟颂颂, 等. 基于证据权法的巴东县城滑坡灾害易发性评价[J]. 地质科技通报,2020,39(3):187 − 194. [HU Yan, LI Deying, MENG Songsong, et al. Landslide susceptibility evaluation in Badong County based on weights of evidence method[J]. Bulletin of Geological Science and Technology,2020,39(3):187 − 194. (in Chinese with English abstract) [7] 任敬, 范宣梅, 赵程, 等. 贵州省都匀市滑坡易发性评价研究[J]. 水文地质工程地质,2018,45(5):165 − 172. [REN Jing, FAN Xuanmei, ZHAO Cheng, et al. Evaluation of the landslide vulnerability in Duyun of Guizhou Province[J]. Hydrogeology & Engineering Geology,2018,45(5):165 − 172. (in Chinese with English abstract) [8] 牛瑞卿, 彭令, 叶润青, 等. 基于粗糙集的支持向量机滑坡易发性评价[J]. 吉林大学学报(地球科学版),2012,42(2):430 − 439. [NIU Ruiqing, PENG Ling, YE Runqing, et al. Landslide susceptibility assessment based on rough sets and support vector machine[J]. Journal of Jilin University (Earth Science Edition),2012,42(2):430 − 439. (in Chinese with English abstract) [9] 杨永刚, 殷坤龙, 赵海燕, 等. 基于C5.0决策树-快速聚类模型的万州区库岸段乡镇滑坡易发性区划[J]. 地质科技情报,2019,38(6):189 − 197. [YANG Yonggang, YIN Kunlong, ZHAO Haiyan, et al. Landslide susceptibility evaluation for township units of bank section in Wanzhou district based on C5.0 decision tree and K-means cluster model[J]. Geological Science and Technology Information,2019,38(6):189 − 197. (in Chinese with English abstract) [10] 刘睿, 施婌娴, 孙德亮, 等. 基于GIS与随机森林的巫山县滑坡易发性区划[J]. 重庆师范大学学报(自然科学版),2020,37(3):86 − 96. [LIU Rui, SHI Shuxian, SUN Deliang, et al. Based on GIS and random forest model for landslide susceptibility mapping in Wushan County[J]. Journal of Chongqing Normal University (Natural Science),2020,37(3):86 − 96. (in Chinese with English abstract) [11] 周超, 殷坤龙, 曹颖, 等. 基于集成学习与径向基神经网络耦合模型的三峡库区滑坡易发性评价[J]. 地球科学,2020,45(6):1865 − 1876. [ZHOU Chao, YIN Kunlong, CAO Ying, et al. Landslide susceptibility assessment by applying the coupling method of radial basis neural network and adaboost: a case study from the Three Gorges reservoir area[J]. Earth Science,2020,45(6):1865 − 1876. (in Chinese with English abstract) [12] 杨光, 徐佩华, 曹琛, 等. 基于确定性系数组合模型的区域滑坡敏感性评价[J]. 工程地质学报,2019,27(5):1153 − 1163. [YANG Guang, XU Peihua, CAO Chen, et al. Assessment of regional landslide susceptibility based on combined model of certainty factor method[J]. Journal of Engineering Geology,2019,27(5):1153 − 1163. (in Chinese with English abstract) [13] 李文彦, 王喜乐. 频率比与信息量模型在黄土沟壑区滑坡易发性评价中的应用与比较[J]. 自然灾害学报,2020,29(4):213 − 220. [LI Wenyan, WANG Xile. Application and comparison of frequency ratio and information value model for evaluating landslide susceptibility of loess gully region[J]. Journal of Natural Disasters,2020,29(4):213 − 220. (in Chinese with English abstract) [14] 黄发明, 叶舟, 姚池, 等. 滑坡易发性预测不确定性: 环境因子不同属性区间划分和不同数据驱动模型的影响[J]. 地球科学,2020,45(12):4535 − 4549. [HUANG Faming, YE Zhou, YAO Chi, et al. Uncertainties of landslide susceptibility prediction: Different attribute interval divisions of environmental factors and different data-based models[J]. Earth Science,2020,45(12):4535 − 4549. (in Chinese with English abstract) [15] MERSHA T, METEN M. GIS-based landslide susceptibility mapping and assessment using bivariate statistical methods in Simada area, northwestern Ethiopia[J]. Geoenvironmental Disasters,2020,7:20. DOI: 10.1186/s40677-020-00155-x
[16] 马思远, 许冲, 田颖颖, 等. 基于逻辑回归模型的九寨沟地震滑坡危险性评估[J]. 地震地质,2019,41(1):162 − 177. [MA Siyuan, XU Chong, TIAN Yingying, et al. Application of logistic regression model for hazard assessment of earthquake-triggered landslides: A case study of 2017 Jiuzhaigou(China) Ms7.0 event[J]. Seismology and Geology,2019,41(1):162 − 177. (in Chinese with English abstract) DOI: 10.3969/j.issn.0253-4967.2019.01.011 [17] 王进, 郭靖, 王卫东, 等. 权重线性组合与逻辑回归模型在滑坡易发性区划中的应用与比较[J]. 中南大学学报(自然科学版),2012,43(5):1932 − 1939. [WANG Jin, GUO Jing, WANG Weidong, et al. Application and comparison of weighted linear combination model and logistic regression model in landslide susceptibility mapping[J]. Journal of Central South University (Science and Technology),2012,43(5):1932 − 1939. (in Chinese with English abstract) [18] 邓念东, 石辉, 文强, 等. 信息量支持下的随机森林模型的崩塌易发性评价[J]. 科学技术与工程,2021,21(6):2210 − 2217. [DENG Niandong, SHI Hui, WEN Qiang, et al. Collapse susceptibility evaluation of random forest model supported by information value model[J]. Science Technology and Engineering,2021,21(6):2210 − 2217. (in Chinese with English abstract) DOI: 10.3969/j.issn.1671-1815.2021.06.012 [19] 蒋德明, 李益敏, 鲍华姝. 泸水县滑坡孕灾环境因素敏感性研究[J]. 自然灾害学报,2016,25(4):109 − 119. [JIANG Deming, LI Yimin, BAO Huashu. Study on sensitivity in disaster-pregnant environmental factors of landslide in Lushui County[J]. Journal of Natural Disasters,2016,25(4):109 − 119. (in Chinese with English abstract) [20] 吴森, 李虎杰, 陈国辉, 等. 基于贡献率权重法的区域滑坡影响因子敏感性分析[J]. 中国地质灾害与防治学报,2016,27(1):26 − 31. [WU Sen, LI Hujie, CHEN Guohui, et al. Regional landslides influence factors sensitivity analysis based on contributing weight method[J]. The Chinese Journal of Geological Hazard and Control,2016,27(1):26 − 31. (in Chinese with English abstract) [21] 王佳佳, 殷坤龙, 肖莉丽. 基于GIS和信息量的滑坡灾害易发性评价: 以三峡库区万州区为例[J]. 岩石力学与工程学报,2014,33(4):797 − 808. [WANG Jiajia, YIN Kunlong, XIAO Lili. Landslide susceptibility assessment based on GIS and weighted information value: A case study of Wanzhou district, Three Gorges Reservoir[J]. Chinese Journal of Rock Mechanics and Engineering,2014,33(4):797 − 808. (in Chinese with English abstract) [22] 张玘恺, 凌斯祥, 李晓宁, 等. 九寨沟县滑坡灾害易发性快速评估模型对比研究[J]. 岩石力学与工程学报,2020,39(8):1595 − 1610. [ZHANG Qikai, LING Sixiang, LI Xiaoning, et al. Comparison of landslide susceptibility mapping rapid assessment models in Jiuzhaigou County, Sichuan Province, China[J]. Chinese Journal of Rock Mechanics and Engineering,2020,39(8):1595 − 1610. (in Chinese with English abstract) [23] 孙小凡, 张鹏, 党超. 基于GIS的城市滑坡灾害易发性评价: 以湖北省宜昌市城区为例[J]. 水土保持通报,2018,38(6):304 − 309. [SUN Xiaofan, ZHANG Peng, DANG Chao. Landslide proneness evaluation based on GIS platform in urban area of Yichang City, Hubei Province[J]. Bulletin of Soil and Water Conservation,2018,38(6):304 − 309. (in Chinese with English abstract) [24] 倪树斌, 马超, 杨海龙, 等. 北京山区崩塌、滑坡、泥石流灾害空间分布及其敏感性分析[J]. 北京林业大学学报,2018,40(6):81 − 91. [NI Shubin, MA Chao, YANG Hailong, et al. Spatial distribution and susceptibility analysis of avalanche, landslide and debris flow in Beijing Mountain region[J]. Journal of Beijing Forestry University,2018,40(6):81 − 91. (in Chinese with English abstract) [25] 杜晓晨, 陈莉, 陈廷芳. 基于GIS的凉山州德昌县滑坡危险性评价[J]. 长江流域资源与环境,2020,29(5):1206 − 1215. [DU Xiaochen, CHEN Li, CHEN Tingfang. Hazard assessment of landslide in Dechang County of Liangshan state based on GIS[J]. Resources and Environment in the Yangtze Basin,2020,29(5):1206 − 1215. (in Chinese with English abstract) [26] 梁丽萍, 刘延国, 唐自豪, 等. 基于加权信息量的地质灾害易发性评价—以四川省泸定县为例[J]. 水土保持通报,2019,39(6):176 − 182. [LIANG Liping, LIU Yanguo, TANG Zihao, et al. Geologic hazards susceptibility assessment based on weighted information value: A case study in Luding County, Sichuan Province[J]. Bulletin of Soil and Water Conservation,2019,39(6):176 − 182. (in Chinese with English abstract) [27] 杜谦, 范文, 李凯, 等. 二元Logistic回归和信息量模型在地质灾害分区中的应用[J]. 灾害学,2017,32(2):220 − 226. [DU Qian, FAN Wen, LI Kai, et al. Geohazard susceptibility assessment by using binary logical regression and information value model[J]. Journal of Catastrophology,2017,32(2):220 − 226. (in Chinese with English abstract) DOI: 10.3969/j.issn.1000-811X.2017.02.039 [28] 栗泽桐, 王涛, 周杨, 等. 基于信息量、逻辑回归及其耦合模型的滑坡易发性评估研究—以青海沙塘川流域为例[J]. 现代地质,2019,33(1):235 − 245. [LI Zetong, WANG Tao, ZHOU Yang, et al. Landslide susceptibility assessment based on information value model, logistic regression model and their integrated model: A case in Shatang River Basin, Qinghai Province[J]. Geoscience,2019,33(1):235 − 245. (in Chinese with English abstract) -
期刊类型引用(32)
1. 陈玉波,徐世光,陈梦瑞. 以确定性系数法为基础的不同滑坡易发性评价模型对比分析——以云南保山盆地为例. 中国地质灾害与防治学报. 2025(01): 119-130 .  本站查看
本站查看
2. 黄海,江思义,李海良,李春玲,吴秋菊. 岩溶地区危岩和岩质崩塌易发性评价研究——以广西贺州市平桂区为例. 成都理工大学学报(自然科学版). 2024(01): 137-151 .  百度学术
百度学术
3. 申玉松,张宸,王艺杰,张迪. 基于CF-LR模型的河南省信阳市地质灾害易发性评价. 地质与资源. 2024(01): 74-81+134 .  百度学术
百度学术
4. 陈宾,魏娜,张联志,李颖懿,刘宁,屈添强. 基于斜坡单元灾害强度的滑坡灾害易损性评价——以湖南省湘乡市为例. 中国地质灾害与防治学报. 2024(02): 137-145 .  本站查看
本站查看
5. 何卿,简季. 基于信息量模型与确定性系数模型的曩宋河流域地质灾害易发性评价. 自然资源信息化. 2024(01): 56-63 .  百度学术
百度学术
6. 周修波,李永红,何意平,张辉,孙遥,蒙晓,丁子昂. 陕南山区斜坡孕灾地质环境条件分析——以汉阴县漩涡镇为例. 地质灾害与环境保护. 2024(02): 27-35 .  百度学术
百度学术
7. 吴兴贵,王宇栋,王蓝婷,丁梓逸. 加权信息量模型在云南澜沧县滑坡危险性评价中的应用. 中国地质灾害与防治学报. 2024(03): 119-128 .  本站查看
本站查看
8. 关艳丽,贾荣谷,李育红,翁彦梅,李家艳,冯蕊. 水库滑坡机理及风险评价研究与展望. 人民珠江. 2024(08): 10-18 .  百度学术
百度学术
9. 张宇,简季,郝利娜,杨鑫. 基于IV-MLP耦合模型的龙陵县滑坡易发性评价. 物探化探计算技术. 2024(05): 618-626 .  百度学术
百度学术
10. 皮茂强,肖欣,赵毅,梁锋,张坤,蒲云贵. 基于加权信息量模型的遵义市地质灾害易发性评价. 地质灾害与环境保护. 2024(03): 45-54 .  百度学术
百度学术
11. 黄煜,谢婉丽,刘琦琦,杨惠,朱荣森,李嘉昊,穆柯,严明,肖金存,何高锐. 基于GIS与MaxEnt模型的滑坡易发性评价——以铜川市中部城区为例. 西北地质. 2023(01): 266-275 .  百度学术
百度学术
12. 陈芯宇,师芸,温永啸,史瑞遥,米晓梅. 基于确定性系数与支持向量机的滑坡易发性评价. 科学技术与工程. 2023(02): 518-527 .  百度学术
百度学术
13. 支泽民,刘峰贵,周强,夏兴生,陈琼. 基于流域单元的地质灾害易发性评价——以西藏昌都市为例. 中国地质灾害与防治学报. 2023(01): 139-150 .  本站查看
本站查看
14. 张二阳,袁航. 基于信息量模型的上饶市广丰区地质灾害易发性评价. 资源信息与工程. 2023(02): 54-59 .  百度学术
百度学术
15. 王成楠,吴琳伟,宋勇,贺婷,王彪,赵影,胡旭东. 江西省寻乌县滑坡易发性评价模型及精度对比研究. 资源环境与工程. 2023(02): 171-182 .  百度学术
百度学术
16. 邵大江,叶辉,王金亮,周京春,角媛梅,沙晋明. 基于机器学习均值化的地质灾害易发性评价. 云南大学学报(自然科学版). 2023(03): 653-665 .  百度学术
百度学术
17. 何万才,赵俊三,林伊琳,陈国平,李坤,姚皖路. 基于证据权和支持向量机模型的威信县滑坡易发性评价. 科学技术与工程. 2023(15): 6350-6360 .  百度学术
百度学术
18. 牟家琦,庄建琦,王世宝,孔嘉旭,杜晨辉. 基于深度神经网络模型的雅安市滑坡易发性评价. 中国地质灾害与防治学报. 2023(03): 157-168 .  本站查看
本站查看
19. 余芳瑞,王宏卫,钱田田,谢玲,魏一鸣. 地质灾害敏感性下的伊犁河谷生态安全格局构建. 华侨大学学报(自然科学版). 2023(04): 510-517 .  百度学术
百度学术
20. 刘宝生,陈刚,程刚建. 江苏南京地质灾害风险评价. 中国地质灾害与防治学报. 2023(04): 97-104 .  本站查看
本站查看
21. 周苏华,付宇航,邢静康,彭爱泉,蒋明奕. 基于不同统计模型的肯尼亚滑坡危险性评价. 中国地质灾害与防治学报. 2023(04): 114-124 .  本站查看
本站查看
22. 刘帅,朱杰勇,杨得虎,马博. 基于斜坡单元与随机森林模型的元阳县崩滑地质灾害易发性评价. 中国地质灾害与防治学报. 2023(04): 144-150 .  本站查看
本站查看
23. 刘中楠,高银梅,姜河,黄勇炜,丁华栋,颜智强. 基于CF模型的斜坡地质灾害孕灾因子敏感性分析——以湖南省新宁县为例. 中国地质调查. 2023(04): 107-115 .  百度学术
百度学术
24. 王鑫,王鲜,郝业,胡鹏,韩秀清,李博文,杨亚洲. 基于加权信息量法与综合指数法的西安市蒋村街道地质灾害易发性评价对比. 世界地质. 2023(02): 399-408 .  百度学术
百度学术
25. 阳清青,余秋兵,张廷斌,易桂花,张恺. 基于GDIV模型的大渡河中游地区滑坡危险性评价与区划. 中国地质灾害与防治学报. 2023(05): 130-140 .  本站查看
本站查看
26. 王美华. 基于信息量、信息量-逻辑回归模型综合法的地质灾害易发性研究——以诸暨市马剑镇为例. 化工矿产地质. 2023(04): 347-358 .  百度学术
百度学术
27. 薛兴太,葛再洋,强秋平. 基于GIS和综合指数法的地质灾害易发性评价——以安徽省滁州市来安县丘陵区为例. 安徽地质. 2023(04): 307-310 .  百度学术
百度学术
28. 张云波,曾磊,付弘流,张钟远. 基于信息量模型法的石阡县地质灾害易发性评价. 地质灾害与环境保护. 2022(01): 44-49 .  百度学术
百度学术
29. 葛宗旭,刘汉湖,陈行. 丽江市古城区地质灾害易发性评价方法对比. 云南地理环境研究. 2022(03): 69-76 .  百度学术
百度学术
30. 简鹏,李文彦,张治家,时伟,党发宁,郭红东,李松. 基于多因素加权指数和法的区域地质灾害易发性评价研究——以麦积区为例. 甘肃地质. 2022(03): 63-72 .  百度学术
百度学术
31. 毕结昂,徐佩华,宋盛渊,丁锐. 基于信息量-逻辑回归耦合模型的玛纳斯河流域地质灾害易发性评价. 工程地质学报. 2022(05): 1549-1560 .  百度学术
百度学术
32. 史忠鑫,王振海,车增光,张丽. 基于信息量法的江苏盱眙第一山地质灾害易发性评价. 上海国土资源. 2022(04): 56-60+120 .  百度学术
百度学术
其他类型引用(12)




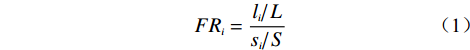
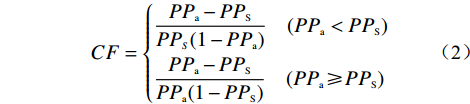
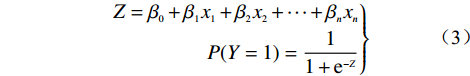

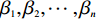
 下载:
下载:

 邮件订阅
邮件订阅 RSS
RSS