Primary establishment of an early warning model of debris flow hazards in Nyingchi City of Tibetan autonomous region based on raster runoff simulation
-
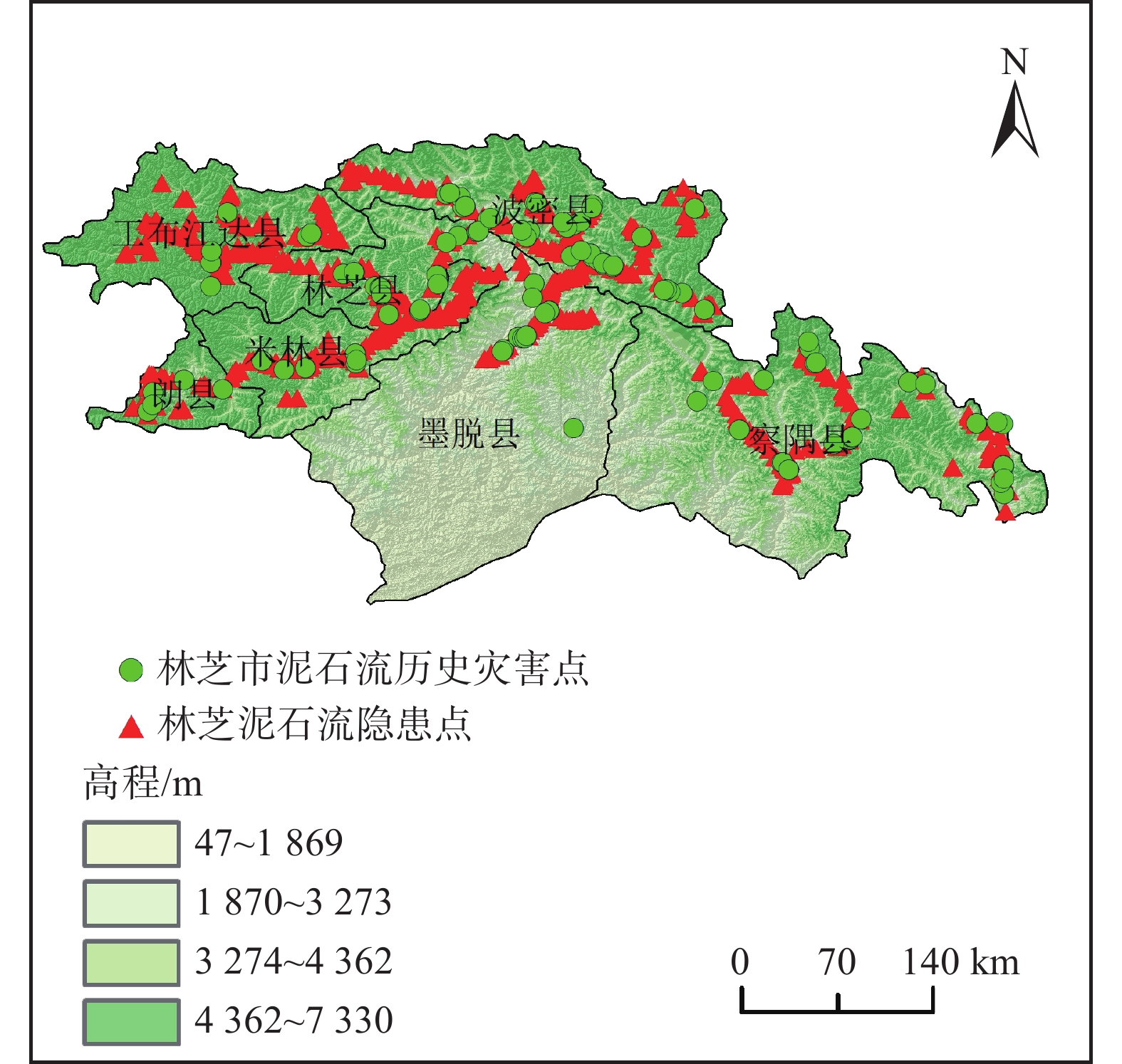
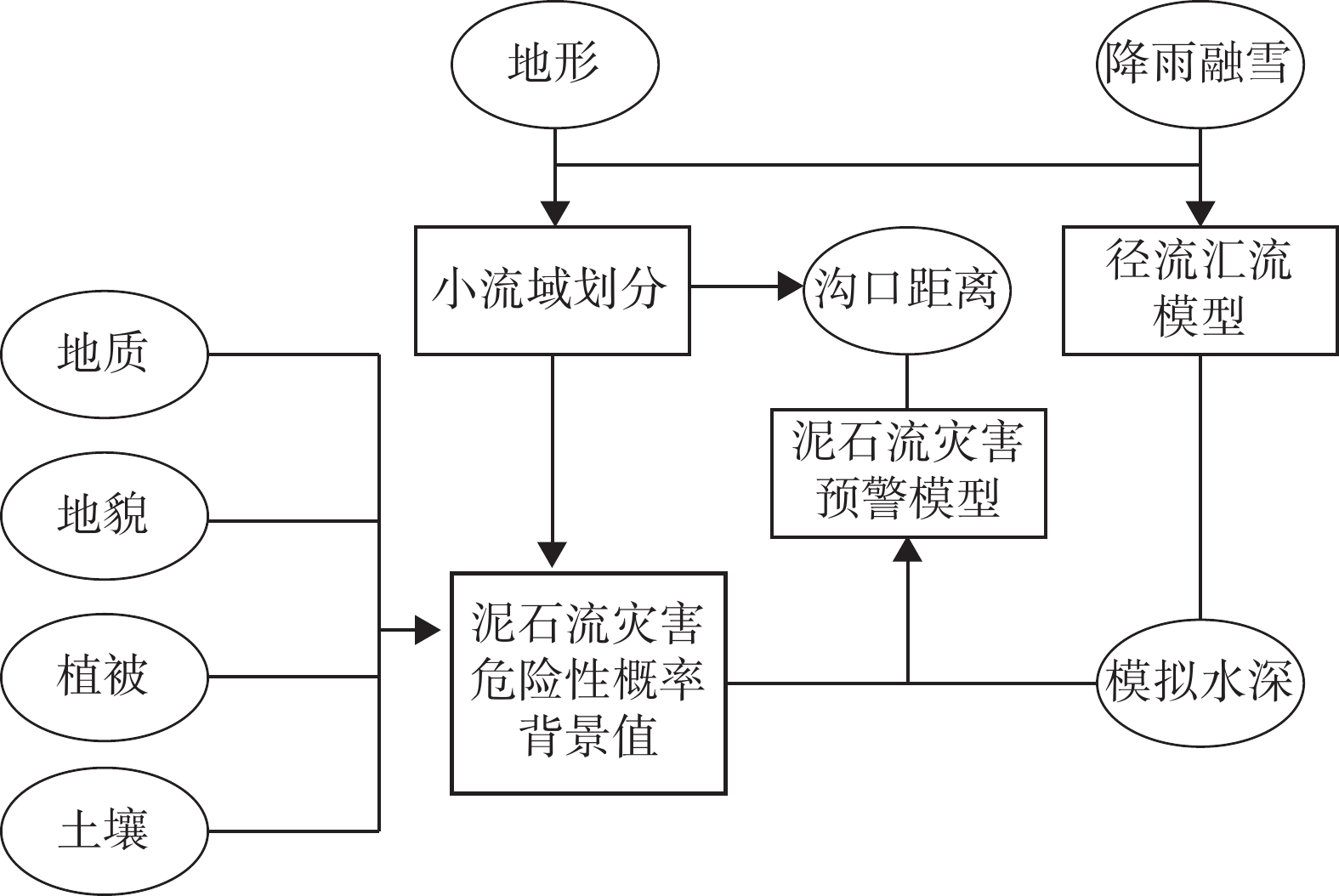
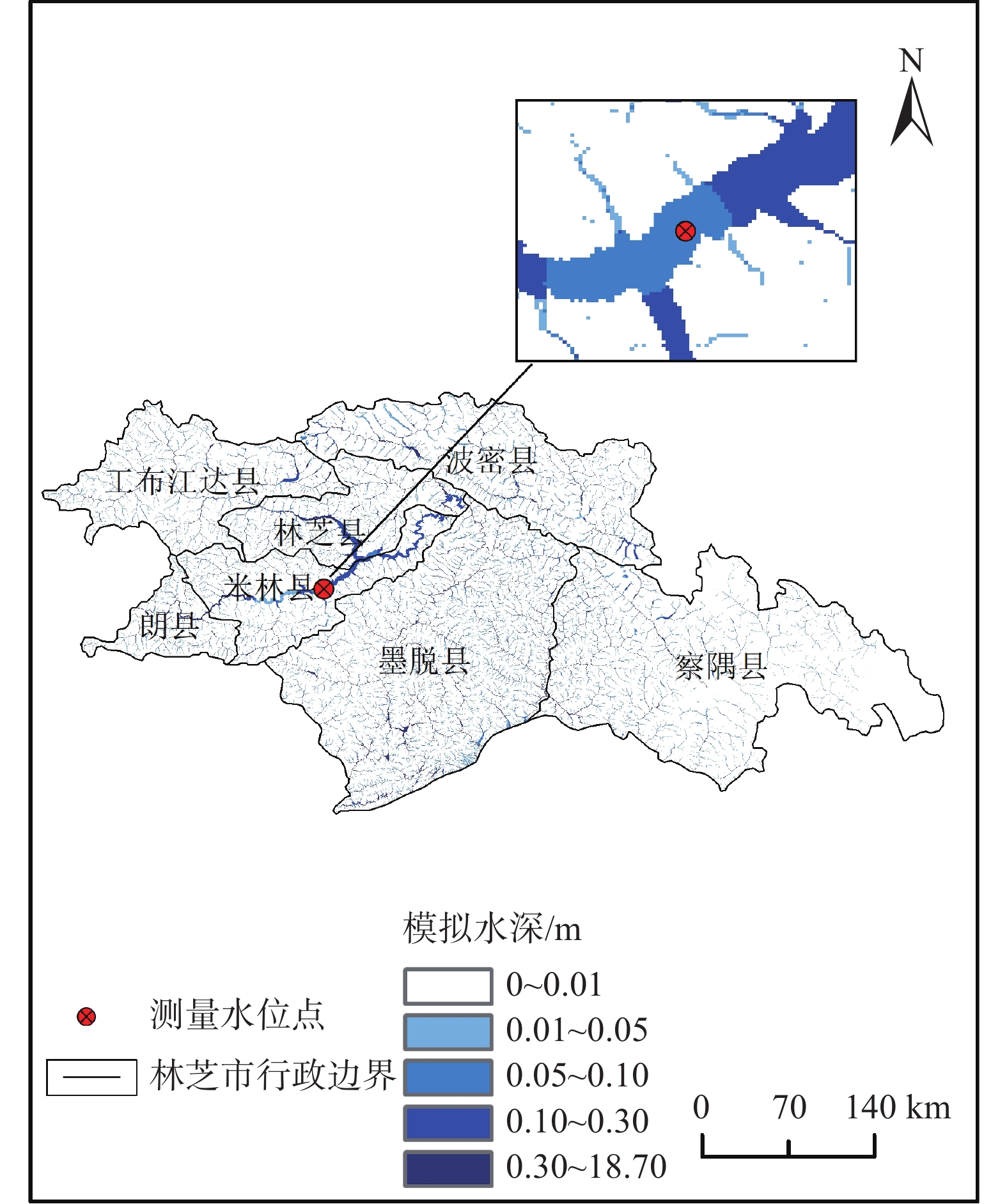
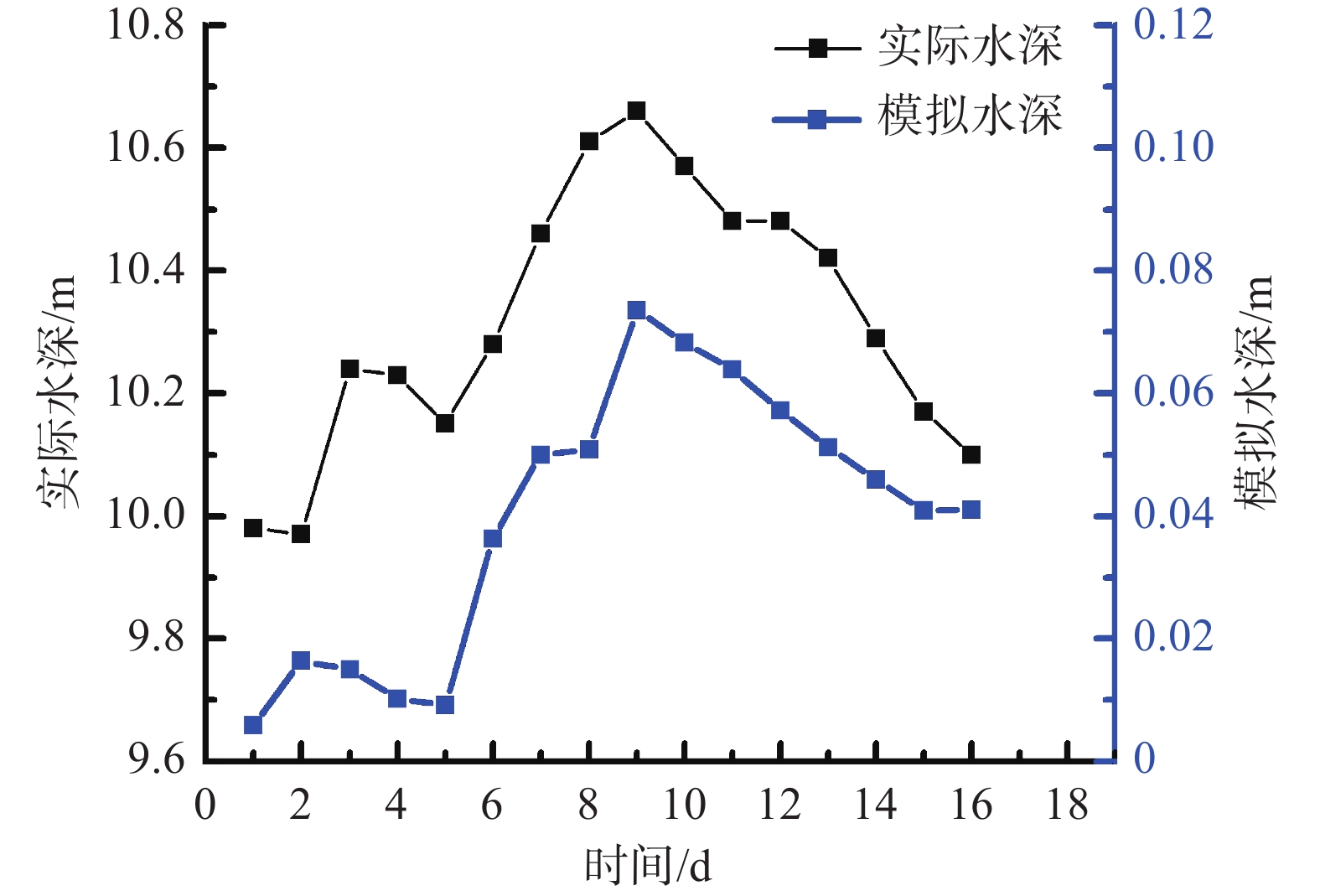
摘要: 西藏林芝市泥石流灾害频发，亟需建立泥石流灾害预警模型，预测林芝市泥石流灾害可能发生的区域，减少泥石流灾害导致的损失。文章提出了一种基于栅格径流汇流的林芝市泥石流灾害预警模型，从栅格像元尺度上模拟流域各位置上的水深，以提高泥石流预警的空间针对性。该模型将泥石流致灾因子分为背景因子和激发因子。通过林芝市裸岩率、河床纵比降等因子的逻辑回归，获取林芝市泥石流灾害概率，作为泥石流预警模型的背景因子；引入栅格径流汇流模型，以站点降水和雪水当量为模型的水量输入，模拟预警时段内的流域各位置上的模型水深，作为泥石流预警模型的激发因子。利用二元逻辑回归的方法计算背景因子和激发因子的权重，建立泥石流预警模型。利用2011—2020年18次历史灾害对模型进行验证，落入预警区内的灾害点占比64.4%，预警精度较高，对于林芝市泥石流灾害预警具有一定的指导意义。Abstract: Debris flow disasters occur frequently in Nyingchi City, Tibet. There is an urgent need to establish an early warning model to predict the possible areas of debris flow disasters in Nyingchi City and reduce the losses caused by those disasters. This paper presented an early warning model based on raster runoff simulation in Nyingchi City, which can simulate the water depth at each location in the watershed and improve the spatial pertinence of debris flow early warning. In this model, the disaster factors of debris flow are divided into background factor and excitation factor. The probability of debris flow disaster in Nyingchi City is obtained by logistic regression of many factors such as bare rock rate, vertical slope of riverbed and so on, which is used as the background factor. The raster runoff simulation model is introduced to simulate the predicted water depth at each position of the basin during the early warning period by importing the precipitation and snow water equivalent data. Using binary logistic regression method to calculate the weight of background factor and excitation factor, the final model is obtained. 18 historical disasters from 2011 to 2020 were used to verify the model. The disaster points falling into the early warning area accounted for 64.4%, which has certain guiding significance for the early warning of debris flow disaster in Nyingchi City.
-
Keywords:
- Nyingchi City /
- debris flow disaster /
- runoff simulation
-
0. 引言
查明与地质灾害有关的危险区域是地质灾害管理的重要工作，也是促进研究区人民生活和基础设施发展安全的重要依据[1]，基于建模评价地质灾害易发性是重要而且有效的途径。
应用经验式、数值模拟和统计方法对地质灾害易发性建模和评价，已经进行了许多研究[1-10]。其中，经验式方法基于现场观察和专家经验判断；数值模拟计算边坡的稳定性；统计方法部分基于实地观察和专家的先验知识，部分基于对地质灾害发生的权重或概率的统计计算，这类方法使用统计技术来评估诱发地质灾害的各种因素的相关作用，每个因素的重要性都是根据观察到的与地质灾害的关系来确定的。
文中使用基于贝叶斯理论的证据权法，综合GIS技术评价研究区地质灾害易发性。证据权法是一种统计方法，最初应用于非空间、定量的医学诊断，以结合临床诊断的证据来预测疾病[11-12]。在地球科学中，该方法被广泛应用，如：矿产资源潜力评估和矿床预测[13-16]，公路路基岩溶塌陷危险性评价[17]和滑坡易发性和危险性[1, 3, 18-23]。
1. 研究区和数据
1.1 研究区概况
文中选择云南高原滇中昆明盆地低山丘陵地带这一云南省地质灾害防治重点地区的典型代表，云南省省会昆明市的主要行政区之一，昆明市五华区作为研究对象，该区地质灾害易发性评价研究具有典型代表性，可向整个云南高原昆明盆地低山丘陵区和其他低山丘陵区推广，具有技术方法和社会经济意义。研究区面积381.6 km2，地势西北高东南低，昆明盆地内地形开阔低缓，北部山区地形崎岖，沟壑较发育。区域年降水量的80%以上集中在6—9月，年平均降水量608.4～887.0 mm。碳酸盐岩分布最广，约占全区面积的38.93%，其次为砂岩、泥岩、页岩，约占23.11%，岩浆岩主要为玄武岩，约占16.95%，主要分布在昆明盆地和其他小盆地的松散碎石土体约占11.36%，石英砂岩类约占7.56%，还发育一些岩脉；断裂构造较发育，以南北向构造为主[24-25]。
1.2 数据收集
通过地质灾害风险普查获得了研究区地质灾害分布数据。根据调查分析，选择工程地质岩组、断裂构造、高程、坡度、坡向、坡面曲率、距公路距离和土地利用类型等8类因素纳入评价分析。地质数据收集自云南省地质局1∶20万昆明幅、武定幅区域地质调查报告和图件[24-25]，12.5 m分辨率DEM（数字高程模型）收集自ASF，道路数据收集自OSM，土地利用类型数据收集自ESA（图1、表1）。
表 1 数据简介Table 1. Data introduction数据 灾点及
致灾要素类型 来源 地灾 地灾点 矢量点 地质灾害风险普查 地质 工程地质岩组 矢量面 云南省地质局 距断裂
距离矢量线和缓冲区 云南省地质局 地形地貌 高程 栅格 12.5 m DEM，
https://asf.alaska.edu/坡度 栅格 根据DEM，应用ArcGIS提取 坡向 栅格 根据DEM，应用ArcGIS提取 坡面曲率 栅格 根据DEM，应用ArcGIS提取 道路 距公路
距离矢量线缓冲区 http://www.openstreetmap.org，
根据矢量线用ArcGIS制作土地利用
类型土地利用
类型栅格 ESA WorldCover 10 m 2020，https://esa-worldcover.org/en 1.3 地质灾害发育特征
现状发育地质灾害89处，滑坡73处，崩塌11处，泥石流4条，地面沉降1处，为小—中型，无大型，中型14处，小型75处，主要分布在研究区低山丘陵地貌区，盆地内仅发育1处（图2）。
![]()
图 2 地质灾害分布图（底图为高程和山体阴影渲染）Figure 2. Map of geological hazard distribution (The bottom was rendered by elevation and hillshade)选择指标“因子面积百分比A”“地灾数百分比B”和“比率(β=B/A)”表征地质灾害的空间分布特征、主控因素和成灾特征。β定义了地质灾害点在因素分级中相对于均匀分布的丰度，β>1表示相对丰度更高，β<1则相反。β>1的因素分级有（图3、表2）：高程1800～1850 m、1920～1950 m和1950～2000 m，坡度15°～25°、25°～35°和>35°，坡向北东、东、南东和北，坡面曲率−0.75～−0.28（凹形）、−0.28～−0.15（凹形）、−0.15～−0.05(凹形)和0.05～0.15（凸形），石英砂岩岩组和砂岩、泥岩、页岩岩组，距断层距离0～50 m、300～500 m和1000～2000 m，距主要公路距离0～50 m和50～100 m，草地和裸地/稀疏植被区域。这些因素分级内，发育了相对于均匀分布丰度更高的地质灾害，表征这些因素分级可能是研究区地质灾害的主控因素。
![]()
图 3 各因素分级分区和地灾点数量相关性统计图Figure 3. Statistical charts of correlation between the factors and the number of geological hazard points2. 方法
2.1 权重计算
把研究区栅格单元化，利用条件概率计算证据因素图层所有单元对地质灾害发生的贡献权重[13-15, 26-27]。定义
$ D $ 为已发生地质灾害的单元，$ \bar{D} $ 为未发生地质灾害的单元，$ B $ 为证据因素区内的单元，$ \bar{B} $ 为证据因素区外的单元。证据因素
$ B $ 条件下$ D $ 的条件（后验）概率为：$$ { O}\left(D|B\right)={ O}\left(D\right)\frac{P\left(B\right|D)}{P(B|{\bar D})} $$ (1) 式中：
$ { O}\left(D\right) $ —证据因素B的先验概率，${{ O}}\left(D\right)=$ $\dfrac{\mathrm{事}\mathrm{件}\mathrm{将}\mathrm{会}\mathrm{发}\mathrm{生}\mathrm{的}\mathrm{概}\mathrm{率}}{\mathrm{事}\mathrm{件}\mathrm{不}\mathrm{会}\mathrm{发}\mathrm{生}\mathrm{的}\mathrm{概}\mathrm{率}}=\dfrac{P\left(D\right)}{1-P\left(D\right)}=$ $\dfrac{P\left(D\right)}{P({\bar D})} $ ；$P\left(B\right|D)、 P(B|{\bar D})$ ——在地质灾害发生（D）和未发生 （$ \bar{D} $ ）时，证据因素B的条件 概率，取自然对数即是证据 权法中的正权重（证据因素 存在区的权重值）$ {W}^{+} $ 。$$ {W}^+=\ln\frac{P\left(B\right|D)}{P\left(B|{\bar D}\right)} $$ (2) $$ P\left(B|D\right)=P\left(B\cap D\right)/P\left(D\right) $$ (3) $$ P(B|\bar{D})=P(B\cap \bar{D})/P(\bar{D}) $$ (4) 用
$ D $ 和$ B $ 的单元数N可表示为：$$ P\left(B|D\right)=N\left(B\cap D\right)/N\left(D\right) $$ (5) $$ P(B|\bar{D})=N(B\cap \bar{D})/N(\bar{D}) $$ (6) 同式（1），在证据因素不存在的情况下（
$ \bar{B} $ ），$ D $ 的条件概率（后验）为：$$ {{ O}}(D|\bar{B})={{ O}}(D)\frac{P(\bar{B}|D)}{P(\bar{B}|\bar{D})} $$ (7) 式中：
$P(\bar{B}|D)/P(\bar{B}|\bar{D})$ —取自然对数即是负权重（证据 因素不存在区的权重值）$ {W}^{-} $ 。$$ {W}^-={\rm{ln}}\frac{P(\bar{B}|D)}{P(\bar{B}|\bar{D})} $$ (8) 同式（3）—（6）：
$$ P(\bar{B}|D)=N(\bar{B}\cap D)/N(D) $$ (9) $$ P(\bar{B}|\bar{D})=N(\bar{B}\cap \bar{D})/N(\bar{D}) $$ (10) $N (B\cap D) + N (\bar{B}\cap D)=N(D)$ ，$N (B\cap \bar{D}) + N (\bar{B}\cap \bar{D})= N(\bar{D})$ ，所以式（2）和式（8）可写为：$$ {W}^+={\rm{ln}}\left(\frac{N(B\cap D)}{N(B\cap D)+N(\bar{B}\cap D)}/\frac{N(B\cap \bar{D})}{N(B\cap \bar{D})+N(\bar{B}\cap \bar{D})}\right) $$ (11) $$ {W}^-={\rm{ln}}\left(\frac{N(\bar{B}\cap D)}{N(B\cap D)+N(\bar{B}\cap D)}/\frac{N(\bar{B}\cap \bar{D})}{N(B\cap \bar{D})+N(\bar{B}\cap \bar{D})}\right) $$ (12) 根据式（11）和（12），使用ArcGIS空间分析工具执行权重
$ {W}^{+} $ 和$ {W}^{-} $ 计算。$ {W}^{+} $ 的大小表明证据因素的存在与地质灾害发生之间存在正相关关系。$ {W}^{-} $ 表示负相关，即证据因素存在抑制诱发地质灾害的作用。证据因素原始数据缺失区域的权重值取0。两个权重之间的差异$ {W}_{{\rm{f}}}={W}^{+}-{W}^{-} $ ，即综合权重，量化证据因素和地质灾害相关性大小。如果$ {W}_{{\rm{f}}} $ 为正，则证据因素对地质灾害有利，如果为负，则对滑坡不利。如果$ {W}_{{\rm{f}}} $ 接近于零，则表明证据因素与地质灾害的相关性不大。2.2 因素分级（分类）的显著性测试
在上述权重值计算及分析的基础上，实施证据因素分类的优选，选择类间差异显著的证据因素类，归并不显著的证据因素类。选择近似学生化检验（Student-T）统计值进行显著性测试[15, 28]：
$$ {S tuden{t}}-{{T}}={W}_{{\rm{f}}}/{\sigma }_{{W}_{{\rm{f}}}}={W}_{{\rm{f}}}/\sqrt{{\sigma }_{{W}^+}^{2}+{\sigma }_{{W}^-}^{2}} $$ (13) 式中：
$ {\sigma }_{{W}^{+}}^{} $ 、$ {\sigma }_{{W}^{-}}^{} $ ——分别是$ {W}^{+} $ 和$ {W}^{-} $ 的标准差；Wf ——综合权重；
${\sigma }_{{W}_{{\rm{f}}}}$ ——综合权重标准差。当测试值的绝对值
$|{S tuden{t}}-{ T}|$ 为1.96和2.326时，置信度达97.5%、99%，文中以$|{S tuden{t}}-{ T}|=2$ 作为阈值。先将证据因素划分为若干分级（分类），计算权重和标准差、${{S} tuden{t}}-{ T}$ ，将$|{S} tuden{t}-{ T} | < 2$ 的各分类视为显著性低并归为一类，保留$|{{S} tuden{t}}-{T}|\geqslant 2$ 的因素分类，然后重新计算归并后各分类的权重值。2.3 证据综合
根据贝叶斯法则，任一单元
$ K $ 为地质灾害的可能性，即对数后验概率可表示为[13-15, 26, 27]：$$ F=\ln O\left(D|\sum _{i=1}^{n}{B}_{i}^{K\left(i\right)}\right)=\sum _{i=0}^{n}{W}_{i}^{K}+\ln O\left(D\right) $$ (14) 式中：
$ {B}_{i} $ ——第$ i $ 个证据因素层；$ K\left(i\right) $ —$ {W}_{i} $ 是第$ i $ 个证据因素存在或不存在的权 重，在第$ i $ 个证据因素层存在时是+，不存在 时是−。最后计算后验概率：
$$ P=O/(1+O)=\exp\left(F\right)/\left(1+\exp\left(F\right)\right) $$ (15) 后验概率的大小作为易发性高低的指标，值越大表示易发性越高，值越小表示易发性越低。
3. 结果与讨论
3.1 证据权重计算结果和相关性分析
证据权重计算结果（表2、图4）与1.3节可相互印证。在地形高程方面，1800～1850 m、1920～1950 m和1950～2000 m段利于地质灾害发生，正权重0.5550、1.1758和0.6439。>35°和15°～25°的山体斜坡较易于地质灾害发生，正权重0.5436和0.3785。坡向因素各分级权重值均不高，表明坡向对地质灾害发生的驱动作用可能不太显著。坡面曲率结果显示，−0.75～−0.28（凹形）和−0.28～−0.15（凹形）两个凹形坡分级段较易于地质灾害发生，正权重0.5690和0.7577。工程地质岩组各岩组分类的正权重值总体不高，但砂岩、泥岩、页岩岩组的统计结果仍然表现出对地质灾害发生的较有利性，其正权重0.4474，高于排在第二位的石英砂岩岩组（正权重值为0.2947）。距断层距离和距主要公路距离因素统计结果均显示出了较明显的距离效应，即距断裂或主要公路远的地区与地质灾害发生负相关，距断裂0～50 m和距主要公路0～50 m、50～100 m易于地质灾害发生，其正权重0.7973、0.9820和0.5111。裸地或稀疏植被地区是易于地质灾害发生的区域，其正权重0.8719。
表 2 因素证据权重计算结果表Table 2. Calculation results of factor evidence weights因素 因素分级 因素面积
百分比/%地灾数
百分比/%正权重
W+W+的
标准差${\sigma }_{{W}^{+}}^{} $负权重W− W−的
标准差${\sigma }_{{W}^{-}}^{} $综合权重
$ {W}_{{\rm{f}}} $$ {W}_{{\rm{f}}} $的
标准差${\sigma }_{{W}_{{\rm{f}}}} $Student−T 分类
归并归并后
权重权重
标准差高程/m <1735 0.01 0.00 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 合并 −0.2744 0.1607 1735～1800 0.36 0.00 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 合并 −0.2744 0.1607 1 800～1 850 0.65 1.12 0.5550 1.0082 −0.0048 0.1071 0.5598 1.0138 0.5522 合并 −0.2744 0.1607 1 850～1 900 9.55 10.11 0.0574 0.3350 −0.0063 0.1123 0.0636 0.3533 0.1801 合并 −0.2744 0.1607 1 900～1 920 6.81 4.49 −0.4186 0.5015 0.0248 0.1090 −0.4434 0.5133 −0.8639 合并 −0.2744 0.1607 1 920～1 950 6.73 21.35 1.1758 0.2329 −0.1720 0.1200 1.3478 0.2620 5.1444 4 1.1758 0.2329 1 950～2 000 12.50 23.60 0.6439 0.2202 −0.1368 0.1218 0.7807 0.2516 3.1032 5 0.6439 0.2202 2 000～2 100 23.25 11.24 −0.7318 0.3169 0.1468 0.1131 −0.8787 0.3365 −2.6110 13 −0.7318 0.3169 2 100～2 200 18.86 20.22 0.0708 0.2369 −0.0172 0.1192 0.0879 0.2652 0.3315 合并 −0.2744 0.1607 2 200～2 300 11.48 4.49 −0.9436 0.5009 0.0767 0.1090 −1.0203 0.5126 −1.9903 合并 −0.2744 0.1607 2 300～2 400 7.02 3.37 −0.7383 0.5786 0.0389 0.1084 −0.7772 0.5887 −1.3201 合并 −0.2744 0.1607 2 400～2 500 2.61 0.00 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 合并 −0.2744 0.1607 >2 500 0.19 0.00 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 合并 −0.2744 0.1607 坡度/(°) <5 18.72 4.49 −1.4297 0.5006 0.1620 0.1091 −1.5916 0.5123 −3.1068 5 −1.4297 0.5006 5～15 38.32 37.08 −0.0288 0.1749 0.0174 0.1343 −0.0462 0.2205 −0.2093 合并 0.0221 0.1450 15～25 28.72 41.57 0.3785 0.1655 −0.2023 0.1392 0.5808 0.2163 2.6853 3 0.3785 0.1655 25～35 11.60 12.36 0.0688 0.3030 −0.0093 0.1138 0.0782 0.3237 0.2416 合并 0.0221 0.1450 >35 2.64 4.49 0.5436 0.5040 −0.0195 0.1090 0.5632 0.5157 1.0921 合并 0.0221 0.1450 坡向 北东 9.72 11.24 0.1460 0.3179 −0.0171 0.1130 0.1631 0.3374 0.4833 合并 −0.0001 0.1065 东 12.77 15.73 0.2107 0.2688 −0.0349 0.1160 0.2456 0.2928 0.8388 合并 −0.0001 0.1065 南东 16.92 19.10 0.1222 0.2438 −0.0268 0.1184 0.1490 0.2710 0.5496 合并 −0.0001 0.1065 南 13.16 11.24 −0.1592 0.3175 0.0221 0.1130 −0.1813 0.3370 −0.5379 合并 −0.0001 0.1065 南西 10.57 10.11 −0.0448 0.3348 0.0052 0.1123 −0.0500 0.3532 −0.1415 合并 −0.0001 0.1065 西 13.45 6.74 −0.6954 0.4092 0.0754 0.1103 −0.7707 0.4238 −1.8186 合并 −0.0001 0.1065 北西 14.58 12.36 −0.1667 0.3027 0.0259 0.1138 −0.1926 0.3234 −0.5955 合并 −0.0001 0.1065 北 8.82 13.48 0.4290 0.2908 −0.0529 0.1145 0.4819 0.3125 1.5423 合并 −0.0001 0.1065 坡面
曲率−0.75～−0.28（凹形） 3.20 5.62 0.5690 0.4509 −0.0255 0.1096 0.5945 0.4640 1.2812 合并 0.0960 0.1367 −0.28～−0.15（凹形） 10.64 22.47 0.7577 0.2258 −0.1432 0.1209 0.9009 0.2562 3.5171 1 0.7577 0.2258 −0.15～−0.05（凹形） 19.66 26.97 0.3197 0.2054 −0.0962 0.1246 0.4159 0.2403 1.7311 合并 0.0960 0.1367 −0.05～0.05（平坦） 34.18 16.85 −0.7119 0.2588 0.2362 0.1169 −0.9482 0.2840 −3.3388 6 −0.7119 0.2588 0.05～0.15（凸形） 17.53 21.35 0.1990 0.2307 −0.0478 0.1201 0.2468 0.2601 0.9489 合并 0.0960 0.1367 0.15～0.28（凸形） 11.00 5.62 −0.6766 0.4483 0.0593 0.1097 −0.7359 0.4615 −1.5945 合并 0.0960 0.1367 0.28～0.69（凸形） 3.78 1.12 −1.2194 1.0014 0.0275 0.1071 −1.2469 1.0071 −1.2381 合并 0.0960 0.1367 工程
地质
岩组松散碎石土体 13.15 6.74 −0.6736 0.4092 0.0720 0.1103 −0.7456 0.4238 −1.7592 合并 −0.1844 0.1329 石英砂岩 7.55 10.11 0.2947 0.3354 −0.0283 0.1123 0.3230 0.3537 0.9131 合并 −0.1844 0.1329 砂岩、泥岩、页岩 23.08 35.96 0.4474 0.1781 −0.1844 0.1330 0.6318 0.2222 2.8430 3 0.4474 0.1781 白云岩、灰岩 38.88 37.08 −0.0491 0.1749 0.0301 0.1343 −0.0793 0.2205 −0.3596 合并 −0.1844 0.1329 玄武岩 16.94 10.11 −0.5206 0.3343 0.0800 0.1124 −0.6005 0.3526 −1.7029 合并 −0.1844 0.1329 侵入岩脉 0.29 0.00 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 合并 −0.1844 0.1329 距断层
距离/m0～50 5.63 12.36 0.7973 0.3046 −0.0746 0.1137 0.8719 0.3252 2.6814 3 0.7973 0.3046 50～100 5.86 5.62 −0.0429 0.4492 0.0026 0.1096 −0.0455 0.4624 −0.0985 合并 −0.0746 0.1137 100～300 19.87 19.10 −0.0397 0.2436 0.0096 0.1184 −0.0493 0.2709 −0.1822 合并 −0.0746 0.1137 300～500 16.11 20.22 0.2299 0.2371 −0.0508 0.1192 0.2806 0.2654 1.0574 合并 −0.0746 0.1137 500～1000 26.12 17.98 −0.3764 0.2508 0.1056 0.1177 −0.4820 0.2770 −1.7397 合并 −0.0746 0.1137 1000～2 000 22.75 24.72 0.0840 0.2143 −0.0261 0.1227 0.1101 0.2469 0.4457 合并 −0.0746 0.1137 >2000 3.66 0.00 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 合并 −0.0746 0.1137 距主要
公路
距离/m0～50 11.11 29.21 0.9820 0.1986 −0.2296 0.1265 1.2116 0.2354 5.1469 3 0.9820 0.1986 50～100 8.14 13.48 0.5111 0.2909 −0.0605 0.1145 0.5716 0.3126 1.8284 合并 −0.1257 0.1296 100～300 20.62 20.22 −0.0196 0.2368 0.0050 0.1192 −0.0247 0.2651 −0.0931 合并 −0.1257 0.1296 300～500 12.53 3.37 −1.3195 0.5781 0.1005 0.1084 −1.4201 0.5882 −2.4144 4 −1.3195 0.5781 500～1000 17.21 16.85 −0.0210 0.2594 0.0043 0.1168 −0.0253 0.2845 −0.0889 合并 −0.1257 0.1296 1000～2 000 16.67 10.11 −0.5038 0.3343 0.0765 0.1124 −0.5803 0.3527 −1.6455 合并 −0.1257 0.1296 >2000 13.72 6.74 −0.7153 0.4092 0.0785 0.1103 −0.7939 0.4238 −1.8733 合并 −0.1257 0.1296 土地
利用
类型林地 54.70 28.09 −0.0794 0.1497 0.0883 0.1515 −0.1676 0.2130 −0.7870 合并 −0.1287 0.1183 灌木 0.14 0.00 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 合并 −0.1287 0.1183 草地 7.39 8.99 0.1979 0.3556 −0.0176 0.1116 0.2155 0.3727 0.5783 合并 −0.1287 0.1183 耕地 16.54 10.11 −0.4955 0.3343 0.0749 0.1124 −0.5704 0.3527 −1.6174 合并 −0.1287 0.1183 建筑 12.82 11.24 −0.1332 0.3175 0.0182 0.1130 −0.1514 0.3370 −0.4492 合并 −0.1287 0.1183 裸地或稀疏植被 8.09 41.57 0.8719 0.2452 −0.1287 0.1183 1.0006 0.2723 3.6746 4 0.8719 0.2452 开阔水域 0.32 0.00 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 合并 −0.1287 0.1183 3.2 模型ROC曲线和AUC
采用接受者操作特性曲线（Receiver Operating Characteristic Curve，ROC）和ROC 曲线下与坐标轴围成的面积（Area Under Curve，AUC）[29-32]评估模型拟合精度。模型拟合精度越好则AUC越接近1，0.7～0.9时表示较好。文中建立的证据权法模型的AUC为80.4%，拟合精度优异（图5）。
3.3 易发性评价结果
综合自然间断点分级和地质灾害分布，圈定了高易发区、中易发区和低易发区（表3、图6），其中高易发区188.55 km2（占研究区总面积的49.41%），中易发区152.21 km2（占研究区总面积的39.88%），89.9%和9.1%的地灾点落入高易发区和中易发区，显示易发性分区符合已发地质灾害分布，模型预测性能较好。
表 3 地质灾害易发性分区表Table 3. Form of geological hazard susceptibility zoning易发性
分区面积/
km2占总面积/
%编号 面积/
km2占大区/
面积%灾点数 灾点密度/
(个·km−2)地质灾害
高易发区（Ⅰ）188.55 49.41 Ⅰ1 152.32 80.79 64 0.41 Ⅰ2 17.93 9.51 9 0.50 Ⅰ3 16.11 8.54 8 0.94 Ⅰ4 2.19 1.16 1 0.46 地质灾害
中易发区（Ⅱ）152.21 39.88 Ⅱ1 1.30 0.85 − − Ⅱ2 18.82 12.36 2 0.11 Ⅱ3 15.03 9.87 1 0.07 Ⅱ4 12.92 8.49 − − Ⅱ5 18.51 12.16 2 0.11 Ⅱ6 9.12 5.99 − − Ⅱ7 44.66 29.34 − − Ⅱ8 12.34 8.11 1 0.08 Ⅱ9 11.73 7.71 − − Ⅱ10 7.78 5.11 − − 低易发区（Ⅲ） 47.40 12.42 Ⅲ1 47.40 100 1 0.02 结合地质环境因素特征分析西部高易发区（图6蓝色框范围内、图7）主要位于砂岩、泥岩和页岩岩组，断裂构造较密集，以山谷斜坡地貌为主，坡度15°～25°和>35°较陡峭斜坡范围成片发育且面积较广，主要公路建于本区山谷，裸地/稀疏植被和草地连片覆盖范围较大。预测圈定的高易发区的这些分布特征，与上文分析得到的地质灾害控制因素特征吻合，预测结果符合地质灾害空间分布特征。
4. 结论
（1）“因子面积百分比A”“地灾数百分比B”和“比率β”，以及各因素各分类地质灾害证据权重可以定量地分析各因素与地质灾害发生的相关性。
（2）圈定高易发区188.55 km2（占总面积的49.41%），中易发区152.21 km2（占总面积的39.88%），易发性分区图具有较好的等级区分度。
（3）通过证据权法绘制的地质灾害易发性图可以有效地预测该区地质灾害，模型拟合精度AUC=80.4%。89.9%和9.1%的地灾点落入高和中易发区，建模结果与实际地质灾害发育情况吻合度高，较好地揭示了研究区地质灾害易发性特征。
（4）证据权法在研究区这类云南高原低山丘陵区有效性高，方法理论清晰，较为成熟，由数据驱动，参数定义明确，易于一线工程师推广使用。同时，该方法权重的估计和模型预测性能受预测因子选择、因子数据空间分辨率、因子分级影响较大，具体工作中宜对这些问题进行深入研究和统计分析。建议通过对因子分级进行显著性测试实施优选，减小对权重的高估或低估，提高模型效能。
-
![]()
图 1 林芝市泥石流灾害点、隐患点分布图
Figure 1. Distribution of debris flow disaster sites and hidden danger points in Nyingchi City
![]()
图 4 2015年9月6日23时径流汇流模拟结果
Figure 4. Results of runoff simulation at 23:00 on September 6, 2015
![]()
图 5 测量水位点模拟水深与实际水深对比
Figure 5. Comparison between simulated water depth and actual water depth at measured water level sites
![]()
图 6 林芝市泥石流历史灾害点河道距离
Figure 6. The distance of river course of historical disaster site of debris flow in Nyingchi City
![]()
图 7 不同预警阈值下的预警区灾害点比例和平均预警区面积平均占比
Figure 7. Proportion of disaster sites in early warning area and average proportion of average early warning area under different early warning thresholds
![]()
图 8 林芝市2020年7月11日、8月15日泥石流灾害预警图
Figure 8. Debris flow disaster warning map of Nyinginzhi on July 11、August 15, 2020
表 1 逻辑回归分析结果
Table 1 Results of logistic regression analysis
指标因子 B S.E Wals df Sig. exp（B） 裸岩信息 0.925 0.456 4.119 1 0.042 2.523 流域面积 0.880 0.394 5.000 1 0.025 2.412 沟床纵比降 1.042 0.186 31.348 1 0 2.834 河流 1.000 0.122 66.763 1 0 2.717 道路 0.879 0.105 69.489 1 0 2.409 断层密度 0.995 0.442 5.059 1 0.024 2.704 土地利用 0.541 0.245 4.888 1 0.027 1.718 土壤类型 0.603 0.112 18.239 1 0 1.828 隐患点密度 0.896 0.297 63.593 1 0 2.449 沟谷密度 1.295 0.211 19.043 1 0 3.650 年降水量 1.064 0.281 25.459 1 0 2.897 常量 −1.485 0.281 27.852 1 0 0.226 注：B为逻辑回归系数；S.E.为标准误差；Wals为卡方值统计量；df为自由度；Sig.为显著性。 
下载: 导出CSV
表 2 泥石流灾害的概率占比
Table 2 Probability proportion of debris flow disaster
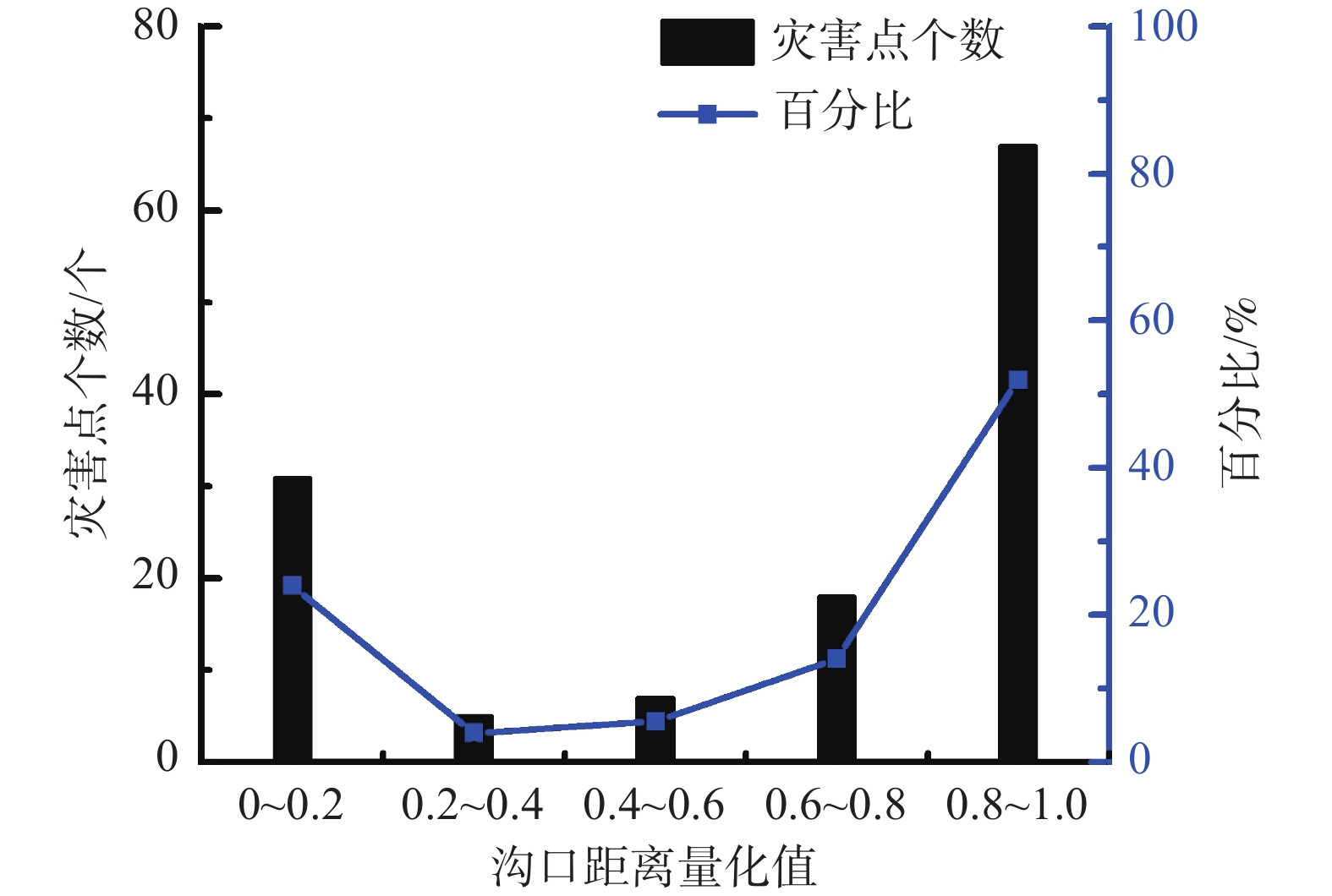
级别 取值区间 灾害点数量 百分比/% 一级 [0, 0.2) 8 6.25 二级 [0.2, 0.4) 5 3.90 三级 [0.4, 0.6) 2 1.56 四级 [0.6, 0.8) 9 7.03 五级 [0.8, 1) 104 81.25
下载: 导出CSV
表 3 径流水深分级
Table 3 Classification of runoff depth
级别 水深区间/m 1 (0, 0.01] 2 (0.01, 0.05] 3 (0.05, 0.1] 4 (0.1, 0.3] 5 >0.3
下载: 导出CSV
表 4 逻辑回归方程表
Table 4 Logistic regression equation table
B S.E. Wald df Sig. exp（B） P 0.790 0.257 9.486 1 0.002 2.204 D 0.834 0.297 7.910 1 0.005 2.303 常量 −5.330 1.432 13.857 1 0.000 0.005 注：B为逻辑回归系数；S.E.为标准误差；Wald为卡方值；df为自由度；Sig.为显著性。
下载: 导出CSV
表 5 泥石流灾害预警验证结果
Table 5 Validation results of debris flow disaster early warning
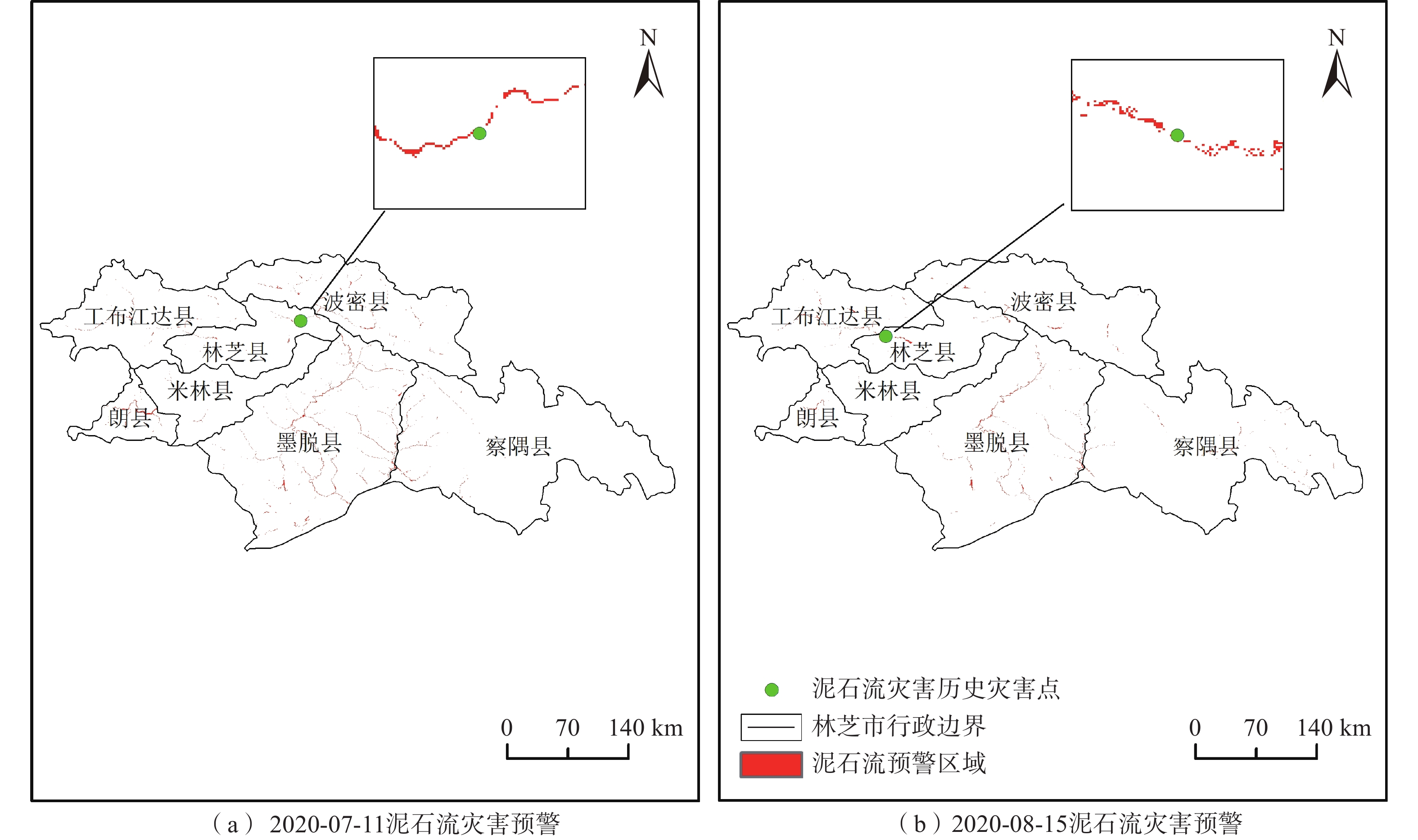
序号 灾害日期 灾害点数/个 预警区内灾害点数/个 1 2011年7月14日 2 1 2 2013年7月6日 1 1 3 2014年4月16日 1 0 4 2014年7月18日 1 0 5 2015年8月6日 5 1 6 2015年8月19日 12 7 7 2015年8月20日 2 2 8 2015年8月21日 3 3 9 2016年4月25日 1 1 10 2016年7月26日 3 3 11 2016年7月27日 2 1 12 2017年8月3日 1 0 13 2017年7月21日 1 1 14 2018年9月9日 1 1 15 2019年7月7日 2 1 16 2020年7月10日 2 2 17 2020年7月11日 3 2 18 2020年8月15日 2 2 合计 45 29
下载: 导出CSV
-
[1] 屈永平, 唐川, 刘洋, 等. 西藏林芝地区冰川降雨型泥石流调查分析[J]. 岩石力学与工程学报, 2015, 34（增刊2）: 4013 − 4022 QU Yongping, TANG Chuan, LIU Yang, et al. Investigation and analysis of glacier debris flow in Nyingchi area, Tibet[J]. Chinese Journal of Rock Mechanics and Engineering, 2015, 34（Sup 2）: 4013 − 4022. （in Chinese with English abstract）
[2] 陈宫燕,普布桑姆,次仁旺姆,等. 基于Logistic回归方法的林芝市山洪地质灾害预警研究[J]. 中国农学通报,2019,35(23):124 − 130. [CHEN Gongyan,PU Busangmu,CI Renwangmu,et al. Early warning of mountain flood geological disasters in Nyingchi based on logistic regression method[J]. Chinese Agricultural Science Bulletin,2019,35(23):124 − 130. (in Chinese with English abstract) DOI: 10.11924/j.issn.1000-6850.casb18040021 [3] 陈宫燕,普布桑姆,次仁,等. 西藏林芝降水引发的山洪地质灾害分布特征[J]. 中国地质灾害与防治学报,2018,29(2):100 − 103. [CHEN Gongyan,PU Busangmu,CIREN,et al. Distribution characteristics of mountain flood and geological disaster caused by precipitation of Nyingchi in Tibet[J]. The Chinese Journal of Geological Hazard and Control,2018,29(2):100 − 103. (in Chinese with English abstract) [4] SALINAS-JASSO J A,VELASCO-TAPIA F,DE LEÓN I N,et al. Estimation of rainfall thresholds for shallow landslides in the Sierra Madre Oriental,northeastern Mexico[J]. Journal of Mountain Science,2020,17(7):1565 − 1580. DOI: 10.1007/s11629-020-6050-2
[5] YAN Y,ZHANG Y,HU W,et al. A multiobjective evolutionary optimization method based critical rainfall thresholds for debris flows initiation[J]. Journal of Mountain Science,2020,17(8):1860 − 1873. DOI: 10.1007/s11629-019-5812-1
[6] 马煜,李彩侠. 地形因子对四川龙溪河流域泥石流发生的影响[J]. 中国地质灾害与防治学报,2018,29(2):16 − 21. [MA Yu,LI Caixia. Effect of topographic factor on the formation of debris flows in Longxi River Area,Sichuan Province[J]. The Chinese Journal of Geological Hazard and Control,2018,29(2):16 − 21. (in Chinese with English abstract) [7] 熊江,唐川,陈明. 泥石流早期识别与监测预警研究进展探讨[J]. 自然灾害学报,2021,30(1):165 − 173. [XIONG Jiang,TANG Chuan,CHEN Ming. Discussion on the research progress of early identification,monitoring and early warning of debris flow[J]. Journal of Natural Disasters,2021,30(1):165 − 173. (in Chinese with English abstract) [8] 王英杰. 岷江上游泥石流预警报模型构建及其应用[D]. 绵阳: 西南科技大学, 2020 WANG Yingjie. Construction and application of debris flow early-warning and forecast model in the upper Min River[D]. Mianyang: Southwest University of Science and Technology, 2020. （in Chinese with English abstract）
[9] PONZIANI M,POGLIOTTI P,STEVENIN H,et al. Debris-flow Indicator for an early warning system in the Aosta valley region[J]. Natural Hazards,2020,104(2):1819 − 1839. DOI: 10.1007/s11069-020-04249-5
[10] 黄健,胡卸文,金涛,等. 四川西昌“3·30”火烧区响水沟火后泥石流成灾机理[J]. 中国地质灾害与防治学报,2022,33(3):15 − 22. [HUANG Jian,HU Xiewen,JIN Tao,et al. Mechanism of the post-fire debris flow of the Xiangshui gully in “3·30” fire area of Xichang, Sichuan Province[J]. The Chinese Journal of Geological Hazard and Control,2022,33(3):15 − 22. (in Chinese with English abstract) [11] 包红军,王凯,张少杰,等. 耦合分布式水文模型的泥石流物理模型预报试验[J]. 暴雨灾害,2018,37(4):303 − 310. [BAO Hongjun,WANG Kai,ZHANG Shaojie,et al. Debris flow forecasting test based on a physical model coupling with a distributed hydrological model[J]. Torrential Rain and Disasters,2018,37(4):303 − 310. (in Chinese with English abstract) [12] 王治华,郭兆成,杜明亮,等. 基于数字滑坡技术的暴雨滑坡、泥石流预警、监测模型研究[J]. 地学前缘,2011,18(5):303 − 309. [WANG Zhihua,GUO Zhaocheng,DU Mingliang,et al. Model study of monitoring and early warning of rainstorm induced landslide and debris flow based on digital landslide technology[J]. Earth Science Frontiers,2011,18(5):303 − 309. (in Chinese with English abstract) [13] 王海芝. 北京地区暴雨泥石流预警阈值研究[J]. 第四纪研究,2020,40(5):1371 − 1380. [WANG Haizhi. Early warning thresholds of the rainfall-induced debris flows in Beijing[J]. Quaternary Sciences,2020,40(5):1371 − 1380. (in Chinese with English abstract) DOI: 10.11928/j.issn.1001-7410.2020.05.24 [14] BUGAETS A N,GARTSMAN B I,TERESHKINA A A,et al. Using the SWAT model for studying the hydrological regime of a small river basin (the komarovka river,primorsky Krai)[J]. Russian Meteorology and Hydrology,2018,43(5):323 − 331. DOI: 10.3103/S1068373918050060
[15] THOMPSON J R,SØRENSON H R,GAVIN H,et al. Application of the coupled MIKE SHE/MIKE 11 modelling system to a lowland wet grassland in southeast England[J]. Journal of Hydrology,2004,293(1/2/3/4):151 − 179.
[16] 王济,蔡雄飞,雷丽,等. 不同裸岩率下我国西南喀斯特山区土壤侵蚀的室内模拟[J]. 中国岩溶,2010,29(1):1 − 5. [WANG Ji,CAI Xiongfei,LEI Li,et al. Laboratory simulation on soil erosion under different bedrock outcrop rate in Southwest Karst area, China[J]. Carsologica Sinica,2010,29(1):1 − 5. (in Chinese with English abstract) [17] LIU W, HE S. Comprehensive modelling of runoff-generated debris flow from formation to propagation in a catchment. Landslides, 2020, 17（4）: 1529 − 1544.
[18] 张书豪,吴光,张乔,等. 基于子流域特征的泥石流易发性评价[J]. 水文地质工程地质,2018,45(2):142 − 149. [ZHANG Shuhao,WU Guang,ZHANG Qiao,et al. Debris-flow susceptibility assessment using the characteristic factors of a catchment[J]. Hydrogeology & Engineering Geology,2018,45(2):142 − 149. (in Chinese with English abstract) [19] 张以晨,秦胜伍,翟健健,等. 基于信息量的长白山地区泥石流易发性评价[J]. 水文地质工程地质,2018,45(2):150 − 158. [ZHANG Yichen,QIN Shengwu,ZHAI Jianjian,et al. Susceptibility assessment of debris flow based on GIS and weight information for the Changbai Mountain area[J]. Hydrogeology & Engineering Geology,2018,45(2):150 − 158. (in Chinese with English abstract) [20] 张盼盼,胡远满,肖笃宁,等. 一种基于多光谱遥感影像的喀斯特地区裸岩率的计算方法初探[J]. 遥感技术与应用,2010,25(4):510 − 514. [ZHANG Panpan,HU Yuanman,XIAO Duning,et al. A method of the percentage of bare rock calculation in Karst areas based on multi-spectrum remote sensing image[J]. Remote Sensing Technology and Application,2010,25(4):510 − 514. (in Chinese with English abstract) DOI: 10.11873/j.issn.1004-0323.2010.4.510 [21] 陈冠,孟兴民,郭鹏,等. 白龙江流域基于GIS与信息量模型的滑坡危险性等级区划[J]. 兰州大学学报(自然科学版),2011,47(6):1 − 6. [CHEN Guan,MENG Xingmin,GUO Peng,et al. Landslide susceptibility mapping based on GIS and information value model in Bailong River Basin[J]. Journal of Lanzhou University (Natural Sciences),2011,47(6):1 − 6. (in Chinese with English abstract) [22] 王卫东,钟晟. 基于GIS的Logistic回归模型在地质灾害危险性区划中的应用[J]. 工程勘察,2009,37(11):5 − 10. [WANG Weidong,ZHONG Sheng. The application of GIS-based logistic regression for geological hazards zonation[J]. Geotechnical Investigation & Surveying,2009,37(11):5 − 10. (in Chinese with English abstract) [23] HOCK R. Glacier melt:A review of processes and their modelling[J]. Progress in Physical Geography:Earth and Environment,2005,29(3):362 − 391. DOI: 10.1191/0309133305pp453ra
[24] 张勇,刘时银. 度日模型在冰川与积雪研究中的应用进展[J]. 冰川冻土,2006,28(1):101 − 107. [ZHANG Yong,LIU Shiyin. Progress of the application of degree-day model to study glaciers and snow cover[J]. Journal of Glaciology and Geocryology,2006,28(1):101 − 107. (in Chinese with English abstract) DOI: 10.3969/j.issn.1000-0240.2006.01.014 [25] 闫玉娜,车涛,李弘毅,等. 使用积雪遥感面积数据改善山区春季融雪径流模拟精度[J]. 冰川冻土,2016,38(1):211 − 221. [YAN Yuna,CHE Tao,LI Hongyi,et al. Using snow remote sensing data to improve the simulation accuracy of spring snowmelt runoff:Take Babao River Basin as an example[J]. Journal of Glaciology and Geocryology,2016,38(1):211 − 221. (in Chinese with English abstract) [26] OMANI N,SRINIVASAN R,SMITH P K,et al. Glacier mass balance simulation using SWAT distributed snow algorithm[J]. Hydrological Sciences Journal,2017,62(4):546 − 560. DOI: 10.1080/02626667.2016.1162907
-
期刊类型引用(23)
1. 马明明，伍尚前，谢猛，童鹏，袁晓波. 决策树分类在铁路沿线桉树提取及滑坡隐患识别中的应用——以贵广高铁广西段为例. 中国地质灾害与防治学报. 2025(01): 37-45 . 
本站查看
2. 刘亚静，刘红健. 基于信息量-随机森林模型的地震带地质灾害易发性评价：以松潘-较场地震带为例. 科学技术与工程. 2024(01): 143-154 . 百度学术
3. 黄海，江思义，李海良，李春玲，吴秋菊. 岩溶地区危岩和岩质崩塌易发性评价研究——以广西贺州市平桂区为例. 成都理工大学学报(自然科学版). 2024(01): 137-151 . 百度学术
4. 刘玥，申玉松，李旭，张迪. 基于不同耦合模型的区域地质灾害易发性评价——以河南商城县为例. 中国地质调查. 2024(01): 83-92 . 百度学术
5. 高茂宁，魏冠军，雷传金，张沛. 顾及时序InSAR的海东市辖区滑坡敏感性评价. 地理空间信息. 2024(05): 97-101 . 百度学术
6. 石文君，王宇栋，解晋航，李章杰，梁形形. 基于多种模型对比的寻甸县地质灾害易发性分析. 矿产勘查. 2024(06): 1092-1102 . 百度学术
7. 寸得欣，令狐昌卫，马一奇，尹林虎，陈庆松，刘振南，涂春霖. 基于GIS和加权信息量模型的富源县地质灾害易发性评价. 科学技术与工程. 2024(18): 7563-7573 . 百度学术
8. 冯振，陈亮，王立朝，侯圣山，田怡帆，刘明学. 区域地质灾害易发性评价的证据权法原理与实践. 地质通报. 2024(07): 1255-1265 . 百度学术
9. 张宇，简季，郝利娜，杨鑫. 基于IV-MLP耦合模型的龙陵县滑坡易发性评价. 物探化探计算技术. 2024(05): 618-626 . 百度学术
10. 桂富羽，史正涛，喜文飞，付尧，郭峻杞. 基于证据权模型的滑坡灾害易发性评价研究——以普洱市为例. 城市勘测. 2024(05): 188-193+198 . 百度学术
11. 梁峰，江攀和. 基于IVM-CF耦合模型的贵定县滑坡地质灾害易发性评价. 水利水电技术(中英文). 2024(S2): 669-677 . 百度学术
12. 裴鹏程，黄帅，袁静，张智康. 走滑断层作用下上覆土层的变形破坏机理. 中国地质灾害与防治学报. 2024(06): 115-127 . 本站查看
13. 赖波，赵风顺，江金进，江山，江宁，李俊生. 基于AHP-信息量法的珠海市地质灾害风险评价. 华南地质. 2023(01): 147-156 . 百度学术
14. 阮征，周少伟，姚胜，田垚. 黄土高原腹地地质灾害致灾因素分析及易发性评价. 科技导报. 2023(10): 115-124 . 百度学术
15. 王伟中，李树兴，杨成，许涛，宋飞，曹小红，李浩然，王伟华. 基于GIS和证据权模型的山阳县地质灾害易发性评价. 新疆地质. 2023(02): 262-269 . 百度学术
16. 黄鑫，吴珍云，丁德建，李希星，石祖峰，祝民强，孙彬涵. 基于信息量-逻辑回归模型的江西省婺源县地质灾害易发性评价. 东华理工大学学报(自然科学版). 2023(03): 259-268 . 百度学术
17. 曾斌，吕权儒，寇磊，艾东，许汇源，袁晶晶. 基于Logistic回归和随机森林的清江流域长阳库岸段堆积层滑坡易发性评价. 中国地质灾害与防治学报. 2023(04): 105-113 . 本站查看
18. 胡杨，张紫昭，林世河. 基于证据权与逻辑回归耦合的新疆伊犁河谷地区滑坡易发性评价. 工程地质学报. 2023(04): 1350-1363 . 百度学术
19. 张潇远，苏巧梅，赵财胜，朱月琴，李凯新，范锦龙，白东升. 一种利用贝叶斯算法优化XGBoost的滑坡易发性评价方法. 测绘科学. 2023(06): 140-150 . 百度学术
20. 张华湘，孙乾征，樊善兴，杨子林. 滑坡易发性评价方法和精度比较——以贵州省大方县为例. 贵州地质. 2023(03): 302-309+295 . 百度学术
21. 龚芯磊，张斌，高金利，杨洪森. 基于斜坡单元尺度AHP-信息量模型的重点区域地质灾害风险评价——以贵州省紫云县中部重点区为例. 贵州地质. 2023(03): 310-320 . 百度学术
22. 谭燕，崔雨，金华丽，方龙建，葛鹏，付乐意. 基于信息量模型及层次分析法的镇江丹徒区滑坡崩塌地质灾害易发性评价. 昆明冶金高等专科学校学报. 2023(04): 7-15 . 百度学术
23. 董凯，王永卿，蒲秀勇，梁凯丽. 基于信息量法的广西南宁市武鸣区地质灾害易发性评价. 农业灾害研究. 2023(09): 300-303 . 百度学术
其他类型引用(8)
计量
- 文章访问数: 1974
- HTML全文浏览量: 1667
- PDF下载量: 239
- 被引次数: 31
邮件订阅
RSS