Deformation mechanism and optimum supporting structures in fault-bearing biased tunnels
-
摘要:
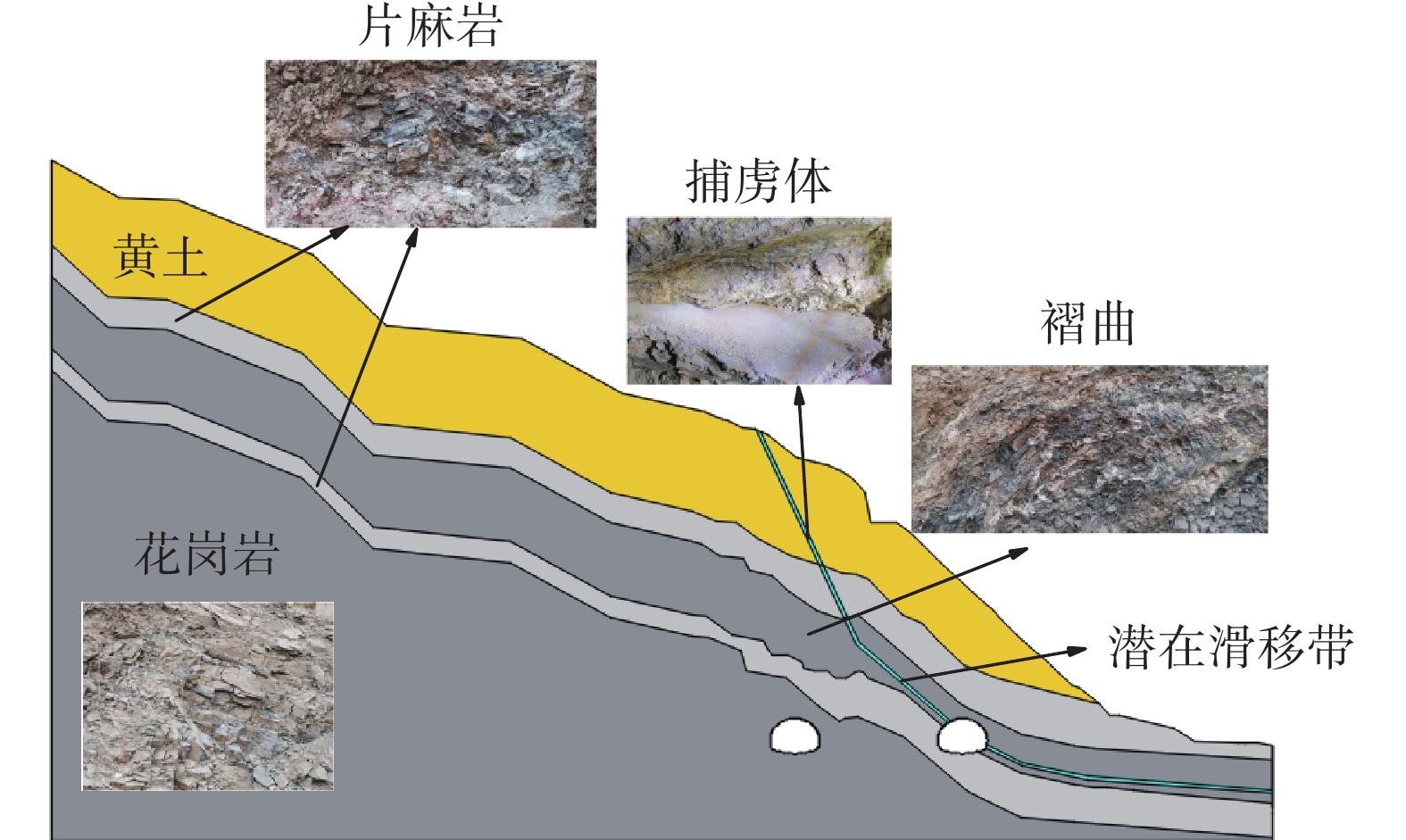
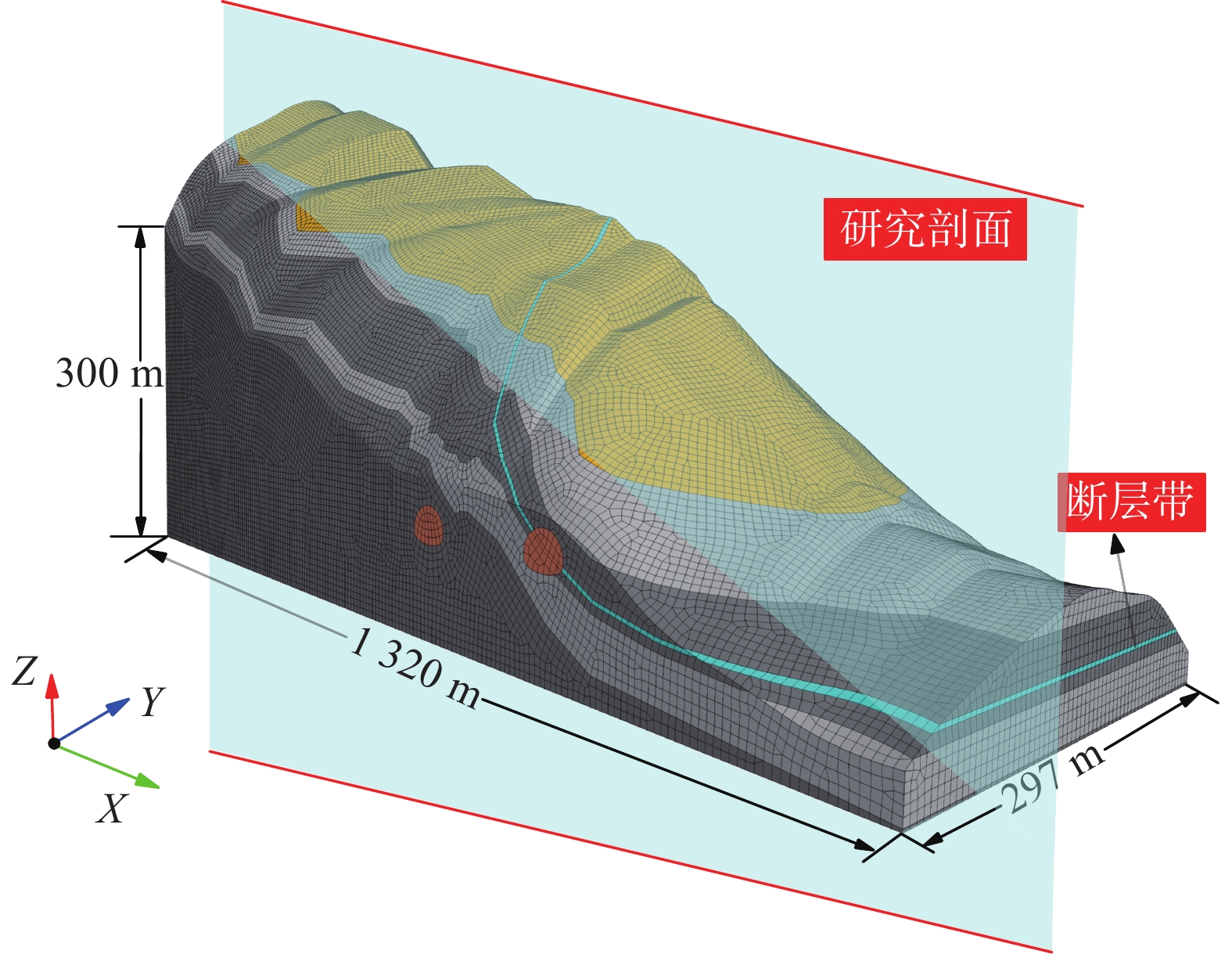
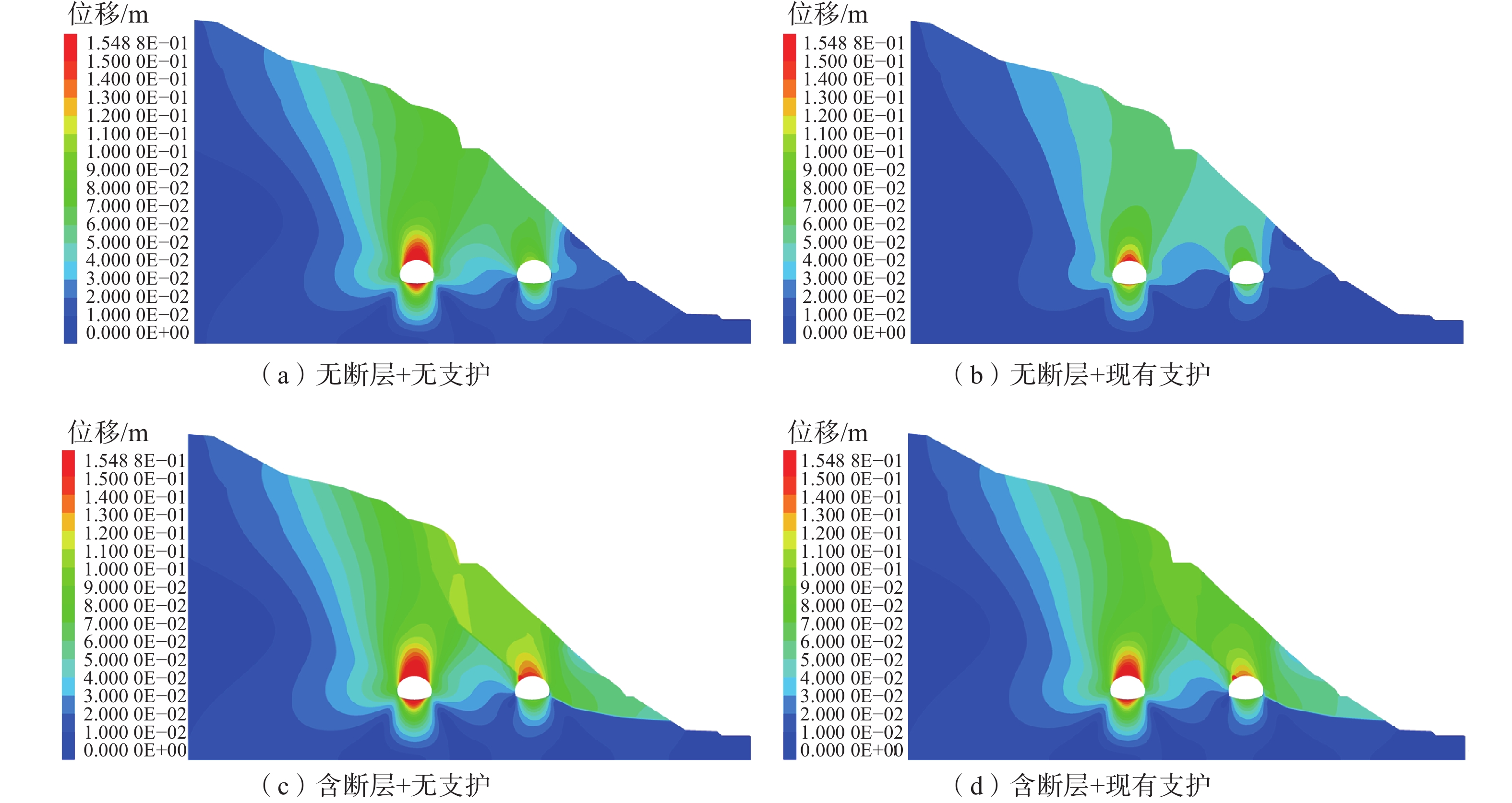
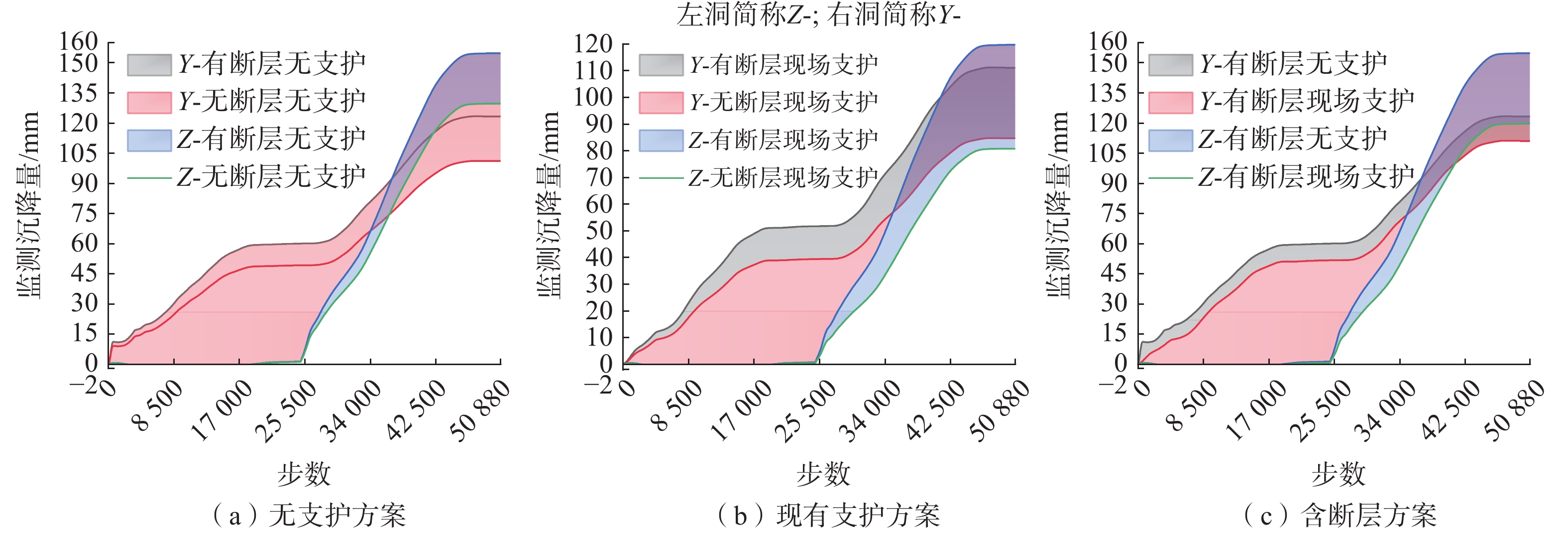
为探明复杂地质条件下隧道围岩变形机理，制定相适应的围岩变形控制技术，以清泉隧道为工程依托，对偏压隧道洞口段围岩变形进行分析，基于FLAC3D研究有无断层条件下不同支护状态围岩稳定性，明确围岩变形机理并提出控制措施。研究表明：（1）偏压效应下后行洞开挖扰动使上覆围岩与断层带相交层面张开、层间岩体弯折破裂，围岩应力重分布且断层破碎带进一步恶化，导致围岩变形严重；（2）软弱围岩自稳能力差，二次应力作用使得小净距隧道顶拱、边墙围岩产生可持续塑性变形，伴随着时间效应，对支护结构逐渐产生挤压变形，现有支护方案不能提供足够的支护强度和刚度以抵抗围岩变形；（3）提出的坡面锚索+深埋侧抗滑桩复合控制措施，可有效控制围岩变形，减弱断层破碎带恶化对围岩稳定性影响，数值计算结果与现场监测结果较为吻合。研究结果可为类似复杂地质条件下隧道围岩变形控制提供参考。
Abstract:To explore the deformation mechanisms of tunnel surrounding rock under complex geological conditions and develop appropriate technologies for controlling surrounding rock deformation, this study analyzes the deformation of surrounding rock at the mouth section of a biased tunnel, using the Qingquan Tunnel as a case study. Based on FLAC3D, stability of surrounding rock under different support conditions with and without faults is studied to clarify the deformation mechanism of the surrounding rock and propose effective control measures. The study shows that: (1) Excavation disturbances during backward hole excavation under biased conditions cause tensional interaction between the overlying surrounding rock and fault zones, leading to the interlayer rock body bending, rupturing, and stress redistribution, exacerbating the fragmentation of fault zones and resulting in significant surrounding rock deformation. (2) Weak surrounding rock exhibits limited self-stabilization capacity; secondary stress induces sustainable plastic deformation in small clear span tunnel roofs and sidewalls, gradually causing squeezing deformation in support structures over time. Existing support schemes fail to provide sufficient strength and stiffness to resist surrounding rock deformation. (3) Proposed composite control measures of slope surface anchors and deep-buried lateral anti-sliping piles effectively control surrounding rock deformation, mitigate the adverse impact of fractured fault zones on rock stability, and numerical calculation results align closely with on-site monitoring results. The findings provide valuable insights for deformation control of tunnel surrounding rock under similar complex geological conditions.
-
0. 引言
地基稳定性受多种因素影响[1 − 2]，特别是黄土地区，受震陷影响很大。黄土震陷作为一种严重的地质灾害，一旦发生将会造成非常严重的后果。前人对与黄土震陷的研究基本是以动三轴试验为主，以单个震陷量作为震陷性的主要的评价指标[3 − 6]。然而黄土地基震陷的准确性评价受到土性参数不确定性的影响，其中物理力学指标的概率分布类型和变异性会对评价结果产生影响。针对岩土工程中参数、计算模型、荷载等不确定性问题，其主要的不确定性分析方法包括：概率分析方法[7]、随机有限元法[8]、灰色系统评价法[9]、模糊数学法[10]、神经网络评价方法[11]等。这些不确定性方法可以考虑得更加全面，从而提高评价结果的准确性，使结果更为科学合理。
关于黄土震陷在不确定性方面的研究，李波等[12]采用灰色关联方法和逐步判别方法建立了耦合式软土震陷判别模型从而实现软土震陷等级的判定。在黄土震陷概率评价方面，谭芳[13]将概率地震危险性分析方法引入震陷计算中，采用不确定性分析方法分析了黄土震陷与地震参数之间的关系，从而提出一种考虑地震随机性的黄土震陷预测方法。任森等[14]基于大量动三轴试验，结合场地地震危险性概率分析方法，确定了研究区内的震陷区划。孙军杰等[15]依据残余应变估算模型采用概率统计等非确定性分析方法对地基动力沉降进行了概率分析。可见概率分析方法在土体动力沉降中已经得到了初步研究。
然而到目前为止，还没有研究将可靠度理论应用于黄土地基震陷的分析中。因此本文尝试将可靠度理论应用于黄土地基震陷评价中，使用可靠度方法对黄土地基震陷性进行分析。可靠度方法和传统的确定性分析方法相互补充与结合，有助于进行震陷可靠度分析。
1. 黄土地基震陷可靠度指标
可靠度理论在边坡稳定分析中被广泛应用，而边坡工程的不确定因素主要为土体参数的抗剪强度（内摩擦角、黏聚力）[16 − 18]。其依托蒙特卡洛分析法通过计算出多组安全系数值将小于1的安全系数的次数与计算次数的比值称作失效概率。因此可求得对应的可靠度指标（$ \mathrm{\beta } $）为：
$$ \beta ={\varPhi }^{-1}(1-{P}_{\text{f}}) $$ (1) 式中：$ \varPhi $——标准正态分布的累计分布函数；
${P_{\text{f}}}$——失效概率。
在目前已有的地震灾害评估中，尚未有关于地基震陷量的标准划分依据。根据中国地震局发布的《震害调查及地震损失评定工作指南》，可以采用“地基基础破坏等级标准”来评估震陷灾害的程度[16]，将震陷量小于2 cm的定义为基本完好，震陷量大于40 cm的定义为破坏。
参考可靠度理论在边坡稳定性评价中的应用，结合黄土动力学对震陷等级的划分，本文提出了一种对黄土地基震陷评价的可靠度指标。
（1）最大可靠度
在震陷等级划分中将震陷量大于40 cm的定义为震陷破坏，因此可采用破坏概率（Pd）来判定其震陷破坏状态，即$ {P_{\mathrm{d}}} = P\left( {S \geqslant 40} \right) $。将$ \beta_{\mathrm{d}} $定义为：
$$ {\beta _{\mathrm{d}}} = \frac{{40 - {u_{\mathrm{s}}}}}{{{\sigma _{\mathrm{s}}}}} $$ (2) 式中：$ {u_{\mathrm{s}}} $——震陷量的平均值；
$ {\sigma _{\mathrm{s}}} $——震陷量的标准差。
如果震陷量符合标准正态分布，破坏概率与可靠度的关系可表示为：
$$ {P_{\mathrm{d}}} = P\left( {S > 40} \right) = 1 - \varPhi \left(\frac{{40 - {u_{\mathrm{s}}}}}{{{\sigma _{\mathrm{s}}}}}\right) = 1 - \varPhi ({\beta _{\mathrm{d}}}) $$ (3) 则根据可靠度理论，将破坏概率对应的可靠度称为最大可靠度（${\beta }_{\text{d}} $），也就是指衡量地基震陷最大安全程度的标准，其计算公式为：
$$ {\beta }_{\text{d}}={\varPhi }^{-1}(1-{P}_{\text{d}}) $$ (4) 根据蒙特卡罗可靠度计算方法可定义破坏概率为：
$$ {P_{\text{d}}} = \frac{M}{N} $$ (5) 式中：$ {P}_{{\mathrm{d}}} $——地基震陷破坏概率；
M——抽样次数中震陷量大于40 cm的次数；
N——蒙特卡洛分析法总的抽样次数。
（2）最小可靠度
在震陷等级划分中将震陷量小于2 cm的定义为基本完好，因此可采用完好概率（Ph）来判定其完好状态，即$ {P_{\mathrm{h}}} = P\left( {S \leqslant 2} \right) $。将$ {\beta _{\mathrm{h}}} $定义为：
$$ {\beta _{\mathrm{h}}} = \frac{{2 - {u_{\mathrm{s}}}}}{{{\sigma _{\mathrm{s}}}}} $$ (6) 式中：$ {u_{\mathrm{s}}} $——震陷量的平均值；
$ {\sigma _{\mathrm{s}}} $——震陷量的标准差。
如果震陷量符合标准正态分布，完好概率（Ph）与可靠度的关系可表示为：
$$ {P_{\mathrm{h}}} = P\left( {S < 2} \right) = \varPhi \left(\frac{{2 - {u_{\mathrm{s}}}}}{{{\sigma _{\mathrm{s}}}}}\right) = \varPhi ({\beta _{\mathrm{h}}}) $$ (7) 根据可靠度理论，将完好概率对应的可靠度称为最小可靠度（${\beta _{\mathrm{h}}} $），也就是指衡量地基震陷完好程度的标准，其计算公式为：
$$ {\beta _{\text{h}}} = {\varPhi ^{ - 1}}\left( {{P_{\text{h}}}} \right) $$ (8) 根据蒙特卡罗可靠度计算方法可定义完好概率为：
$$ {P_{\text{h}}} = \frac{M}{N} $$ (9) 式中：$ {P}_{{\mathrm{h}}} $——地基完好概率；
M——抽样次数中震陷量小于2 cm的次数；
N——蒙特卡洛分析法总的抽样次数。
2. 基于Kriging代理模型的震陷可靠度计算
2.1 Kriging代理模型的建立
Kriging模型是一种基于方差最小的无偏估计方法，它的原理是通过已知样本点的线性加权法来预测未知点的函数值，即已知加权系数插值就可求得变量空间内任一点的函数值。Kriging代理模型通常情况下由回归部分和随机误差两部分所组成。将其用输出变量S(x)与输入变量x表示为：
$$ S({\boldsymbol{x}}) = \sum\limits_{i = 1}^m {{\beta _i}} f({\boldsymbol{x}}) + {\textit{z}}({\boldsymbol{x}}) = f{({\boldsymbol{x}})^T}{\boldsymbol{\beta}} + {\textit{z}}({\boldsymbol{x}}) $$ (10) 式中：每个样本点中输入变量的个数为n，$ {\boldsymbol{x}} = [ {x_1},{x_2}, \cdots , {x_n} ]^T$，$ f(x) = {\left[ {{f_1}(x),{f_2}(x), \cdots ,{f_m}(x)} \right]^T} $为回归多项式基函数向量，m为回归多项式的数量；${\boldsymbol{\beta}} = {[{\beta _1},{\beta _2},\cdots,{\beta _m}]^T}$为多项式参数向量，z(x)为一均值为0，方差为$ {\sigma ^2} $的正态随机过程，该随机过程的协方差为：
$$ COV\left[{\textit{z}}(u),{\textit{z}}(v)\right]={\sigma }^{2}R({u,v}) $$ (11) 其中，R表示任意两点u，v的相关函数，通常取为高斯相关方程，即：
$$ R(u,v) = \exp \left\{ { - \theta {{(u - v)}^2}} \right\} $$ (12) 其中，$ \theta $为相关参数，可通过最大似然估计得到：
$$ \theta=\max \left\{ { - \left[ {\frac{1}{2}\ln \left( {\left| R \right|} \right)} \right] + \frac{k}{2}\ln \left( {{\sigma ^2}} \right)} \right\} $$ (13) 其中，R为相关矩阵，元素R=R(u,v)。
基于给定的样本点，多项式参数向量$\beta $与随机过程方差$ {\sigma ^2} $的估计值分别为：
$$ \left\{ {\begin{split} & {\hat {\boldsymbol{\beta}} = {{\left( {{{\boldsymbol{F}}^T}{{\boldsymbol{R}}^{ - 1}}{\boldsymbol{F}}} \right)}^{ - 1}}{{\boldsymbol{F}}^T}{{\boldsymbol{R}}^{ - 1}}{\boldsymbol{Y}}} \\ & {{{\hat {\boldsymbol{\sigma}} }^2} = \frac{1}{k}{{\left( {{\boldsymbol{Y}} - {\boldsymbol{F}}\hat {\boldsymbol{\beta}} } \right)}^T}{{\boldsymbol{R}}^{ - 1}}\left( {{\boldsymbol{Y}} -{\boldsymbol{ F}}\hat {\boldsymbol{\beta}} } \right)} \end{split}} \right. $$ (14) 其中，F为由回归多项式函数值构成的矩阵。
对于任意输入变量$ {x_0} $,假定$ {x_0} $与输入变量样本X之间的相关系数向量为$ {{\boldsymbol{r}}_0} = {\left[ {R\left( {{x_0},{x_1}} \right), \cdots ,R\left( {{x_0},{x_k}} \right)} \right]^T} $利用式（10）构建的Kriging模型表达式，可以得到与$ {x_0} $对应的系统响应值$ S({x_0}) $的预测值$ \hat S({x_0}) $服从正态分布$ N(\hat S({x_0}),{\hat \sigma _{\hat S}}^2({x_0})) $,$ S({x_0}) $的最佳线性无偏估计及均方误差可表示为：
$$ \left\{ {\begin{split} &{\hat S\left( {{x_0}} \right) = {f^T}({x_0})\hat {\boldsymbol{\beta}} + {{\boldsymbol{r}}_0}^T{{\boldsymbol{R}}^{ - 1}}({\boldsymbol{Y}} - {\boldsymbol{F}}\hat {\boldsymbol{\beta }})} \\ & {{{\hat \sigma }^2}_{\hat S}({x_0}) = {{\hat \sigma }^2}\left( {1 + {{\boldsymbol{u}}^T}{{({{\boldsymbol{F}}^T}{{\boldsymbol{R}}^{ - 1}}{\boldsymbol{F}})}^{ - 1}}{\boldsymbol{u}} - {{\boldsymbol{r}}_0}^T{{\boldsymbol{R}}^{ - 1}}{{\boldsymbol{r}}_0}} \right)} \end{split}} \right. $$ (15) 其中，$ {{{\boldsymbol{u}} = }}{{{{\boldsymbol{F}}}}^T}{{\boldsymbol{R}}^{ - 1}}{{\boldsymbol{r}}_0} - {\boldsymbol{f}} $。
本文进行震陷可靠度分析时，式（10）—（15）中应用Kriging模型构建和预测其过程，采用MATLAB中的DACE工具箱实现。
2.2 黄土地基数值模型
采用FLAC3D有限差分软件建立黄土地基数值模型，模型尺寸设置为15 m×15 m×15 m，模型网格数为
3375 ，本构模型选择Mohr-Coulomb弹塑性本构模型。在静力分析时，底面和侧面选用固定边界，限制底面与侧面的位移和速度，顶部为自由边界。动力分析与静力分析不同，由于地震荷载会存在波的反射，因此在模型底面设置静态边界，侧面设置为自由场边界，模拟土体在实际中的状态（图1）。本文选用三条地震波分别是Kobe地震波、Imperial地震波和一条人工合成波。为方便后续说明，这里将选用的三条地震波分别命名为地震波1、地震波2及地震波3。地震波1的持续时间为25 s，时间间隔为0.02 s，最大加速度为0.345g，地震波2的持续时间为40 s，时间间隔为0.01 s，最大加速度为0.313g，地震波3的持续时间为20 s，时间间隔为0.02 s，最大加速度为0.153g。图2为经过滤波以及基线校正后所选地震波的时程曲线。
为了研究不同地震水平作用下震陷变形规律，将其改变幅值的大小来满足不同工况的需要，得到 0.1g、0.2g、0.3g、0.4g、0.5g、0.6g、0.7g不同峰值加速度大小的7种水平。其计算所得震陷量结果如表1所示。
表 1 不同地震波及不同峰值加速度作用下地基震陷量Table 1. Seismic subsidence of foundation under different seismic waves and peak accelerations.峰值加速度/g 震陷量/cm 地震波1 地震波2 地震波3 0.1 0.72 1.95 2.65 0.2 2.37 8.40 13.44 0.3 9.10 16.02 21.62 0.4 17.83 21.44 29.52 0.5 19.78 25.29 37.06 0.6 20.08 30.67 40.98 0.7 20.48 35.84 46.98 2.3 震陷变形影响因素敏感性分析
岩土体材料参数存在着变异性，但土体泊松比的变异系数非常小，在考虑土性参数不确定时可将其看作常量。孙军杰等[17]通过理论分析，给出了非饱和黄土动残余应变与黏聚力、内摩擦角、初始孔隙比、土层重度、土层埋深以及地震动荷载之间的定量关系式。压缩模量是体现土体压缩性的指标之一，作为土体的力学性质，在分析地基土体变形或沉降时起着重要作用，而土体的黏聚力和内摩擦角反映土体的强度特征，在静力分析中，黄土地基静力参数中密度对于计算结果的影响较明显。因此，这里选择密度、弹性模量、黏聚力及内摩擦角四种参数。采用FLAC3D结合灰色关联分析对影响黄土地基震陷变形的因素做敏感性分析，求得其密度、弹性模量、黏聚力及摩擦角四个参数的灰色关联度为$ q = [ {0.656\;8},\;{0.856\;2},\;{0.668\;5},\;{0.728\;1} ] $，敏感性排序为：弹性模量>内摩擦角>黏聚力>密度。
2.4 土性参数分布概率模型
本节选取密度（ρ）、压缩模量（Es）、黏聚力（c）及内摩擦角（φ）四种参数作为黄土震陷性评价的参数指标来进行分布概率模型研究。为了全面分析不同地貌单元4种土性参数的最优概率分布，选用可以包含大部分不确定性因素的概率分布形式包括正态分布、对数正态分布和威布尔分布进行假设检验。从而确定每个参数的最优概率分布形式[18]。
为获取原状黄土地基土性不同参数的分布概率模型，基于引汉济渭工程的渭河二级阶地地貌土体为例，通过对原状黄土的各种物理力学指标进行统计分析，得出各指标服从的概率密度函数及分布参数，图3所示为渭河二级阶地分布概率模型图，其中$ f\left( x \right) $表示概率密度函数。
![]()
图 3 不同参数的概率密度分布图Figure 3. Probability density distribution plots of different parameters由图3可知，从分布形态上来看，$ \rho $值的正态分布和对数正态分布整体较一致，两者均属于左偏态；其余三种土性参数正态分布、对数正态分布及威布尔分布三者分布较离散，差异性较大。
通过K-S检验法对4种土性参数的3种分布概率模型进行检验，求出样本值的理论累计概率分布与经验累计概率分布的最大差值（Dmax），与由显著性水平和样本数确定临界值（$ D_n^\alpha $）进行比较，计算结果如表2所示。四种参数均可接受正态分布、对数正态分布和威布尔分布。$ c $、$ {E_{\mathrm{s}}} $值的最优分布是正态分布，$ \varphi $、$ \rho $值的最优分布是威布尔分布，考虑到正态分布的优良性质，将正态分布作为4种土性参数的分布概率模型用于震陷可靠度计算。
表 2 分布假设检验结果Table 2. Distribution hypothesis test results检验参数 样本量 验证结果$ {D_{\max }} $ 可接受的临界值
$ D_n^\alpha /\left( {\alpha = 0.05} \right) $正态分布 对数正态分布 威布尔分布 结果 $ {D_{\max }} $ 结果 $ {D_{\max }} $ 结果 $ {D_{\max }} $ 内摩擦角 24 √ 0.180 √ 0.223 √ 0.093 0.273 黏聚力 24 √ 0.099 √ 0.125 √ 0.102 0.273 压缩模量 24 √ 0.094 √ 0.146 √ 0.164 0.273 密度 48 √ 0.150 √ 0.185 √ 0.115 0.196 2.5 基于Kriging代理模型的震陷可靠度计算方法
本节基于Kriging代理模型对地基震陷可靠度进行计算，这里进行
10000 次模拟，计算步骤如下：（1）根据前文统计出的土性参数（密度、压缩模量、黏聚力、摩擦角）的概率分布模型，确定地基土体参数的均值、标准差、分布类型等统计特性。
（2）FLAC3D6.0内置有Python编程语言，可以实现蒙特卡洛抽样与连续计算，利用Itasca开发的专门用于Python扩展编程的程序库，通过编程实现随机变量拉丁超立方抽样（LHS）、模型的建立以及计算，即会产生N组计算方案$ \left(\rho_1,E_{\mathrm{s}1},c_1,\varphi_1\right),\left(\rho_2,E_{\mathrm{s}2},c_2,\varphi_2\right),\cdots,(\rho_n,E_{\mathrm{s}n},c_n, \varphi_n) $，然后计算出对应的响应值。将计算模型文件保存为“n.f3sav”，后续模型按顺序编号，并将其作为源文件以便后续提取。
（3）对地震波设计不同的工况组合，计算每组工况下LHS的样本所对应的震陷量，并保存计算模型。
（4）利用Python编程语言从结果文件中批量提取竖向变形。
（5）采用MATLAB软件分别建立不同工况下的Kriging代理模型，以4种土体参数为输入，相应的地基震陷量为输出，对代理模型进行训练，得到满足精度要求的代理模型。经适当训练的代理模型能够较好地逼近实际情况，在此基础上可以十分方便地预测震陷值从而实现震陷可靠度的计算（图4）。
![]()
图 4 基于Kriging代理模型的震陷可靠度计算流程Figure 4. Calculation process of seismic subsidence reliability based on the Kriging surrogate model3. 算例分析
为验证本文提出方法的适用性，本节以引汉济渭工程为背景结合Kriging代理模型的震陷概率计算方法开展黄土地基震陷可靠度分析。
（1）最大可靠度
表3为不同地震波及不同地震峰值加速度作用下地基震陷的破坏概率，以渭河二级阶地为例。
表 3 不同地震波作用下地基震陷破坏概率Table 3. Probability of foundation subsidence failure under different seismic wave effects加速度/g 地震波1 地震波2 地震波3 0.1 0 0 0 0.2 0 0 0 0.3 0 0 0 0.4 0 0.072 0.116 0.5 0 0.17 0.378 0.6 0 0.232 0.704 0.7 0.002 0.264 0.888 由表3可知，在地震波1的作用下，该地基土体在地震波峰值加速度为0.7g时会出现破坏的概率，在地震波2和地震波3的作用下，在峰值加速度达到0.4g时会出现破坏的概率。三条地震波在峰值加速度达到最大时，其产生的破坏概率也有巨大差异，地震波1在峰值加速度为0.7g时破坏概率为0.002，地震波2在峰值加速度为0.7g时破坏概率为0.264，地震波3在峰值加速度为0.7g时破坏概率为0.888。
依据式（4）求得最大可靠度指标，图5为不同地震波作用下地基震陷的可靠度指标随峰值加速度的变化规律，最大可靠度指标的范围为−1.216～4.526。总体上可靠度指标随峰值加速度的增加呈非线性减小。但三条地震波的减小斜率并不相同，在地震波3作用下，可靠度指标随峰值加速度的变化斜率最大，说明在地震波3作用下，地基的可靠度受地震波峰值加速度的影响最大。对于已知地震波峰值加速度，可以快速粗略估计地基震陷的破坏概率，而不是单纯以震陷量来评价，这在风险评估中具有更为重要的意义。
![]()
图 5 可靠度分析获得的地基震陷最大可靠度Figure 5. Maximum reliability index of foundation seismic subsidence obtained from reliability analysis（2）最小可靠度
表4为不同地震波及不同地震峰值加速度作用下地基震陷的破坏概率，以渭河二级阶地为例。由表4可知，在地震波1的作用下，该地基土体在地震波峰值加速度为0.1g～0.7g时均会出现完好概率，在地震波2和地震波3的作用下，在峰值加速度分别达到0.4g及以后和0.3g及以后完好概率均为0。
表 4 不同地震波作用下地基震陷完好概率Table 4. Probability of intact seismic subsidence of foundation under different seismic wave effects加速度/g 地震波1 地震波2 地震波3 0.1 0.946 0.854 0.842 0.2 0.392 0.094 0.832 0.3 0.238 0.004 0 0.4 0.01 0 0 0.5 0.018 0 0 0.6 0.012 0 0 0.7 0.002 0 0 依据式（8）求得最小可靠度指标，图6为在不同地震波作用下地基震陷的最小可靠度随峰值加速度的变化规律，最小可靠度指标的变化范围为−2.878～1.607。从整体来说，随着地震峰值加速度的增大，地基在地震作用下的最小可靠度指标逐渐降低。当地震峰值加速度为0.1g时，震陷最小可靠度较高，都为正值；当地震峰值加速度为0.2g时，地震最小可靠度显著减小，且超过0.2g以后最小可靠度均为负值。
![]()
图 6 可靠度分析获得的地基震陷的最小可靠度指标Figure 6. Minimum reliability index of foundation seismic subsidence obtained from reliability analysis（3）变异系数对震陷可靠度的影响
为了更好地分析随机变量的变异性大小对震陷可靠度的影响，本文计算了各变量在不同变异系数组合情况下，四种土体参数变异系数随地基震陷可靠度的变化情况，工况组合见表5。
表 5 各参数变异系数工况组合表Table 5. Combination table of variation coefficient for each parameter工况 COV 密度 弹性模量 黏聚力 摩擦角 1-1 0.01 0.3 0.2 0.3 1-2 0.05 1-3 0.1 1-4 0.15 1-5 0.2 2-1 0.05 0.05 0.2 0.3 2-2 0.1 2-3 0.2 2-4 0.3 2-5 0.4 3-1 0.05 0.3 0.05 0.3 3-2 0.1 3-3 0.2 3-4 0.3 3-5 0.4 4-1 0.05 0.3 0.2 0.1 4-2 0.2 4-3 0.3 4-4 0.4 4-5 0.5 计算结果如图7所示。由图可知，随各参数变异系数的增加，震陷最大可靠度逐渐减小，而最小可靠度逐渐增大。当$ COV(\rho) $从0.01增加至0.2，相应的$ {\beta _{\text{d}}} $从3.72减小至3.05，最小可靠度（$ {\beta _{\text{h}}} $）从−1.72增加至−1.55，降幅为21.97%，增幅为10.96%；当$ COV(E_{\mathrm{s}}) $从0.05增加至0.4，相应的$ {\beta _{\text{d}}} $从3.89降至3.29，$ {\beta _{\text{h}}} $从−1.89增加至−1.64，降幅为18.24%，增幅为15.24%；当$ COV(c) $从0.05增加至0.4，$ {\beta _{\text{d}}} $从4.26降至2.89，$ {\beta _{\text{h}}} $从−1.81增加至−1.60，降幅为47.40%，增幅为13.13%；当$ COV(\varphi)$从0.1增加至0.5，$ {\beta _{\text{d}}} $从3.72降至2.74，$ {\beta _{\text{h}}} $从−1.99增加至−1.63，降幅为35.77%，增幅为22.09%。对比数据，在同样的增幅下，最大可靠度的变化幅度比最小可靠度的变化幅度大说明最大可靠度对变异系数更为敏感。计算各个参数最大可靠度起末两点斜率的绝对值，分别为3.526、1.714、3.914和2.45，可看出黏聚力变异系数对震陷最大可靠度影响更为显著。
![]()
图 7 不同参数变异系数对震陷可靠度的影响规律Figure 7. The influence of different parameter coefficient of variations on seismic subsidence reliability4. 结论
（1）Kriging代理模型可以在小样本抽样的情况下得到较好的近似拟合效果，达到精度要求，提高了震陷可靠度的计算效率。
（2）采用震陷可靠度方法来评价地基土体的震陷性，能够合理地考虑土性参数的变异性，更加符合实际情况，具有更好的可靠性和适用性，对于已知地震波峰值加速度，可以快速粗略估计地基震陷的破坏概率，而不是单纯的以震陷量来评价，这在风险评估中具有更为重要的意义。
（3）综合4种土体参数的变异系数对震陷可靠度的影响可以发现，最大可靠度对各个参数的变异系数更为敏感，此外四种土体参数中黏聚力的变异系数对震陷最大可靠度的影响更为显著。
-
![]()
图 9 不同围岩变形支护方案下拱顶沉降量
Figure 9. Settlement amount at the arch crown under different surrounding rock deformation control schemes
![]()
图 11 施加最优控制方案后围岩变形控制效果
Figure 11. Effect of the surrounding rock deformation control after implementing the optimal control scheme
![]()
图 13 现场洞口断面沉降监测曲线
Figure 13. Settlement monitoring curve at the on-site tunnel cave section
表 1 计算模型力学参数
Table 1 Mechanical parameters of the computational model
材料 E/GPa υ $m_{\mathrm{b}}^{\mathrm{p}} $ sp/（10−3） mbr sr/（10−3） η* 黄土 3.02 0.25 0.83 0.4 0.69 0.2 0.012 片麻岩 4.89 0.25 1.17 1.3 0.73 0.3 0.0038 花岗岩 8.66 0.25 1.68 3.9 0.82 0.4 0.002 
下载: 导出CSV
表 2 各控制方案及数值计算模型
Table 2 Various control schemes and numerical calculation models
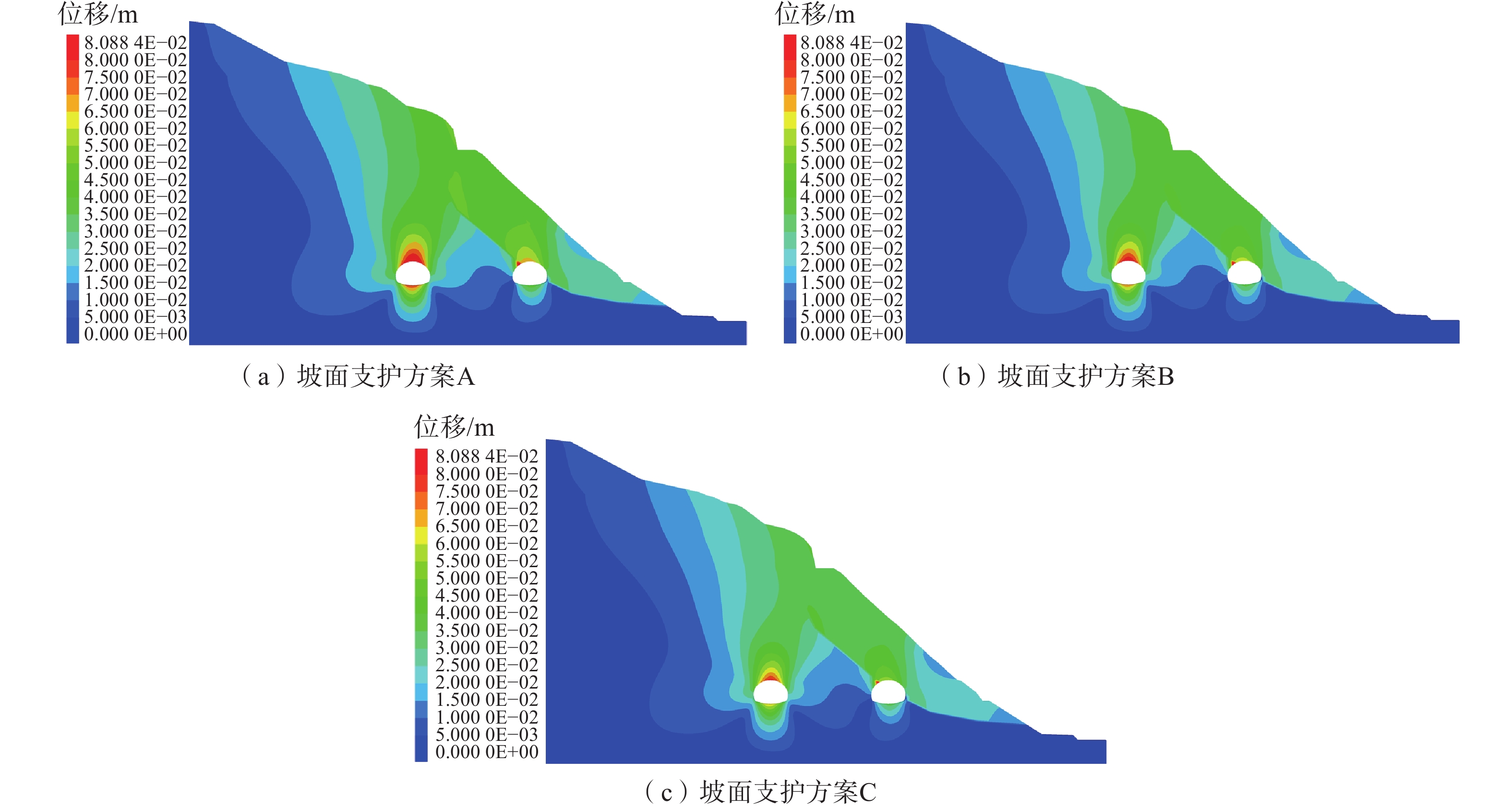
模拟工况 支护参数 支护模型图 支护方案A 现行隧道支护方案+坡面锚索 
支护方案B 现行隧道支护方案+深埋侧抗滑桩（间距8 m） 
支护方案C 现行隧道支护方案+坡面锚索（倾角15°）+深埋侧抗滑桩（间距8 m） 
下载: 导出CSV
表 3 材料参数表
Table 3 Table of material parameters
材料 γ/（kN∙m−3） E/MPa v c/kPa φ/（°） 抗滑桩 25.0 32500 0.2 — — 锚索 22.0 1800 0.35 30 25
下载: 导出CSV
表 4 不同支护参数拱顶沉降量对比表
Table 4 Comparison of vault settlement at the arch crown with different control parameters
支护
参数抗滑桩
桩长/m锚索
倾角/（°）锚固段
长度/m锚索预
应力/kN后行洞拱顶
沉降/mm1 10 15 6 50 68.3 2 15 20 9 100 65.7 3 20 25 12 150 59.4 4 25 30 15 200 53.5 5 30 35 18 250 51.3
下载: 导出CSV
-
[1] 付君宜,陈发达,沈志平,等. 岩溶山区城市地下隧道工程地质灾害风险分析[J]. 中国地质灾害与防治学报,2023,34(3):100 − 108. [FU Junyi,CHEN Fada,SHEN Zhiping,et al. Risk analysis of the geological hazards during urban tunnel construction in mountainous Karst areas[J]. The Chinese Journal of Geological Hazard and Control,2023,34(3):100 − 108. (in Chinese with English abstract)] FU Junyi, CHEN Fada, SHEN Zhiping, et al. Risk analysis of the geological hazards during urban tunnel construction in mountainous Karst areas［J］. The Chinese Journal of Geological Hazard and Control, 2023, 34（3）: 100 − 108. （in Chinese with English abstract）
[2] 昝文博,赖金星,曹校勇,等. 漂卵石隧道围岩力学响应与失稳破坏机制[J]. 岩石力学与工程学报,2021,40(8):1643 − 1653. [ZAN Wenbo,LAI Jinxing,CAO Xiaoyong,et al. Mechanical responses and instability failure mechanisms of surrounding rock of tunnels in boulder-cobble mixed stratum[J]. Chinese Journal of Rock Mechanics and Engineering,2021,40(8):1643 − 1653. (in Chinese with English abstract)] ZAN Wenbo, LAI Jinxing, CAO Xiaoyong, et al. Mechanical responses and instability failure mechanisms of surrounding rock of tunnels in boulder-cobble mixed stratum［J］. Chinese Journal of Rock Mechanics and Engineering, 2021, 40（8）: 1643 − 1653. （in Chinese with English abstract）
[3] 岳中琦. 梅大高速公路路基边坡失稳条件与滑坡机理初探[J]. 中国地质灾害与防治学报,2024,35(4):1 − 12. [YUE Zhongqi. Study on the instability condition and landslide mechanism of subgrade slope in Mei–Da Expressway[J]. The Chinese Journal of Geological Hazard and Control,2024,35(4):1 − 12. (in Chinese with English abstract)] YUE Zhongqi. Study on the instability condition and landslide mechanism of subgrade slope in Mei–Da Expressway［J］. The Chinese Journal of Geological Hazard and Control, 2024, 35（4）: 1 − 12. （in Chinese with English abstract）
[4] 胡炜, 谭信荣, 蒋尧, 等. 深埋顺层偏压隧道围岩破坏机理及规律研究——以郑万线某隧道为例[J]. 水文地质工程地质,2020,47(3):60 − 68. [HU Wei, TAN Xinrong, JIANG Yao, et al. A study of the mechanism and regularity of failures in the surrounding rock of a deep buried bias tunnel embedded in geologically bedding strata: Taking one tunnel of the Zhengwan line as an example[J]. Hydrogeology & Engineering Geology,2020,47(3):60 − 68. (in Chinese with English abstract)] HU Wei, TAN Xinrong, JIANG Yao, et al. A study of the mechanism and regularity of failures in the surrounding rock of a deep buried bias tunnel embedded in geologically bedding strata: Taking one tunnel of the Zhengwan line as an example［J］. Hydrogeology & Engineering Geology, 2020, 47（3）: 60 − 68. （in Chinese with English abstract）
[5] 杜建明,房倩. 考虑黏聚力与内摩擦角的变坡面浅埋偏压隧道围岩压力计算方法[J]. 湖南大学学报(自然科学版),2022,49(1):165 − 173. [DU Jianming,FANG Qian. Calculation method of surrounding rock pressure of shallow-buried and asymmetrical pressure tunnel under variable slopes considering cohesion and internal friction angle[J]. Journal of Hunan University (Natural Sciences),2022,49(1):165 − 173. (in Chinese with English abstract)] DU Jianming, FANG Qian. Calculation method of surrounding rock pressure of shallow-buried and asymmetrical pressure tunnel under variable slopes considering cohesion and internal friction angle［J］. Journal of Hunan University （Natural Sciences）, 2022, 49（1）: 165 − 173. （in Chinese with English abstract）
[6] 康永水,耿志,刘泉声,等. 我国软岩大变形灾害控制技术与方法研究进展[J]. 岩土力学,2022,43(8):2035 − 2059. [KANG Yongshui,GENG Zhi,LIU Quansheng,et al. Research progress on support technology and methods for soft rock with large deformation hazards in China[J]. Rock and Soil Mechanics,2022,43(8):2035 − 2059. (in Chinese with English abstract)] KANG Yongshui, GENG Zhi, LIU Quansheng, et al. Research progress on support technology and methods for soft rock with large deformation hazards in China［J］. Rock and Soil Mechanics, 2022, 43（8）: 2035 − 2059. （in Chinese with English abstract）
[7] 严涛,李坤杰,牟智恒,等. 变坡条件下浅埋偏压隧道围岩压力解析法[J]. 西南交通大学学报,2020,55(3):531 − 536. [YAN Tao,LI Kunjie,MOU Zhiheng,et al. Analytical method for calculation of surrounding rock pressure of shallow-buried and unsymmetrically loaded tunnel adjacent to variable slope[J]. Journal of Southwest Jiaotong University,2020,55(3):531 − 536. (in Chinese with English abstract)] YAN Tao, LI Kunjie, MOU Zhiheng, et al. Analytical method for calculation of surrounding rock pressure of shallow-buried and unsymmetrically loaded tunnel adjacent to variable slope［J］. Journal of Southwest Jiaotong University, 2020, 55（3）: 531 − 536. （in Chinese with English abstract）
[8] 池建军,刘登学,丁秀丽,等. 第三系泥岩隧洞围岩大变形成因及应对措施[J]. 长江科学院院报,2022,39(10):88 − 96. [CHI Jianjun,LIU Dengxue,DING Xiuli,et al. Causes and countermeasures of large deformation in a tunnel with tertiary mudstone[J]. Journal of Yangtze River Scientific Research Institute,2022,39(10):88 − 96. (in Chinese with English abstract)] DOI: 10.11988/ckyyb.20211286 CHI Jianjun, LIU Dengxue, DING Xiuli, et al. Causes and countermeasures of large deformation in a tunnel with tertiary mudstone［J］. Journal of Yangtze River Scientific Research Institute, 2022, 39（10）: 88 − 96. （in Chinese with English abstract） DOI: 10.11988/ckyyb.20211286
[9] 张广泽,邓建辉,王栋,等. 隧道围岩构造软岩大变形发生机理及分级方法[J]. 工程科学与技术,2021,53(1):1 − 12. [ZHANG Guangze,DENG Jianhui,WANG Dong,et al. Mechanism and classification of tectonic-induced large deformation of soft rock tunnels[J]. Advanced Engineering Sciences,2021,53(1):1 − 12. (in Chinese with English abstract)] ZHANG Guangze, DENG Jianhui, WANG Dong, et al. Mechanism and classification of tectonic-induced large deformation of soft rock tunnels［J］. Advanced Engineering Sciences, 2021, 53（1）: 1 − 12. （in Chinese with English abstract）
[10] 杜建明,房倩,海路,等. 地表变坡下浅埋偏压隧道围岩压力计算方法[J]. 中南大学学报(自然科学版),2021,52(11):4088 − 4098. [DU Jianming,FANG Qian,HAI Lu,et al. Calculation method for surrounding rock pressure of shallow tunnel with asymmetrical pressure of variable slopes[J]. Journal of Central South University (Science and Technology),2021,52(11):4088 − 4098. (in Chinese with English abstract)] DU Jianming, FANG Qian, HAI Lu, et al. Calculation method for surrounding rock pressure of shallow tunnel with asymmetrical pressure of variable slopes［J］. Journal of Central South University （Science and Technology）, 2021, 52（11）: 4088 − 4098. （in Chinese with English abstract）
[11] 邵江,朱宝龙,李涛. 不同滑带角度滑坡作用下隧道衬砌结构受力特征[J]. 西南交通大学学报,2021,56(6):1214 − 1221. [SHAO Jiang,ZHU Baolong,LI Tao. Stress characteristics of tunnel lining structures under landslides with different angles of sliding zone[J]. Journal of Southwest Jiaotong University,2021,56(6):1214 − 1221. (in Chinese with English abstract)] SHAO Jiang, ZHU Baolong, LI Tao. Stress characteristics of tunnel lining structures under landslides with different angles of sliding zone［J］. Journal of Southwest Jiaotong University, 2021, 56（6）: 1214 − 1221. （in Chinese with English abstract）
[12] 董建华,颉永斌,李建军,等. 洞口段浅埋偏压隧道新型防护结构及其简化计算方法[J]. 中国公路学报,2018,31(10):339 − 349. [DONG Jianhua,XIE Yongbin,LI Jianjun,et al. New protective structure for shallow-buried bias tunnel at portal section and its simplified calculation method[J]. China Journal of Highway and Transport,2018,31(10):339 − 349. (in Chinese with English abstract)] DOI: 10.3969/j.issn.1001-7372.2018.10.034 DONG Jianhua, XIE Yongbin, LI Jianjun, et al. New protective structure for shallow-buried bias tunnel at portal section and its simplified calculation method［J］. China Journal of Highway and Transport, 2018, 31（10）: 339 − 349. （in Chinese with English abstract） DOI: 10.3969/j.issn.1001-7372.2018.10.034
[13] LI Biao,DING Quanfu,XU Nuwen,et al. Characteristics of microseismic b-value associated with rock mass large deformation in underground powerhouse Caverns at different stress levels[J]. Journal of Central South University,2022,29(2):693 − 711. DOI: 10.1007/s11771-022-4946-4
[14] MA Lin. Analysis of shallow bias tunnel influence factors in mountain area[J]. International Congress of Mathematicans,2015.
[15] 孔超,张俊儒,王海彦,等. 深埋软岩大变形隧道支护变形特征及承载机理研究[J]. 中国铁道科学,2021,42(6):103 − 111. [KONG Chao,ZHANG Junru,WANG Haiyan,et al. Study on deformation characteristics and bearing mechanism of support in large deformation tunnel with deep buried soft rock[J]. China Railway Science,2021,42(6):103 − 111. (in Chinese with English abstract)] DOI: 10.3969/j.issn.1001-4632.2021.06.11 KONG Chao, ZHANG Junru, WANG Haiyan, et al. Study on deformation characteristics and bearing mechanism of support in large deformation tunnel with deep buried soft rock［J］. China Railway Science, 2021, 42（6）: 103 − 111. （in Chinese with English abstract） DOI: 10.3969/j.issn.1001-4632.2021.06.11
[16] 陈秋雨, 黄璐, 潘虎, 等. 径向让压系统对软岩隧道围岩力学特性影响研究[J]. 水文地质工程地质,2024,51(4):146 − 156. [CHEN Qiuyu, HUANG Lu, PAN Hu, et al. Enhancing mechanical characteristics of soft rock tunnel surrounding rock through radial yield pressure system[J]. Hydrogeology and Engineering Geology,2024,51(4):146 − 156. (in Chinese with English abstract)] CHEN Qiuyu, HUANG Lu, PAN Hu, et al. Enhancing mechanical characteristics of soft rock tunnel surrounding rock through radial yield pressure system［J］. Hydrogeology and Engineering Geology, 2024, 51（4）: 146 − 156. （in Chinese with English abstract）
[17] 陈东旭. 新奥法隧道支护结构约束效应及破裂失效模型研究[D]. 阜新:辽宁工程技术大学,2021. [CHEN Dongxu. Study on constraint effect and rupture failure model of new Austrian method tunnel support structure[D]. Fuxin:Liaoning Technical University,2021. (in Chinese with English abstract)] CHEN Dongxu. Study on constraint effect and rupture failure model of new Austrian method tunnel support structure［D］. Fuxin: Liaoning Technical University, 2021. （in Chinese with English abstract）
[18] 孙闯,敖云鹤,张家鸣. 弱节理小净距隧道合理净距及围岩稳定性研究[J]. 公路交通科技,2020,37(5):108 − 115. [SUN Chuang,AO Yunhe,ZHANG Jiaming. Study on reasonable clear distance and surrounding rock stability of weak jointed small clear distance tunnel[J]. Journal of Highway and Transportation Research and Development,2020,37(5):108 − 115. (in Chinese with English abstract)] SUN Chuang, AO Yunhe, ZHANG Jiaming. Study on reasonable clear distance and surrounding rock stability of weak jointed small clear distance tunnel［J］. Journal of Highway and Transportation Research and Development, 2020, 37（5）: 108 − 115. （in Chinese with English abstract）
[19] HOEK E,BROWN E T. Practical estimates of rock mass strength[J]. International Journal of Rock Mechanics and Mining Sciences,1997,34(8):1165 − 1186. DOI: 10.1016/S1365-1609(97)80069-X
[20] ALEJANO L R,RODRIGUEZ-DONO A,ALONSO E,et al. Ground reaction curves for tunnels excavated in different quality rock masses showing several types of post-failure behaviour[J]. Tunnelling and Underground Space Technology,2009,24(6):689 − 705. DOI: 10.1016/j.tust.2009.07.004
计量
- 文章访问数: 54
- HTML全文浏览量: 6
- PDF下载量: 31
邮件订阅
RSS