Evolution of the characteristic parameters of acoustic emission from deformation to failure of a loose soil slope
-
摘要:
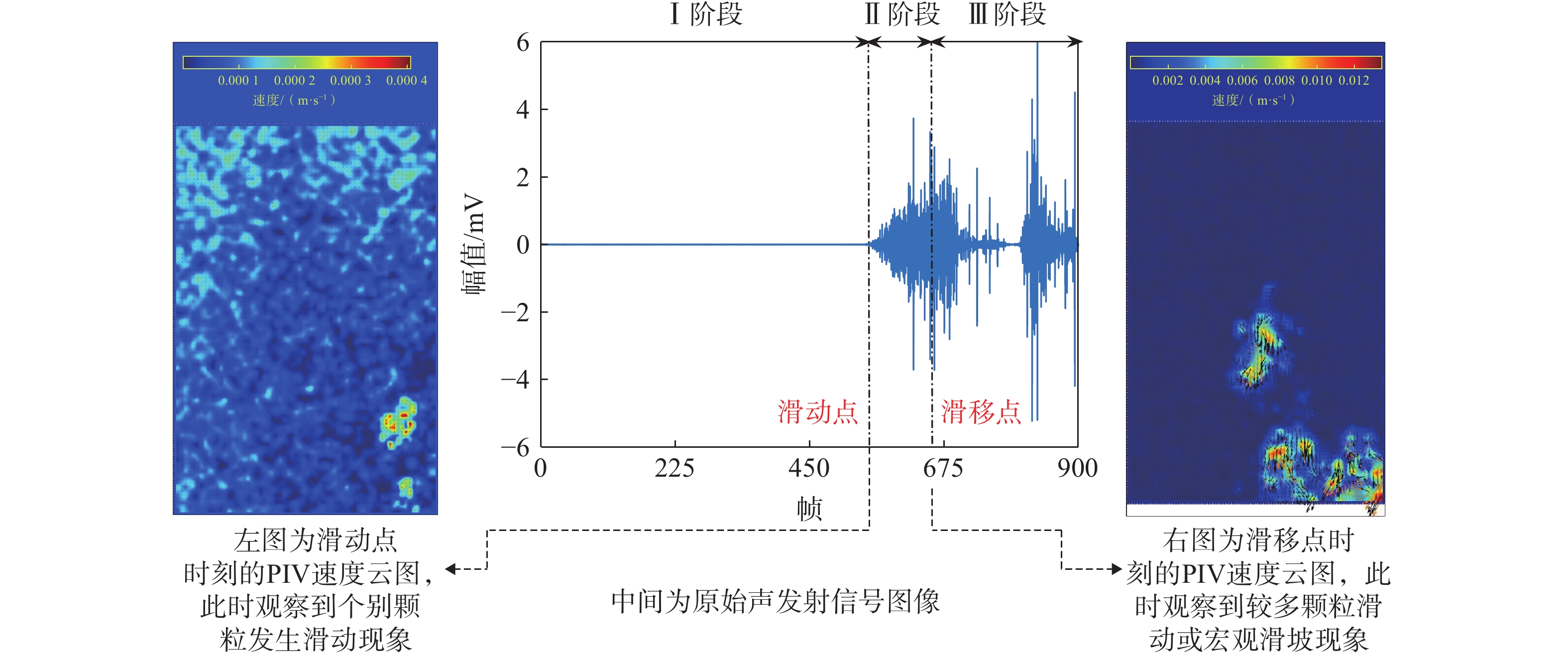
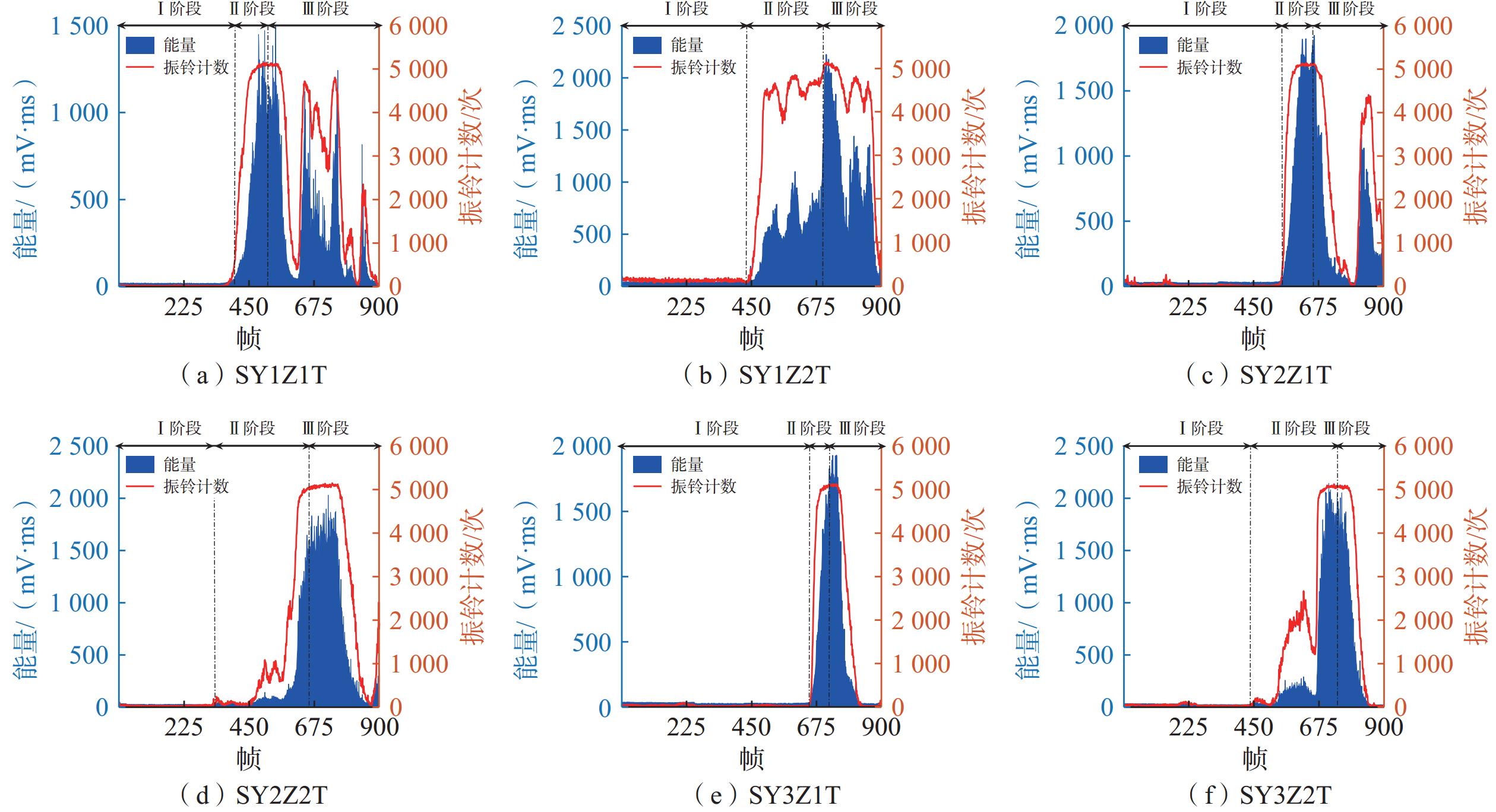
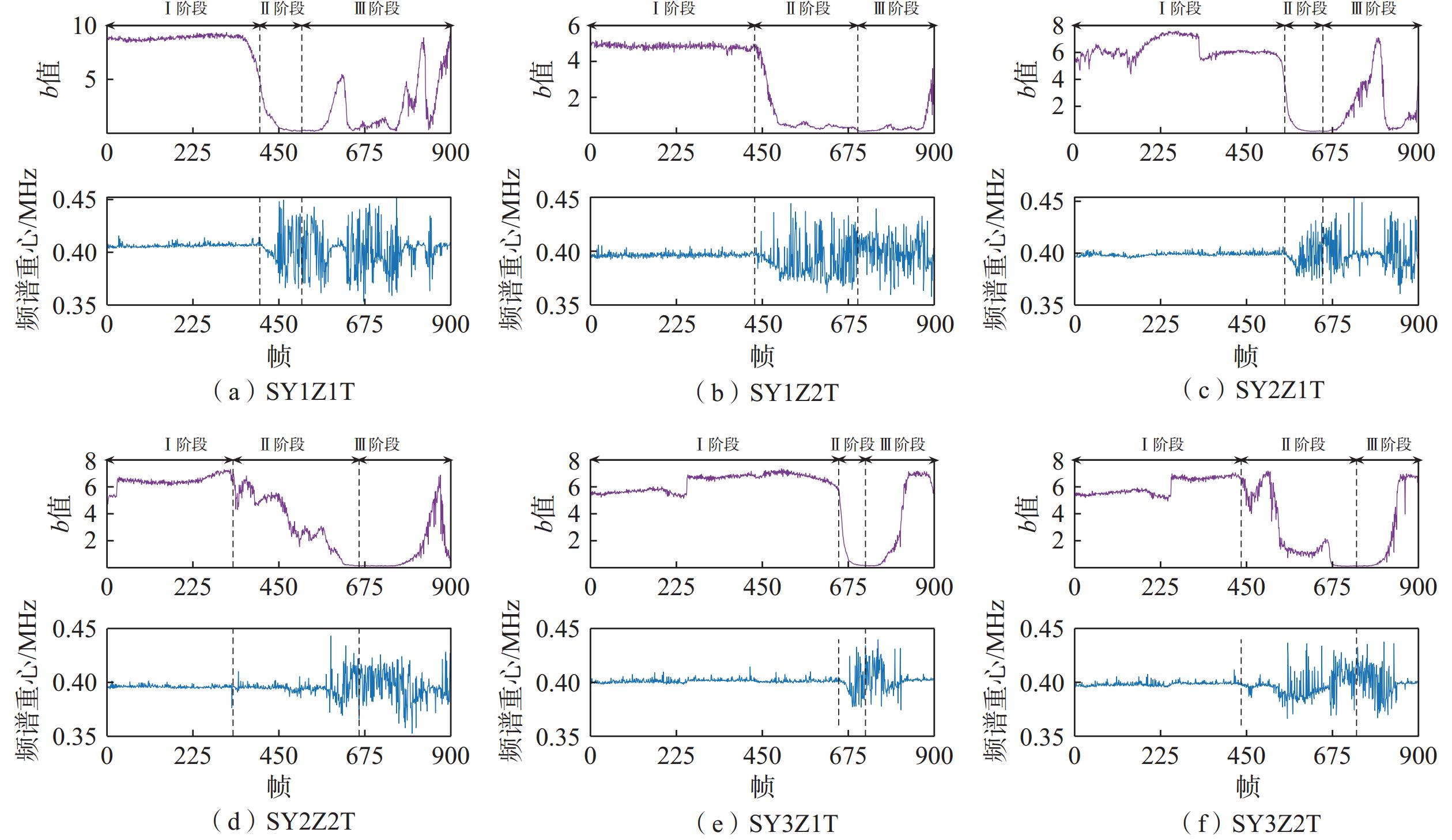
松散堆积体在自然界和工业生产中广泛存在，有复杂的力学性质和相对较高的失稳风险。为研究其在斜坡变形中的滑移失稳过程，基于声发射技术探究了松散体从静止、蠕变到滑移整个过程中声学特征演化规律。分析松散体在滑移过程中的声发射特征（acoustic emission，AE）参数，然后结合松散体的状态变化对AE演化阶段进行了划分，最后结合颗粒图像测速法（particle image velocimetry，PIV）分析和频谱变化进一步验证了松散体滑移过程的AE演化规律。结果表明：振铃计数和能量随滑移过程而逐渐增大，b值（小事件数与大事件数的比值）随滑移过程逐渐降低，b值、振铃计数和能量的滑移门槛值为0.2、
5000 次和1500 mV·ms，其中b值对松散体的状态变化更敏感；频谱重心在临滑移前期有30～50 kHz的降幅，而后发生震荡变化，其震荡时间区域正好对应振铃计数和能量数值相对较高及b值相对较低的时间区域；此外松散体滑移前存在一个重要的“窗口期”，说明AE技术具有识别松散体滑坡前兆的潜力。Abstract:Loose accumulations are widely present in nature and industrial production, possessing complex mechanical properties and relatively high risks of instability. To investigate their sliding instability process during slope deformation, this study explores the evolution of acoustic characteristics throughout the entire process of loose accumulations, from static state, creep to sliding, based on acoustic emission (AE) technology. The AE characteristic parameters of loose accumulations during the sliding process are analyzed, and the AE evolution stages are divided based on the state changes of loose accumulations. Finally, the AE evolution law of the sliding process of loose accumulations is further verified through particle image velocimetry (PIV) analysis and spectral changes. The results indicate that the ringing count and energy gradually increase with the sliding process, while the b-value gradually decreases. The sliding threshold values for the b-value, ringing count, and energy are 0.2,
5000 counts, and1500 mV·ms, respectively, with the b-value being more sensitive to state changes in loose accumulations. The spectral centroid experiences a decrease of 30～50 kHz in the early pre-sliding stage, followed by oscillatory changes. The time period of these oscillations corresponds to relatively high ringing count and energy values and relatively low b-values. Furthermore, there is an important “window period” before the sliding of loose accumulations, indicating that AE technology has the potential to identify precursors of loose accumulation landslides.-
Keywords:
- acoustic emission /
- loose accumulations /
- landslide monitoring /
- slip processes /
- PIV
-
0. 引言
地基稳定性受多种因素影响[1 − 2]，特别是黄土地区，受震陷影响很大。黄土震陷作为一种严重的地质灾害，一旦发生将会造成非常严重的后果。前人对与黄土震陷的研究基本是以动三轴试验为主，以单个震陷量作为震陷性的主要的评价指标[3 − 6]。然而黄土地基震陷的准确性评价受到土性参数不确定性的影响，其中物理力学指标的概率分布类型和变异性会对评价结果产生影响。针对岩土工程中参数、计算模型、荷载等不确定性问题，其主要的不确定性分析方法包括：概率分析方法[7]、随机有限元法[8]、灰色系统评价法[9]、模糊数学法[10]、神经网络评价方法[11]等。这些不确定性方法可以考虑得更加全面，从而提高评价结果的准确性，使结果更为科学合理。
关于黄土震陷在不确定性方面的研究，李波等[12]采用灰色关联方法和逐步判别方法建立了耦合式软土震陷判别模型从而实现软土震陷等级的判定。在黄土震陷概率评价方面，谭芳[13]将概率地震危险性分析方法引入震陷计算中，采用不确定性分析方法分析了黄土震陷与地震参数之间的关系，从而提出一种考虑地震随机性的黄土震陷预测方法。任森等[14]基于大量动三轴试验，结合场地地震危险性概率分析方法，确定了研究区内的震陷区划。孙军杰等[15]依据残余应变估算模型采用概率统计等非确定性分析方法对地基动力沉降进行了概率分析。可见概率分析方法在土体动力沉降中已经得到了初步研究。
然而到目前为止，还没有研究将可靠度理论应用于黄土地基震陷的分析中。因此本文尝试将可靠度理论应用于黄土地基震陷评价中，使用可靠度方法对黄土地基震陷性进行分析。可靠度方法和传统的确定性分析方法相互补充与结合，有助于进行震陷可靠度分析。
1. 黄土地基震陷可靠度指标
可靠度理论在边坡稳定分析中被广泛应用，而边坡工程的不确定因素主要为土体参数的抗剪强度（内摩擦角、黏聚力）[16 − 18]。其依托蒙特卡洛分析法通过计算出多组安全系数值将小于1的安全系数的次数与计算次数的比值称作失效概率。因此可求得对应的可靠度指标（$ \mathrm{\beta } $）为：
$$ \beta ={\varPhi }^{-1}(1-{P}_{\text{f}}) $$ (1) 式中：$ \varPhi $——标准正态分布的累计分布函数；
${P_{\text{f}}}$——失效概率。
在目前已有的地震灾害评估中，尚未有关于地基震陷量的标准划分依据。根据中国地震局发布的《震害调查及地震损失评定工作指南》，可以采用“地基基础破坏等级标准”来评估震陷灾害的程度[16]，将震陷量小于2 cm的定义为基本完好，震陷量大于40 cm的定义为破坏。
参考可靠度理论在边坡稳定性评价中的应用，结合黄土动力学对震陷等级的划分，本文提出了一种对黄土地基震陷评价的可靠度指标。
（1）最大可靠度
在震陷等级划分中将震陷量大于40 cm的定义为震陷破坏，因此可采用破坏概率（Pd）来判定其震陷破坏状态，即$ {P_{\mathrm{d}}} = P\left( {S \geqslant 40} \right) $。将$ \beta_{\mathrm{d}} $定义为：
$$ {\beta _{\mathrm{d}}} = \frac{{40 - {u_{\mathrm{s}}}}}{{{\sigma _{\mathrm{s}}}}} $$ (2) 式中：$ {u_{\mathrm{s}}} $——震陷量的平均值；
$ {\sigma _{\mathrm{s}}} $——震陷量的标准差。
如果震陷量符合标准正态分布，破坏概率与可靠度的关系可表示为：
$$ {P_{\mathrm{d}}} = P\left( {S > 40} \right) = 1 - \varPhi \left(\frac{{40 - {u_{\mathrm{s}}}}}{{{\sigma _{\mathrm{s}}}}}\right) = 1 - \varPhi ({\beta _{\mathrm{d}}}) $$ (3) 则根据可靠度理论，将破坏概率对应的可靠度称为最大可靠度（${\beta }_{\text{d}} $），也就是指衡量地基震陷最大安全程度的标准，其计算公式为：
$$ {\beta }_{\text{d}}={\varPhi }^{-1}(1-{P}_{\text{d}}) $$ (4) 根据蒙特卡罗可靠度计算方法可定义破坏概率为：
$$ {P_{\text{d}}} = \frac{M}{N} $$ (5) 式中：$ {P}_{{\mathrm{d}}} $——地基震陷破坏概率；
M——抽样次数中震陷量大于40 cm的次数；
N——蒙特卡洛分析法总的抽样次数。
（2）最小可靠度
在震陷等级划分中将震陷量小于2 cm的定义为基本完好，因此可采用完好概率（Ph）来判定其完好状态，即$ {P_{\mathrm{h}}} = P\left( {S \leqslant 2} \right) $。将$ {\beta _{\mathrm{h}}} $定义为：
$$ {\beta _{\mathrm{h}}} = \frac{{2 - {u_{\mathrm{s}}}}}{{{\sigma _{\mathrm{s}}}}} $$ (6) 式中：$ {u_{\mathrm{s}}} $——震陷量的平均值；
$ {\sigma _{\mathrm{s}}} $——震陷量的标准差。
如果震陷量符合标准正态分布，完好概率（Ph）与可靠度的关系可表示为：
$$ {P_{\mathrm{h}}} = P\left( {S < 2} \right) = \varPhi \left(\frac{{2 - {u_{\mathrm{s}}}}}{{{\sigma _{\mathrm{s}}}}}\right) = \varPhi ({\beta _{\mathrm{h}}}) $$ (7) 根据可靠度理论，将完好概率对应的可靠度称为最小可靠度（${\beta _{\mathrm{h}}} $），也就是指衡量地基震陷完好程度的标准，其计算公式为：
$$ {\beta _{\text{h}}} = {\varPhi ^{ - 1}}\left( {{P_{\text{h}}}} \right) $$ (8) 根据蒙特卡罗可靠度计算方法可定义完好概率为：
$$ {P_{\text{h}}} = \frac{M}{N} $$ (9) 式中：$ {P}_{{\mathrm{h}}} $——地基完好概率；
M——抽样次数中震陷量小于2 cm的次数；
N——蒙特卡洛分析法总的抽样次数。
2. 基于Kriging代理模型的震陷可靠度计算
2.1 Kriging代理模型的建立
Kriging模型是一种基于方差最小的无偏估计方法，它的原理是通过已知样本点的线性加权法来预测未知点的函数值，即已知加权系数插值就可求得变量空间内任一点的函数值。Kriging代理模型通常情况下由回归部分和随机误差两部分所组成。将其用输出变量S(x)与输入变量x表示为：
$$ S({\boldsymbol{x}}) = \sum\limits_{i = 1}^m {{\beta _i}} f({\boldsymbol{x}}) + {\textit{z}}({\boldsymbol{x}}) = f{({\boldsymbol{x}})^T}{\boldsymbol{\beta}} + {\textit{z}}({\boldsymbol{x}}) $$ (10) 式中：每个样本点中输入变量的个数为n，$ {\boldsymbol{x}} = [ {x_1},{x_2}, \cdots , {x_n} ]^T$，$ f(x) = {\left[ {{f_1}(x),{f_2}(x), \cdots ,{f_m}(x)} \right]^T} $为回归多项式基函数向量，m为回归多项式的数量；${\boldsymbol{\beta}} = {[{\beta _1},{\beta _2},\cdots,{\beta _m}]^T}$为多项式参数向量，z(x)为一均值为0，方差为$ {\sigma ^2} $的正态随机过程，该随机过程的协方差为：
$$ COV\left[{\textit{z}}(u),{\textit{z}}(v)\right]={\sigma }^{2}R({u,v}) $$ (11) 其中，R表示任意两点u，v的相关函数，通常取为高斯相关方程，即：
$$ R(u,v) = \exp \left\{ { - \theta {{(u - v)}^2}} \right\} $$ (12) 其中，$ \theta $为相关参数，可通过最大似然估计得到：
$$ \theta=\max \left\{ { - \left[ {\frac{1}{2}\ln \left( {\left| R \right|} \right)} \right] + \frac{k}{2}\ln \left( {{\sigma ^2}} \right)} \right\} $$ (13) 其中，R为相关矩阵，元素R=R(u,v)。
基于给定的样本点，多项式参数向量$\beta $与随机过程方差$ {\sigma ^2} $的估计值分别为：
$$ \left\{ {\begin{split} & {\hat {\boldsymbol{\beta}} = {{\left( {{{\boldsymbol{F}}^T}{{\boldsymbol{R}}^{ - 1}}{\boldsymbol{F}}} \right)}^{ - 1}}{{\boldsymbol{F}}^T}{{\boldsymbol{R}}^{ - 1}}{\boldsymbol{Y}}} \\ & {{{\hat {\boldsymbol{\sigma}} }^2} = \frac{1}{k}{{\left( {{\boldsymbol{Y}} - {\boldsymbol{F}}\hat {\boldsymbol{\beta}} } \right)}^T}{{\boldsymbol{R}}^{ - 1}}\left( {{\boldsymbol{Y}} -{\boldsymbol{ F}}\hat {\boldsymbol{\beta}} } \right)} \end{split}} \right. $$ (14) 其中，F为由回归多项式函数值构成的矩阵。
对于任意输入变量$ {x_0} $,假定$ {x_0} $与输入变量样本X之间的相关系数向量为$ {{\boldsymbol{r}}_0} = {\left[ {R\left( {{x_0},{x_1}} \right), \cdots ,R\left( {{x_0},{x_k}} \right)} \right]^T} $利用式（10）构建的Kriging模型表达式，可以得到与$ {x_0} $对应的系统响应值$ S({x_0}) $的预测值$ \hat S({x_0}) $服从正态分布$ N(\hat S({x_0}),{\hat \sigma _{\hat S}}^2({x_0})) $,$ S({x_0}) $的最佳线性无偏估计及均方误差可表示为：
$$ \left\{ {\begin{split} &{\hat S\left( {{x_0}} \right) = {f^T}({x_0})\hat {\boldsymbol{\beta}} + {{\boldsymbol{r}}_0}^T{{\boldsymbol{R}}^{ - 1}}({\boldsymbol{Y}} - {\boldsymbol{F}}\hat {\boldsymbol{\beta }})} \\ & {{{\hat \sigma }^2}_{\hat S}({x_0}) = {{\hat \sigma }^2}\left( {1 + {{\boldsymbol{u}}^T}{{({{\boldsymbol{F}}^T}{{\boldsymbol{R}}^{ - 1}}{\boldsymbol{F}})}^{ - 1}}{\boldsymbol{u}} - {{\boldsymbol{r}}_0}^T{{\boldsymbol{R}}^{ - 1}}{{\boldsymbol{r}}_0}} \right)} \end{split}} \right. $$ (15) 其中，$ {{{\boldsymbol{u}} = }}{{{{\boldsymbol{F}}}}^T}{{\boldsymbol{R}}^{ - 1}}{{\boldsymbol{r}}_0} - {\boldsymbol{f}} $。
本文进行震陷可靠度分析时，式（10）—（15）中应用Kriging模型构建和预测其过程，采用MATLAB中的DACE工具箱实现。
2.2 黄土地基数值模型
采用FLAC3D有限差分软件建立黄土地基数值模型，模型尺寸设置为15 m×15 m×15 m，模型网格数为
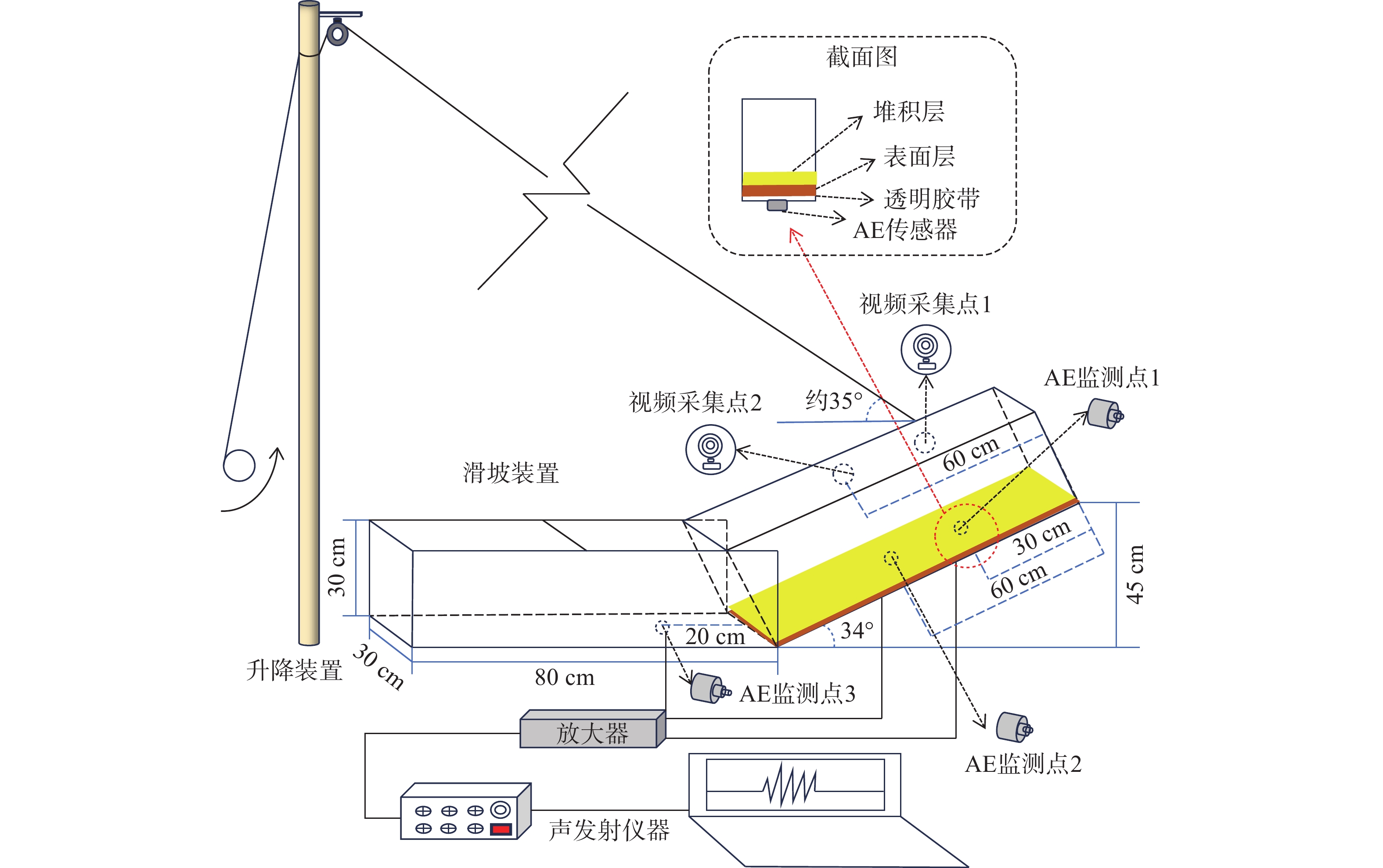
3375 ，本构模型选择Mohr-Coulomb弹塑性本构模型。在静力分析时，底面和侧面选用固定边界，限制底面与侧面的位移和速度，顶部为自由边界。动力分析与静力分析不同，由于地震荷载会存在波的反射，因此在模型底面设置静态边界，侧面设置为自由场边界，模拟土体在实际中的状态（图1）。本文选用三条地震波分别是Kobe地震波、Imperial地震波和一条人工合成波。为方便后续说明，这里将选用的三条地震波分别命名为地震波1、地震波2及地震波3。地震波1的持续时间为25 s，时间间隔为0.02 s，最大加速度为0.345g，地震波2的持续时间为40 s，时间间隔为0.01 s，最大加速度为0.313g，地震波3的持续时间为20 s，时间间隔为0.02 s，最大加速度为0.153g。图2为经过滤波以及基线校正后所选地震波的时程曲线。
为了研究不同地震水平作用下震陷变形规律，将其改变幅值的大小来满足不同工况的需要，得到 0.1g、0.2g、0.3g、0.4g、0.5g、0.6g、0.7g不同峰值加速度大小的7种水平。其计算所得震陷量结果如表1所示。
表 1 不同地震波及不同峰值加速度作用下地基震陷量Table 1. Seismic subsidence of foundation under different seismic waves and peak accelerations.峰值加速度/g 震陷量/cm 地震波1 地震波2 地震波3 0.1 0.72 1.95 2.65 0.2 2.37 8.40 13.44 0.3 9.10 16.02 21.62 0.4 17.83 21.44 29.52 0.5 19.78 25.29 37.06 0.6 20.08 30.67 40.98 0.7 20.48 35.84 46.98 2.3 震陷变形影响因素敏感性分析
岩土体材料参数存在着变异性，但土体泊松比的变异系数非常小，在考虑土性参数不确定时可将其看作常量。孙军杰等[17]通过理论分析，给出了非饱和黄土动残余应变与黏聚力、内摩擦角、初始孔隙比、土层重度、土层埋深以及地震动荷载之间的定量关系式。压缩模量是体现土体压缩性的指标之一，作为土体的力学性质，在分析地基土体变形或沉降时起着重要作用，而土体的黏聚力和内摩擦角反映土体的强度特征，在静力分析中，黄土地基静力参数中密度对于计算结果的影响较明显。因此，这里选择密度、弹性模量、黏聚力及内摩擦角四种参数。采用FLAC3D结合灰色关联分析对影响黄土地基震陷变形的因素做敏感性分析，求得其密度、弹性模量、黏聚力及摩擦角四个参数的灰色关联度为$ q = [ {0.656\;8},\;{0.856\;2},\;{0.668\;5},\;{0.728\;1} ] $，敏感性排序为：弹性模量>内摩擦角>黏聚力>密度。
2.4 土性参数分布概率模型
本节选取密度（ρ）、压缩模量（Es）、黏聚力（c）及内摩擦角（φ）四种参数作为黄土震陷性评价的参数指标来进行分布概率模型研究。为了全面分析不同地貌单元4种土性参数的最优概率分布，选用可以包含大部分不确定性因素的概率分布形式包括正态分布、对数正态分布和威布尔分布进行假设检验。从而确定每个参数的最优概率分布形式[18]。
为获取原状黄土地基土性不同参数的分布概率模型，基于引汉济渭工程的渭河二级阶地地貌土体为例，通过对原状黄土的各种物理力学指标进行统计分析，得出各指标服从的概率密度函数及分布参数，图3所示为渭河二级阶地分布概率模型图，其中$ f\left( x \right) $表示概率密度函数。
![]()
图 3 不同参数的概率密度分布图Figure 3. Probability density distribution plots of different parameters由图3可知，从分布形态上来看，$ \rho $值的正态分布和对数正态分布整体较一致，两者均属于左偏态；其余三种土性参数正态分布、对数正态分布及威布尔分布三者分布较离散，差异性较大。
通过K-S检验法对4种土性参数的3种分布概率模型进行检验，求出样本值的理论累计概率分布与经验累计概率分布的最大差值（Dmax），与由显著性水平和样本数确定临界值（$ D_n^\alpha $）进行比较，计算结果如表2所示。四种参数均可接受正态分布、对数正态分布和威布尔分布。$ c $、$ {E_{\mathrm{s}}} $值的最优分布是正态分布，$ \varphi $、$ \rho $值的最优分布是威布尔分布，考虑到正态分布的优良性质，将正态分布作为4种土性参数的分布概率模型用于震陷可靠度计算。
表 2 分布假设检验结果Table 2. Distribution hypothesis test results检验参数 样本量 验证结果$ {D_{\max }} $ 可接受的临界值
$ D_n^\alpha /\left( {\alpha = 0.05} \right) $正态分布 对数正态分布 威布尔分布 结果 $ {D_{\max }} $ 结果 $ {D_{\max }} $ 结果 $ {D_{\max }} $ 内摩擦角 24 √ 0.180 √ 0.223 √ 0.093 0.273 黏聚力 24 √ 0.099 √ 0.125 √ 0.102 0.273 压缩模量 24 √ 0.094 √ 0.146 √ 0.164 0.273 密度 48 √ 0.150 √ 0.185 √ 0.115 0.196 2.5 基于Kriging代理模型的震陷可靠度计算方法
本节基于Kriging代理模型对地基震陷可靠度进行计算，这里进行
10000 次模拟，计算步骤如下：（1）根据前文统计出的土性参数（密度、压缩模量、黏聚力、摩擦角）的概率分布模型，确定地基土体参数的均值、标准差、分布类型等统计特性。
（2）FLAC3D6.0内置有Python编程语言，可以实现蒙特卡洛抽样与连续计算，利用Itasca开发的专门用于Python扩展编程的程序库，通过编程实现随机变量拉丁超立方抽样（LHS）、模型的建立以及计算，即会产生N组计算方案$ \left(\rho_1,E_{\mathrm{s}1},c_1,\varphi_1\right),\left(\rho_2,E_{\mathrm{s}2},c_2,\varphi_2\right),\cdots,(\rho_n,E_{\mathrm{s}n},c_n, \varphi_n) $，然后计算出对应的响应值。将计算模型文件保存为“n.f3sav”，后续模型按顺序编号，并将其作为源文件以便后续提取。
（3）对地震波设计不同的工况组合，计算每组工况下LHS的样本所对应的震陷量，并保存计算模型。
（4）利用Python编程语言从结果文件中批量提取竖向变形。
（5）采用MATLAB软件分别建立不同工况下的Kriging代理模型，以4种土体参数为输入，相应的地基震陷量为输出，对代理模型进行训练，得到满足精度要求的代理模型。经适当训练的代理模型能够较好地逼近实际情况，在此基础上可以十分方便地预测震陷值从而实现震陷可靠度的计算（图4）。
![]()
图 4 基于Kriging代理模型的震陷可靠度计算流程Figure 4. Calculation process of seismic subsidence reliability based on the Kriging surrogate model3. 算例分析
为验证本文提出方法的适用性，本节以引汉济渭工程为背景结合Kriging代理模型的震陷概率计算方法开展黄土地基震陷可靠度分析。
（1）最大可靠度
表3为不同地震波及不同地震峰值加速度作用下地基震陷的破坏概率，以渭河二级阶地为例。
表 3 不同地震波作用下地基震陷破坏概率Table 3. Probability of foundation subsidence failure under different seismic wave effects加速度/g 地震波1 地震波2 地震波3 0.1 0 0 0 0.2 0 0 0 0.3 0 0 0 0.4 0 0.072 0.116 0.5 0 0.17 0.378 0.6 0 0.232 0.704 0.7 0.002 0.264 0.888 由表3可知，在地震波1的作用下，该地基土体在地震波峰值加速度为0.7g时会出现破坏的概率，在地震波2和地震波3的作用下，在峰值加速度达到0.4g时会出现破坏的概率。三条地震波在峰值加速度达到最大时，其产生的破坏概率也有巨大差异，地震波1在峰值加速度为0.7g时破坏概率为0.002，地震波2在峰值加速度为0.7g时破坏概率为0.264，地震波3在峰值加速度为0.7g时破坏概率为0.888。
依据式（4）求得最大可靠度指标，图5为不同地震波作用下地基震陷的可靠度指标随峰值加速度的变化规律，最大可靠度指标的范围为−1.216～4.526。总体上可靠度指标随峰值加速度的增加呈非线性减小。但三条地震波的减小斜率并不相同，在地震波3作用下，可靠度指标随峰值加速度的变化斜率最大，说明在地震波3作用下，地基的可靠度受地震波峰值加速度的影响最大。对于已知地震波峰值加速度，可以快速粗略估计地基震陷的破坏概率，而不是单纯以震陷量来评价，这在风险评估中具有更为重要的意义。
![]()
图 5 可靠度分析获得的地基震陷最大可靠度Figure 5. Maximum reliability index of foundation seismic subsidence obtained from reliability analysis（2）最小可靠度
表4为不同地震波及不同地震峰值加速度作用下地基震陷的破坏概率，以渭河二级阶地为例。由表4可知，在地震波1的作用下，该地基土体在地震波峰值加速度为0.1g～0.7g时均会出现完好概率，在地震波2和地震波3的作用下，在峰值加速度分别达到0.4g及以后和0.3g及以后完好概率均为0。
表 4 不同地震波作用下地基震陷完好概率Table 4. Probability of intact seismic subsidence of foundation under different seismic wave effects加速度/g 地震波1 地震波2 地震波3 0.1 0.946 0.854 0.842 0.2 0.392 0.094 0.832 0.3 0.238 0.004 0 0.4 0.01 0 0 0.5 0.018 0 0 0.6 0.012 0 0 0.7 0.002 0 0 依据式（8）求得最小可靠度指标，图6为在不同地震波作用下地基震陷的最小可靠度随峰值加速度的变化规律，最小可靠度指标的变化范围为−2.878～1.607。从整体来说，随着地震峰值加速度的增大，地基在地震作用下的最小可靠度指标逐渐降低。当地震峰值加速度为0.1g时，震陷最小可靠度较高，都为正值；当地震峰值加速度为0.2g时，地震最小可靠度显著减小，且超过0.2g以后最小可靠度均为负值。
![]()
图 6 可靠度分析获得的地基震陷的最小可靠度指标Figure 6. Minimum reliability index of foundation seismic subsidence obtained from reliability analysis（3）变异系数对震陷可靠度的影响
为了更好地分析随机变量的变异性大小对震陷可靠度的影响，本文计算了各变量在不同变异系数组合情况下，四种土体参数变异系数随地基震陷可靠度的变化情况，工况组合见表5。
表 5 各参数变异系数工况组合表Table 5. Combination table of variation coefficient for each parameter工况 COV 密度 弹性模量 黏聚力 摩擦角 1-1 0.01 0.3 0.2 0.3 1-2 0.05 1-3 0.1 1-4 0.15 1-5 0.2 2-1 0.05 0.05 0.2 0.3 2-2 0.1 2-3 0.2 2-4 0.3 2-5 0.4 3-1 0.05 0.3 0.05 0.3 3-2 0.1 3-3 0.2 3-4 0.3 3-5 0.4 4-1 0.05 0.3 0.2 0.1 4-2 0.2 4-3 0.3 4-4 0.4 4-5 0.5 计算结果如图7所示。由图可知，随各参数变异系数的增加，震陷最大可靠度逐渐减小，而最小可靠度逐渐增大。当$ COV(\rho) $从0.01增加至0.2，相应的$ {\beta _{\text{d}}} $从3.72减小至3.05，最小可靠度（$ {\beta _{\text{h}}} $）从−1.72增加至−1.55，降幅为21.97%，增幅为10.96%；当$ COV(E_{\mathrm{s}}) $从0.05增加至0.4，相应的$ {\beta _{\text{d}}} $从3.89降至3.29，$ {\beta _{\text{h}}} $从−1.89增加至−1.64，降幅为18.24%，增幅为15.24%；当$ COV(c) $从0.05增加至0.4，$ {\beta _{\text{d}}} $从4.26降至2.89，$ {\beta _{\text{h}}} $从−1.81增加至−1.60，降幅为47.40%，增幅为13.13%；当$ COV(\varphi)$从0.1增加至0.5，$ {\beta _{\text{d}}} $从3.72降至2.74，$ {\beta _{\text{h}}} $从−1.99增加至−1.63，降幅为35.77%，增幅为22.09%。对比数据，在同样的增幅下，最大可靠度的变化幅度比最小可靠度的变化幅度大说明最大可靠度对变异系数更为敏感。计算各个参数最大可靠度起末两点斜率的绝对值，分别为3.526、1.714、3.914和2.45，可看出黏聚力变异系数对震陷最大可靠度影响更为显著。
![]()
图 7 不同参数变异系数对震陷可靠度的影响规律Figure 7. The influence of different parameter coefficient of variations on seismic subsidence reliability4. 结论
（1）Kriging代理模型可以在小样本抽样的情况下得到较好的近似拟合效果，达到精度要求，提高了震陷可靠度的计算效率。
（2）采用震陷可靠度方法来评价地基土体的震陷性，能够合理地考虑土性参数的变异性，更加符合实际情况，具有更好的可靠性和适用性，对于已知地震波峰值加速度，可以快速粗略估计地基震陷的破坏概率，而不是单纯的以震陷量来评价，这在风险评估中具有更为重要的意义。
（3）综合4种土体参数的变异系数对震陷可靠度的影响可以发现，最大可靠度对各个参数的变异系数更为敏感，此外四种土体参数中黏聚力的变异系数对震陷最大可靠度的影响更为显著。
-
![]()
图 6 声发射结合PIV滑移过程分析图
Figure 6. acoustic emission combined with PIV slip process analysis diagrams
表 1 各试验组预测时刻表
Table 1 Predicted timetable for each test group
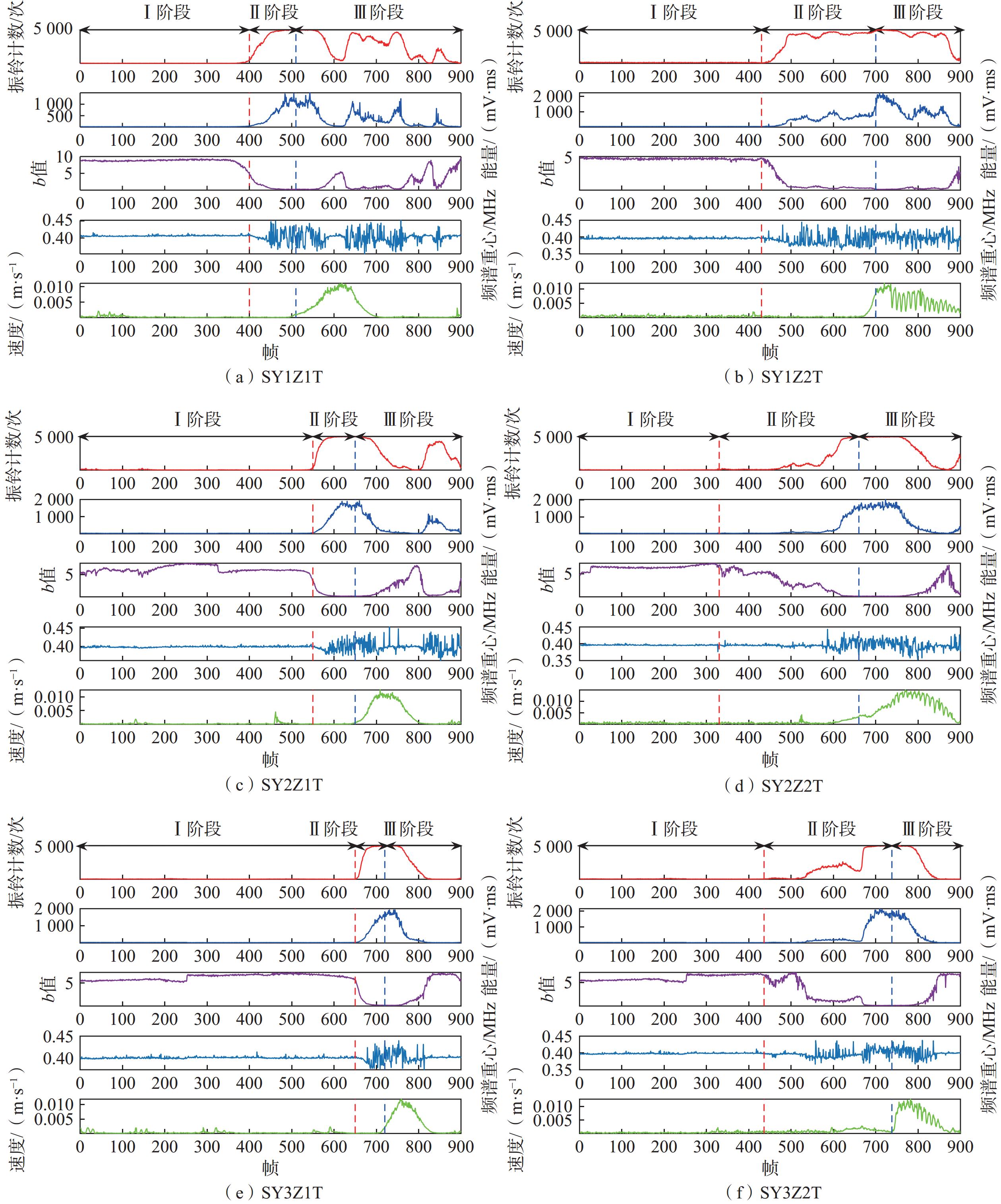
编号 实际滑移点 滑移预警点 提前时间/帧 SY1Z1T 510 439 71 SY1Z2T 700 486 214 SY2Z1T 650 565 85 SY2Z2T 660 586 74 SY3Z1T 720 672 48 SY3Z2T 738 558 180 注：SY1Z1T含义为试验1组第1通道，下同理。 
下载: 导出CSV
-
[1] 邓李政,袁宏永,张鸣之,等. 滑坡变形监测预警技术研究进展[J]. 清华大学学报(自然科学版),2023,63(6):849 − 864. [DENG Lizheng,YUAN Hongyong,ZHANG Mingzhi,et al. Research progress on landslide deformation monitoring and early warning technology[J]. Journal of Tsinghua University (Science and Technology),2023,63(6):849 − 864. (in Chinese with English abstract)] DENG Lizheng, YUAN Hongyong, ZHANG Mingzhi, et al. Research progress on landslide deformation monitoring and early warning technology［J］. Journal of Tsinghua University （Science and Technology）, 2023, 63（6）: 849 − 864. （in Chinese with English abstract）
[2] 冉林,马鹏辉,彭建兵,等. 甘肃黑方台“10•5” 黄土滑坡启动及运动特征分析[J]. 中国地质灾害与防治学报,2022,33(6):1 − 9. [RAN Lin,MA Penghui,PENG Jianbing,et al. The initiation and motion characteristics of the “10•5” loess landslide in the Heifangtai platform,Gansu Province[J]. The Chinese Journal of Geological Hazard and Control,2022,33(6):1 − 9. (in Chinese with English abstract)] RAN Lin, MA Penghui, PENG Jianbing, et al. The initiation and motion characteristics of the “10•5” loess landslide in the Heifangtai platform, Gansu Province［J］. The Chinese Journal of Geological Hazard and Control, 2022, 33（6）: 1 − 9. （in Chinese with English abstract）
[3] 韦忠跟,徐玉龙,丁辉,等. 霍林河北露天煤矿排土场边坡滑坡模式与雷达监测预警[J]. 现代矿业,2022,38(1):71 − 74. [WEI Zhonggen,XU Yulong,DING Hui,et al. Slope landslide mode and radar monitoring and early warning of dump slope in Huolinhe north open-pit coal mine[J]. Modern Mining,2022,38(1):71 − 74. (in Chinese with English abstract)] DOI: 10.3969/j.issn.1674-6082.2022.01.016 WEI Zhonggen, XU Yulong, DING Hui, et al. Slope landslide mode and radar monitoring and early warning of dump slope in Huolinhe north open-pit coal mine［J］. Modern Mining, 2022, 38（1）: 71 − 74. （in Chinese with English abstract） DOI: 10.3969/j.issn.1674-6082.2022.01.016
[4] 丁保艳,翟向华,张卫雄,等. 大型高位堆积体滑坡稳定性分析与数值模拟[J]. 地震工程学报,2022,44(4):786 − 793. [DING Baoyan,ZHAI Xianghua,ZHANG Weixiong,et al. Analysis and numerical simulation of the stability of large high-position accumulation landslides[J]. China Earthquake Engineering Journal,2022,44(4):786 − 793. (in Chinese with English abstract)] DING Baoyan, ZHAI Xianghua, ZHANG Weixiong, et al. Analysis and numerical simulation of the stability of large high-position accumulation landslides［J］. China Earthquake Engineering Journal, 2022, 44（4）: 786 − 793. （in Chinese with English abstract）
[5] 吴绿川,王剑辉,符彦. 基于InSAR技术和光学遥感的贵州省滑坡早期识别与监测[J]. 测绘通报,2021(7):98 − 102. [WU Lyuchuan,WANG Jianhui,FU Yan. Early identifying and monitoring landslides in Guizhou Province with InSAR and optical remote sensing[J]. Bulletin of Surveying and Mapping,2021(7):98 − 102. (in Chinese with English abstract)] WU Lyuchuan, WANG Jianhui, FU Yan. Early identifying and monitoring landslides in Guizhou Province with InSAR and optical remote sensing［J］. Bulletin of Surveying and Mapping, 2021（7）: 98 − 102. （in Chinese with English abstract）
[6] 王琼,欧元超,张平松. 基于文献计量的滑坡监测技术现状及趋势分析[J]. 人民长江,2022,53(8):123 − 132. [WANG Qiong,OU Yuanchao,ZHANG Pingsong. Status and trend analysis of landslide monitoring technology based on bibliometrics[J]. Yangtze River,2022,53(8):123 − 132. (in Chinese with English abstract)] WANG Qiong, OU Yuanchao, ZHANG Pingsong. Status and trend analysis of landslide monitoring technology based on bibliometrics［J］. Yangtze River, 2022, 53（8）: 123 − 132. （in Chinese with English abstract）
[7] 石爱红,李国庆,丁德民,等. 考虑非饱和土基质吸力的丁家坡滑坡变形机制及稳定性评价[J]. 水文地质工程地质,2022,49(6):141 − 151. [SHI Aihong,LI Guoqing,DING Demin,et al. Deformation mechanism and stability evaluation of Dingjiapo landslide considering the matric suction of unsaturated soil[J]. Hydrogeology & Engineering Geology,2022,49(6):141 − 151. (in Chinese with English abstract)] SHI Aihong, LI Guoqing, DING Demin, et al. Deformation mechanism and stability evaluation of Dingjiapo landslide considering the matric suction of unsaturated soil［J］. Hydrogeology & Engineering Geology, 2022, 49（6）: 141 − 151. （in Chinese with English abstract）
[8] BAO Han,LIU Li,LAN Hengxing,et al. Evolution of high-filling loess slope under long-term seasonal fluctuation of groundwater[J]. CATENA,2024,238:107898. DOI: 10.1016/j.catena.2024.107898
[9] CUI Peng,GE Yonggang,LI Shaojun,et al. Scientific challenges in disaster risk reduction for the Sichuan–Tibet Railway[J]. Engineering Geology,2022,309:106837. DOI: 10.1016/j.enggeo.2022.106837
[10] CODEGLIA D,DIXON N,FOWMES G J,et al. Analysis of acoustic emission patterns for monitoring of rock slope deformation mechanisms[J]. Engineering Geology,2017,219:21 − 31. DOI: 10.1016/j.enggeo.2016.11.021
[11] BERG N,SMITH A,RUSSELL S,et al. Correlation of acoustic emissions with patterns of movement in an extremely slow-moving landslide at Peace River,Alberta,Canada[J]. Canadian Geotechnical Journal,2018,55(10):1475 − 1488. DOI: 10.1139/cgj-2016-0668
[12] HU Wei,SCARINGI G,XU Qiang,et al. Acoustic emissions and microseismicity in granular slopes prior to failure and flow-like motion:The potential for early warning[J]. grl,2018,45(19):10.
[13] CHEN Yuzhi,CHEN Shijie. Experimental study on acoustic emission characteristics of bond-slip for BFRP concrete[J]. Russian Journal of Nondestructive Testing,2020,56(2):119 − 130. DOI: 10.1134/S1061830920020035
[14] DENG Lizheng,YUAN Hongyong,CHEN Jianguo,et al. Prefabricated acoustic emission array system for landslide monitoring[J]. Engineering Geology,2023,323:107185. DOI: 10.1016/j.enggeo.2023.107185
[15] 李文彪,王轶,陈新,等. 基于声发射监测的路堤相似模拟破坏过程分形特征研究[J]. 公路,2017,62(7):33 − 38. [LI Wenbiao,WANG Yi,CHEN Xin,et al. Fractal analysis of similar simulation of embankment failure process based on acoustic emission monitoring technology[J]. Highway,2017,62(7):33 − 38. (in Chinese with English abstract)] LI Wenbiao, WANG Yi, CHEN Xin, et al. Fractal analysis of similar simulation of embankment failure process based on acoustic emission monitoring technology［J］. Highway, 2017, 62（7）: 33 − 38. （in Chinese with English abstract）
[16] 胡训健,卞康,刘建,等. 花岗岩晶体粒径分布对声发射特性影响的颗粒流模拟[J]. 煤炭学报,2021,46(增刊2):721 − 730. [HU Xunjian,BIAN Kang,LIU Jian,et al. Particle flow simulation of the influence of granite crystal size distributionon acoustic emission characteristics [J]. Journal of China Coal Society,2021,46(Sup 2):721 − 730. (in Chinese with English abstract)] HU Xunjian, BIAN Kang, LIU Jian, et al. Particle flow simulation of the influence of granite crystal size distributionon acoustic emission characteristics ［J］. Journal of China Coal Society, 2021, 46（Sup 2）: 721 − 730. （in Chinese with English abstract）
[17] 吴鑫,罗筱毓,李龙灿,等. 不同速率下松散颗粒直剪试验声发射特征研究[J/OL]. 西南交通大学学报(2023-09-01)[2023-12-10]. [WU Xin,LUO Xiaoyu,LI Longcan,et al. Experimental research on acoustic emission characteristics of loose particles in direct shear process at different rates[J/OL]. Journal of Southwest Jiaotong University(2023-09-01)[2023-12-10]. https://kns.cnki.net/kcms2/article/abstract?v=Fc1KeZPKhRGwbjFp-Euk0_SSulppLegaQ4PmGickmbI6JAOeM33IXiGUdUHHztT-a6sXD8sFH6yOq769YYfppURcvZGYknmk39NJfwRdMjmms7DbwtOn2uR-m4aW4chDbWE3TEVsXC44u9FtUvxxQy27yuWNKdhxC6sAk4yPOGcuP1S4Yq_8VZgU6m4VSfM2&uniplatform=NZKPT&language=CHS (in Chinese with English abstract)] WU Xin, LUO Xiaoyu, LI Longcan, et al. Experimental research on acoustic emission characteristics of loose particles in direct shear process at different rates［J/OL］. Journal of Southwest Jiaotong University（2023-09-01）[2023-12-10]. https://kns.cnki.net/kcms2/article/abstract?v=Fc1KeZPKhRGwbjFp-Euk0_SSulppLegaQ4PmGickmbI6JAOeM33IXiGUdUHHztT-a6sXD8sFH6yOq769YYfppURcvZGYknmk39NJfwRdMjmms7DbwtOn2uR-m4aW4chDbWE3TEVsXC44u9FtUvxxQy27yuWNKdhxC6sAk4yPOGcuP1S4Yq_8VZgU6m4VSfM2&uniplatform=NZKPT&language=CHS （in Chinese with English abstract）
[18] 陈锡锐,刘虹强,杨剑红,等. 四川宝兴张家沟危岩体稳定性及运动学分析[J]. 中国地质灾害与防治学报,2024,35(2):81 − 89. [CHEN Xirui,LIU Hongqiang,YANG Jianhong,et al. Analysis of stability and kinematics of the dangerous rock mass in Zhangjiagou,Baoxing,Sichuan Province[J]. The Chinese Journal of Geological Hazard and Control,2024,35(2):81 − 89. (in Chinese with English abstract)] CHEN Xirui, LIU Hongqiang, YANG Jianhong, et al. Analysis of stability and kinematics of the dangerous rock mass in Zhangjiagou, Baoxing, Sichuan Province［J］. The Chinese Journal of Geological Hazard and Control, 2024, 35（2）: 81 − 89. （in Chinese with English abstract）
[19] 冯谕,曾怀恩,涂鹏飞. 遗传算法下的滑坡蠕滑位移预测模型研究[J]. 中国地质灾害与防治学报,2024,35(1):82 − 91. [FENG Yu,ZENG Huaien,TU Pengfei. Research on prediction model of landslide creep displacement on genetic algorithm[J]. The Chinese Journal of Geological Hazard and Control,2024,35(1):82 − 91. (in Chinese with English abstract)] FENG Yu, ZENG Huaien, TU Pengfei. Research on prediction model of landslide creep displacement on genetic algorithm［J］. The Chinese Journal of Geological Hazard and Control, 2024, 35（1）: 82 − 91. （in Chinese with English abstract）
[20] HAERI H,SARFARAZI V,SHEMIRANI A B,et al. Field evaluation of soil liquefaction and its confrontation in fine-grained sandy soils (case study:South of Hormozgan Province)[J]. Journal of Mining Science,2017,53(3):457 − 468. DOI: 10.1134/S1062739117032356
[21] 李修磊,谢飞,陈臣,等. 基于声发射的张开型单裂隙岩石裂纹扩展行为特性研究[J]. 水文地质工程地质,2024,51(3):90 − 101. [LI Xiulei,XIE Fei,CHEN Chen,et al. Investigation of crack propagation behavior of opening single fractured rock based on acoustic emission technology[J]. Hydrogeology & Engineering Geology,2024,51(3):90 − 101. (in Chinese with English abstract)] LI Xiulei, XIE Fei, CHEN Chen, et al. Investigation of crack propagation behavior of opening single fractured rock based on acoustic emission technology［J］. Hydrogeology & Engineering Geology, 2024, 51（3）: 90 − 101. （in Chinese with English abstract）
计量
- 文章访问数: 88
- HTML全文浏览量: 6
- PDF下载量: 46
邮件订阅
RSS