Study on warning rainfall threshold for rainfall-induced collapses and landslide geological hazards in Zhuhai City, Guangdong Province
-
摘要:
珠海市雨量充沛，常诱发崩塌、滑坡等突发性地质灾害。文章对珠海市2013—2021年发生的342个崩塌、滑坡地质灾害数据以及特征雨量进行综合分析，总结出珠海市崩塌、滑坡灾害发生与当日降雨量和前4天累计降雨量密切相关，属典型的降雨型崩塌滑坡；通过分析研究灾害发生与降雨的关系，建立了基于有效降雨量阈值的E-D预警模型，并基于2021—2023年珠海市发生的153个崩塌、滑坡地质灾害数据进行预警效果检验，预警准确率为91.5%；以2022年5月12日为例进行单次预警检验，预警命中率为94.7%，漏报率为5.3%，一、二、三级预警区的空报率为16.2%。据此证明建立的E-D预警雨量阈值模型适合珠海实际，可为预警系统的阈值模型改进提供技术依据，也为类似花岗岩地区崩塌、滑坡地质灾害预警技术研究提供借鉴方法。
Abstract:Zhuhai City experiences abundant rainfall, which often triggers sudden geological hazards such as landslides and collapses．This paper conducts a comprehensive analysis of 342 landslide and collapse events that occurred in Zhuhai City between 2013 and 2021, along with their associated rainfall characteristics. The study concludes that the occurrence of landslides and collapses in Zhuhai City is closely related to the daily rainfall and the cumulative rainfall over of the previous four days, classifying these events as typical rainfall-induced collapses and landslides．By analyzing the relationship between hazard occurrence and rainfall, an E-D early warning model based on effective rainfall thresholds was established. The model was tested using 153 collapse and landslide geological disasters from 2021 to 2023 in Zhuhai, resulting in an early warning accuracy of 91.5%．A single early warning test on May 12, 2022, showed a hit rate of 94.7%, a missed report rate of 5.3%, and a false alarm rate of 16.2% for the first, second, and third-level warning zones. The E-D early warning rainfall threshold model established in this study is suitable for the actual conditions in Zhuhai and can provide technical support for improving threshold models in early warning systems. It also offers a reference method for studying early warning techniques for collapse and landslide hazards in similar granite regions．
-
0. 引言
地基稳定性受多种因素影响[1 − 2]，特别是黄土地区，受震陷影响很大。黄土震陷作为一种严重的地质灾害，一旦发生将会造成非常严重的后果。前人对与黄土震陷的研究基本是以动三轴试验为主，以单个震陷量作为震陷性的主要的评价指标[3 − 6]。然而黄土地基震陷的准确性评价受到土性参数不确定性的影响，其中物理力学指标的概率分布类型和变异性会对评价结果产生影响。针对岩土工程中参数、计算模型、荷载等不确定性问题，其主要的不确定性分析方法包括：概率分析方法[7]、随机有限元法[8]、灰色系统评价法[9]、模糊数学法[10]、神经网络评价方法[11]等。这些不确定性方法可以考虑得更加全面，从而提高评价结果的准确性，使结果更为科学合理。
关于黄土震陷在不确定性方面的研究，李波等[12]采用灰色关联方法和逐步判别方法建立了耦合式软土震陷判别模型从而实现软土震陷等级的判定。在黄土震陷概率评价方面，谭芳[13]将概率地震危险性分析方法引入震陷计算中，采用不确定性分析方法分析了黄土震陷与地震参数之间的关系，从而提出一种考虑地震随机性的黄土震陷预测方法。任森等[14]基于大量动三轴试验，结合场地地震危险性概率分析方法，确定了研究区内的震陷区划。孙军杰等[15]依据残余应变估算模型采用概率统计等非确定性分析方法对地基动力沉降进行了概率分析。可见概率分析方法在土体动力沉降中已经得到了初步研究。
然而到目前为止，还没有研究将可靠度理论应用于黄土地基震陷的分析中。因此本文尝试将可靠度理论应用于黄土地基震陷评价中，使用可靠度方法对黄土地基震陷性进行分析。可靠度方法和传统的确定性分析方法相互补充与结合，有助于进行震陷可靠度分析。
1. 黄土地基震陷可靠度指标
可靠度理论在边坡稳定分析中被广泛应用，而边坡工程的不确定因素主要为土体参数的抗剪强度（内摩擦角、黏聚力）[16 − 18]。其依托蒙特卡洛分析法通过计算出多组安全系数值将小于1的安全系数的次数与计算次数的比值称作失效概率。因此可求得对应的可靠度指标（$ \mathrm{\beta } $）为：
$$ \beta ={\varPhi }^{-1}(1-{P}_{\text{f}}) $$ (1) 式中：$ \varPhi $——标准正态分布的累计分布函数；
${P_{\text{f}}}$——失效概率。
在目前已有的地震灾害评估中，尚未有关于地基震陷量的标准划分依据。根据中国地震局发布的《震害调查及地震损失评定工作指南》，可以采用“地基基础破坏等级标准”来评估震陷灾害的程度[16]，将震陷量小于2 cm的定义为基本完好，震陷量大于40 cm的定义为破坏。
参考可靠度理论在边坡稳定性评价中的应用，结合黄土动力学对震陷等级的划分，本文提出了一种对黄土地基震陷评价的可靠度指标。
（1）最大可靠度
在震陷等级划分中将震陷量大于40 cm的定义为震陷破坏，因此可采用破坏概率（Pd）来判定其震陷破坏状态，即$ {P_{\mathrm{d}}} = P\left( {S \geqslant 40} \right) $。将$ \beta_{\mathrm{d}} $定义为：
$$ {\beta _{\mathrm{d}}} = \frac{{40 - {u_{\mathrm{s}}}}}{{{\sigma _{\mathrm{s}}}}} $$ (2) 式中：$ {u_{\mathrm{s}}} $——震陷量的平均值；
$ {\sigma _{\mathrm{s}}} $——震陷量的标准差。
如果震陷量符合标准正态分布，破坏概率与可靠度的关系可表示为：
$$ {P_{\mathrm{d}}} = P\left( {S > 40} \right) = 1 - \varPhi \left(\frac{{40 - {u_{\mathrm{s}}}}}{{{\sigma _{\mathrm{s}}}}}\right) = 1 - \varPhi ({\beta _{\mathrm{d}}}) $$ (3) 则根据可靠度理论，将破坏概率对应的可靠度称为最大可靠度（${\beta }_{\text{d}} $），也就是指衡量地基震陷最大安全程度的标准，其计算公式为：
$$ {\beta }_{\text{d}}={\varPhi }^{-1}(1-{P}_{\text{d}}) $$ (4) 根据蒙特卡罗可靠度计算方法可定义破坏概率为：
$$ {P_{\text{d}}} = \frac{M}{N} $$ (5) 式中：$ {P}_{{\mathrm{d}}} $——地基震陷破坏概率；
M——抽样次数中震陷量大于40 cm的次数；
N——蒙特卡洛分析法总的抽样次数。
（2）最小可靠度
在震陷等级划分中将震陷量小于2 cm的定义为基本完好，因此可采用完好概率（Ph）来判定其完好状态，即$ {P_{\mathrm{h}}} = P\left( {S \leqslant 2} \right) $。将$ {\beta _{\mathrm{h}}} $定义为：
$$ {\beta _{\mathrm{h}}} = \frac{{2 - {u_{\mathrm{s}}}}}{{{\sigma _{\mathrm{s}}}}} $$ (6) 式中：$ {u_{\mathrm{s}}} $——震陷量的平均值；
$ {\sigma _{\mathrm{s}}} $——震陷量的标准差。
如果震陷量符合标准正态分布，完好概率（Ph）与可靠度的关系可表示为：
$$ {P_{\mathrm{h}}} = P\left( {S < 2} \right) = \varPhi \left(\frac{{2 - {u_{\mathrm{s}}}}}{{{\sigma _{\mathrm{s}}}}}\right) = \varPhi ({\beta _{\mathrm{h}}}) $$ (7) 根据可靠度理论，将完好概率对应的可靠度称为最小可靠度（${\beta _{\mathrm{h}}} $），也就是指衡量地基震陷完好程度的标准，其计算公式为：
$$ {\beta _{\text{h}}} = {\varPhi ^{ - 1}}\left( {{P_{\text{h}}}} \right) $$ (8) 根据蒙特卡罗可靠度计算方法可定义完好概率为：
$$ {P_{\text{h}}} = \frac{M}{N} $$ (9) 式中：$ {P}_{{\mathrm{h}}} $——地基完好概率；
M——抽样次数中震陷量小于2 cm的次数；
N——蒙特卡洛分析法总的抽样次数。
2. 基于Kriging代理模型的震陷可靠度计算
2.1 Kriging代理模型的建立
Kriging模型是一种基于方差最小的无偏估计方法，它的原理是通过已知样本点的线性加权法来预测未知点的函数值，即已知加权系数插值就可求得变量空间内任一点的函数值。Kriging代理模型通常情况下由回归部分和随机误差两部分所组成。将其用输出变量S(x)与输入变量x表示为：
$$ S({\boldsymbol{x}}) = \sum\limits_{i = 1}^m {{\beta _i}} f({\boldsymbol{x}}) + {\textit{z}}({\boldsymbol{x}}) = f{({\boldsymbol{x}})^T}{\boldsymbol{\beta}} + {\textit{z}}({\boldsymbol{x}}) $$ (10) 式中：每个样本点中输入变量的个数为n，$ {\boldsymbol{x}} = [ {x_1},{x_2}, \cdots , {x_n} ]^T$，$ f(x) = {\left[ {{f_1}(x),{f_2}(x), \cdots ,{f_m}(x)} \right]^T} $为回归多项式基函数向量，m为回归多项式的数量；${\boldsymbol{\beta}} = {[{\beta _1},{\beta _2},\cdots,{\beta _m}]^T}$为多项式参数向量，z(x)为一均值为0，方差为$ {\sigma ^2} $的正态随机过程，该随机过程的协方差为：
$$ COV\left[{\textit{z}}(u),{\textit{z}}(v)\right]={\sigma }^{2}R({u,v}) $$ (11) 其中，R表示任意两点u，v的相关函数，通常取为高斯相关方程，即：
$$ R(u,v) = \exp \left\{ { - \theta {{(u - v)}^2}} \right\} $$ (12) 其中，$ \theta $为相关参数，可通过最大似然估计得到：
$$ \theta=\max \left\{ { - \left[ {\frac{1}{2}\ln \left( {\left| R \right|} \right)} \right] + \frac{k}{2}\ln \left( {{\sigma ^2}} \right)} \right\} $$ (13) 其中，R为相关矩阵，元素R=R(u,v)。
基于给定的样本点，多项式参数向量$\beta $与随机过程方差$ {\sigma ^2} $的估计值分别为：
$$ \left\{ {\begin{split} & {\hat {\boldsymbol{\beta}} = {{\left( {{{\boldsymbol{F}}^T}{{\boldsymbol{R}}^{ - 1}}{\boldsymbol{F}}} \right)}^{ - 1}}{{\boldsymbol{F}}^T}{{\boldsymbol{R}}^{ - 1}}{\boldsymbol{Y}}} \\ & {{{\hat {\boldsymbol{\sigma}} }^2} = \frac{1}{k}{{\left( {{\boldsymbol{Y}} - {\boldsymbol{F}}\hat {\boldsymbol{\beta}} } \right)}^T}{{\boldsymbol{R}}^{ - 1}}\left( {{\boldsymbol{Y}} -{\boldsymbol{ F}}\hat {\boldsymbol{\beta}} } \right)} \end{split}} \right. $$ (14) 其中，F为由回归多项式函数值构成的矩阵。
对于任意输入变量$ {x_0} $,假定$ {x_0} $与输入变量样本X之间的相关系数向量为$ {{\boldsymbol{r}}_0} = {\left[ {R\left( {{x_0},{x_1}} \right), \cdots ,R\left( {{x_0},{x_k}} \right)} \right]^T} $利用式（10）构建的Kriging模型表达式，可以得到与$ {x_0} $对应的系统响应值$ S({x_0}) $的预测值$ \hat S({x_0}) $服从正态分布$ N(\hat S({x_0}),{\hat \sigma _{\hat S}}^2({x_0})) $,$ S({x_0}) $的最佳线性无偏估计及均方误差可表示为：
$$ \left\{ {\begin{split} &{\hat S\left( {{x_0}} \right) = {f^T}({x_0})\hat {\boldsymbol{\beta}} + {{\boldsymbol{r}}_0}^T{{\boldsymbol{R}}^{ - 1}}({\boldsymbol{Y}} - {\boldsymbol{F}}\hat {\boldsymbol{\beta }})} \\ & {{{\hat \sigma }^2}_{\hat S}({x_0}) = {{\hat \sigma }^2}\left( {1 + {{\boldsymbol{u}}^T}{{({{\boldsymbol{F}}^T}{{\boldsymbol{R}}^{ - 1}}{\boldsymbol{F}})}^{ - 1}}{\boldsymbol{u}} - {{\boldsymbol{r}}_0}^T{{\boldsymbol{R}}^{ - 1}}{{\boldsymbol{r}}_0}} \right)} \end{split}} \right. $$ (15) 其中，$ {{{\boldsymbol{u}} = }}{{{{\boldsymbol{F}}}}^T}{{\boldsymbol{R}}^{ - 1}}{{\boldsymbol{r}}_0} - {\boldsymbol{f}} $。
本文进行震陷可靠度分析时，式（10）—（15）中应用Kriging模型构建和预测其过程，采用MATLAB中的DACE工具箱实现。
2.2 黄土地基数值模型
采用FLAC3D有限差分软件建立黄土地基数值模型，模型尺寸设置为15 m×15 m×15 m，模型网格数为
3375 ，本构模型选择Mohr-Coulomb弹塑性本构模型。在静力分析时，底面和侧面选用固定边界，限制底面与侧面的位移和速度，顶部为自由边界。动力分析与静力分析不同，由于地震荷载会存在波的反射，因此在模型底面设置静态边界，侧面设置为自由场边界，模拟土体在实际中的状态（图1）。本文选用三条地震波分别是Kobe地震波、Imperial地震波和一条人工合成波。为方便后续说明，这里将选用的三条地震波分别命名为地震波1、地震波2及地震波3。地震波1的持续时间为25 s，时间间隔为0.02 s，最大加速度为0.345g，地震波2的持续时间为40 s，时间间隔为0.01 s，最大加速度为0.313g，地震波3的持续时间为20 s，时间间隔为0.02 s，最大加速度为0.153g。图2为经过滤波以及基线校正后所选地震波的时程曲线。
为了研究不同地震水平作用下震陷变形规律，将其改变幅值的大小来满足不同工况的需要，得到 0.1g、0.2g、0.3g、0.4g、0.5g、0.6g、0.7g不同峰值加速度大小的7种水平。其计算所得震陷量结果如表1所示。
表 1 不同地震波及不同峰值加速度作用下地基震陷量Table 1. Seismic subsidence of foundation under different seismic waves and peak accelerations.峰值加速度/g 震陷量/cm 地震波1 地震波2 地震波3 0.1 0.72 1.95 2.65 0.2 2.37 8.40 13.44 0.3 9.10 16.02 21.62 0.4 17.83 21.44 29.52 0.5 19.78 25.29 37.06 0.6 20.08 30.67 40.98 0.7 20.48 35.84 46.98 2.3 震陷变形影响因素敏感性分析
岩土体材料参数存在着变异性，但土体泊松比的变异系数非常小，在考虑土性参数不确定时可将其看作常量。孙军杰等[17]通过理论分析，给出了非饱和黄土动残余应变与黏聚力、内摩擦角、初始孔隙比、土层重度、土层埋深以及地震动荷载之间的定量关系式。压缩模量是体现土体压缩性的指标之一，作为土体的力学性质，在分析地基土体变形或沉降时起着重要作用，而土体的黏聚力和内摩擦角反映土体的强度特征，在静力分析中，黄土地基静力参数中密度对于计算结果的影响较明显。因此，这里选择密度、弹性模量、黏聚力及内摩擦角四种参数。采用FLAC3D结合灰色关联分析对影响黄土地基震陷变形的因素做敏感性分析，求得其密度、弹性模量、黏聚力及摩擦角四个参数的灰色关联度为$ q = [ {0.656\;8},\;{0.856\;2},\;{0.668\;5},\;{0.728\;1} ] $，敏感性排序为：弹性模量>内摩擦角>黏聚力>密度。
2.4 土性参数分布概率模型
本节选取密度（ρ）、压缩模量（Es）、黏聚力（c）及内摩擦角（φ）四种参数作为黄土震陷性评价的参数指标来进行分布概率模型研究。为了全面分析不同地貌单元4种土性参数的最优概率分布，选用可以包含大部分不确定性因素的概率分布形式包括正态分布、对数正态分布和威布尔分布进行假设检验。从而确定每个参数的最优概率分布形式[18]。
为获取原状黄土地基土性不同参数的分布概率模型，基于引汉济渭工程的渭河二级阶地地貌土体为例，通过对原状黄土的各种物理力学指标进行统计分析，得出各指标服从的概率密度函数及分布参数，图3所示为渭河二级阶地分布概率模型图，其中$ f\left( x \right) $表示概率密度函数。
![]()
图 3 不同参数的概率密度分布图Figure 3. Probability density distribution plots of different parameters由图3可知，从分布形态上来看，$ \rho $值的正态分布和对数正态分布整体较一致，两者均属于左偏态；其余三种土性参数正态分布、对数正态分布及威布尔分布三者分布较离散，差异性较大。
通过K-S检验法对4种土性参数的3种分布概率模型进行检验，求出样本值的理论累计概率分布与经验累计概率分布的最大差值（Dmax），与由显著性水平和样本数确定临界值（$ D_n^\alpha $）进行比较，计算结果如表2所示。四种参数均可接受正态分布、对数正态分布和威布尔分布。$ c $、$ {E_{\mathrm{s}}} $值的最优分布是正态分布，$ \varphi $、$ \rho $值的最优分布是威布尔分布，考虑到正态分布的优良性质，将正态分布作为4种土性参数的分布概率模型用于震陷可靠度计算。
表 2 分布假设检验结果Table 2. Distribution hypothesis test results检验参数 样本量 验证结果$ {D_{\max }} $ 可接受的临界值
$ D_n^\alpha /\left( {\alpha = 0.05} \right) $正态分布 对数正态分布 威布尔分布 结果 $ {D_{\max }} $ 结果 $ {D_{\max }} $ 结果 $ {D_{\max }} $ 内摩擦角 24 √ 0.180 √ 0.223 √ 0.093 0.273 黏聚力 24 √ 0.099 √ 0.125 √ 0.102 0.273 压缩模量 24 √ 0.094 √ 0.146 √ 0.164 0.273 密度 48 √ 0.150 √ 0.185 √ 0.115 0.196 2.5 基于Kriging代理模型的震陷可靠度计算方法
本节基于Kriging代理模型对地基震陷可靠度进行计算，这里进行
10000 次模拟，计算步骤如下：（1）根据前文统计出的土性参数（密度、压缩模量、黏聚力、摩擦角）的概率分布模型，确定地基土体参数的均值、标准差、分布类型等统计特性。
（2）FLAC3D6.0内置有Python编程语言，可以实现蒙特卡洛抽样与连续计算，利用Itasca开发的专门用于Python扩展编程的程序库，通过编程实现随机变量拉丁超立方抽样（LHS）、模型的建立以及计算，即会产生N组计算方案$ \left(\rho_1,E_{\mathrm{s}1},c_1,\varphi_1\right),\left(\rho_2,E_{\mathrm{s}2},c_2,\varphi_2\right),\cdots,(\rho_n,E_{\mathrm{s}n},c_n, \varphi_n) $，然后计算出对应的响应值。将计算模型文件保存为“n.f3sav”，后续模型按顺序编号，并将其作为源文件以便后续提取。
（3）对地震波设计不同的工况组合，计算每组工况下LHS的样本所对应的震陷量，并保存计算模型。
（4）利用Python编程语言从结果文件中批量提取竖向变形。
（5）采用MATLAB软件分别建立不同工况下的Kriging代理模型，以4种土体参数为输入，相应的地基震陷量为输出，对代理模型进行训练，得到满足精度要求的代理模型。经适当训练的代理模型能够较好地逼近实际情况，在此基础上可以十分方便地预测震陷值从而实现震陷可靠度的计算（图4）。
![]()
图 4 基于Kriging代理模型的震陷可靠度计算流程Figure 4. Calculation process of seismic subsidence reliability based on the Kriging surrogate model3. 算例分析
为验证本文提出方法的适用性，本节以引汉济渭工程为背景结合Kriging代理模型的震陷概率计算方法开展黄土地基震陷可靠度分析。
（1）最大可靠度
表3为不同地震波及不同地震峰值加速度作用下地基震陷的破坏概率，以渭河二级阶地为例。
表 3 不同地震波作用下地基震陷破坏概率Table 3. Probability of foundation subsidence failure under different seismic wave effects加速度/g 地震波1 地震波2 地震波3 0.1 0 0 0 0.2 0 0 0 0.3 0 0 0 0.4 0 0.072 0.116 0.5 0 0.17 0.378 0.6 0 0.232 0.704 0.7 0.002 0.264 0.888 由表3可知，在地震波1的作用下，该地基土体在地震波峰值加速度为0.7g时会出现破坏的概率，在地震波2和地震波3的作用下，在峰值加速度达到0.4g时会出现破坏的概率。三条地震波在峰值加速度达到最大时，其产生的破坏概率也有巨大差异，地震波1在峰值加速度为0.7g时破坏概率为0.002，地震波2在峰值加速度为0.7g时破坏概率为0.264，地震波3在峰值加速度为0.7g时破坏概率为0.888。
依据式（4）求得最大可靠度指标，图5为不同地震波作用下地基震陷的可靠度指标随峰值加速度的变化规律，最大可靠度指标的范围为−1.216～4.526。总体上可靠度指标随峰值加速度的增加呈非线性减小。但三条地震波的减小斜率并不相同，在地震波3作用下，可靠度指标随峰值加速度的变化斜率最大，说明在地震波3作用下，地基的可靠度受地震波峰值加速度的影响最大。对于已知地震波峰值加速度，可以快速粗略估计地基震陷的破坏概率，而不是单纯以震陷量来评价，这在风险评估中具有更为重要的意义。
![]()
图 5 可靠度分析获得的地基震陷最大可靠度Figure 5. Maximum reliability index of foundation seismic subsidence obtained from reliability analysis（2）最小可靠度
表4为不同地震波及不同地震峰值加速度作用下地基震陷的破坏概率，以渭河二级阶地为例。由表4可知，在地震波1的作用下，该地基土体在地震波峰值加速度为0.1g～0.7g时均会出现完好概率，在地震波2和地震波3的作用下，在峰值加速度分别达到0.4g及以后和0.3g及以后完好概率均为0。
表 4 不同地震波作用下地基震陷完好概率Table 4. Probability of intact seismic subsidence of foundation under different seismic wave effects加速度/g 地震波1 地震波2 地震波3 0.1 0.946 0.854 0.842 0.2 0.392 0.094 0.832 0.3 0.238 0.004 0 0.4 0.01 0 0 0.5 0.018 0 0 0.6 0.012 0 0 0.7 0.002 0 0 依据式（8）求得最小可靠度指标，图6为在不同地震波作用下地基震陷的最小可靠度随峰值加速度的变化规律，最小可靠度指标的变化范围为−2.878～1.607。从整体来说，随着地震峰值加速度的增大，地基在地震作用下的最小可靠度指标逐渐降低。当地震峰值加速度为0.1g时，震陷最小可靠度较高，都为正值；当地震峰值加速度为0.2g时，地震最小可靠度显著减小，且超过0.2g以后最小可靠度均为负值。
![]()
图 6 可靠度分析获得的地基震陷的最小可靠度指标Figure 6. Minimum reliability index of foundation seismic subsidence obtained from reliability analysis（3）变异系数对震陷可靠度的影响
为了更好地分析随机变量的变异性大小对震陷可靠度的影响，本文计算了各变量在不同变异系数组合情况下，四种土体参数变异系数随地基震陷可靠度的变化情况，工况组合见表5。
表 5 各参数变异系数工况组合表Table 5. Combination table of variation coefficient for each parameter工况 COV 密度 弹性模量 黏聚力 摩擦角 1-1 0.01 0.3 0.2 0.3 1-2 0.05 1-3 0.1 1-4 0.15 1-5 0.2 2-1 0.05 0.05 0.2 0.3 2-2 0.1 2-3 0.2 2-4 0.3 2-5 0.4 3-1 0.05 0.3 0.05 0.3 3-2 0.1 3-3 0.2 3-4 0.3 3-5 0.4 4-1 0.05 0.3 0.2 0.1 4-2 0.2 4-3 0.3 4-4 0.4 4-5 0.5 计算结果如图7所示。由图可知，随各参数变异系数的增加，震陷最大可靠度逐渐减小，而最小可靠度逐渐增大。当$ COV(\rho) $从0.01增加至0.2，相应的$ {\beta _{\text{d}}} $从3.72减小至3.05，最小可靠度（$ {\beta _{\text{h}}} $）从−1.72增加至−1.55，降幅为21.97%，增幅为10.96%；当$ COV(E_{\mathrm{s}}) $从0.05增加至0.4，相应的$ {\beta _{\text{d}}} $从3.89降至3.29，$ {\beta _{\text{h}}} $从−1.89增加至−1.64，降幅为18.24%，增幅为15.24%；当$ COV(c) $从0.05增加至0.4，$ {\beta _{\text{d}}} $从4.26降至2.89，$ {\beta _{\text{h}}} $从−1.81增加至−1.60，降幅为47.40%，增幅为13.13%；当$ COV(\varphi)$从0.1增加至0.5，$ {\beta _{\text{d}}} $从3.72降至2.74，$ {\beta _{\text{h}}} $从−1.99增加至−1.63，降幅为35.77%，增幅为22.09%。对比数据，在同样的增幅下，最大可靠度的变化幅度比最小可靠度的变化幅度大说明最大可靠度对变异系数更为敏感。计算各个参数最大可靠度起末两点斜率的绝对值，分别为3.526、1.714、3.914和2.45，可看出黏聚力变异系数对震陷最大可靠度影响更为显著。
![]()
图 7 不同参数变异系数对震陷可靠度的影响规律Figure 7. The influence of different parameter coefficient of variations on seismic subsidence reliability4. 结论
（1）Kriging代理模型可以在小样本抽样的情况下得到较好的近似拟合效果，达到精度要求，提高了震陷可靠度的计算效率。
（2）采用震陷可靠度方法来评价地基土体的震陷性，能够合理地考虑土性参数的变异性，更加符合实际情况，具有更好的可靠性和适用性，对于已知地震波峰值加速度，可以快速粗略估计地基震陷的破坏概率，而不是单纯的以震陷量来评价，这在风险评估中具有更为重要的意义。
（3）综合4种土体参数的变异系数对震陷可靠度的影响可以发现，最大可靠度对各个参数的变异系数更为敏感，此外四种土体参数中黏聚力的变异系数对震陷最大可靠度的影响更为显著。
-
![]()
图 1 珠海市崩塌、滑坡地质灾害分布图（2013—2021年）
Figure 1. Distribution map of landslides and collapse geological hazards in Zhuhai City (2013—2021)
![]()
图 2 珠海市崩塌、滑坡地质灾害特征图
Figure 2. Characteristic map of landslides and collapse geological hazards in Zhuhai City
![]()
图 4 地质灾害事件与有效降雨量、降雨历时散点图
Figure 4. Scatter diagram of geological hazard events, effective rainfall, and rainfall duration
![]()
图 6 2022年5月12日预警信息发布和地质灾害分布图
Figure 6. Distribution map of geological hazards and early warning information issed on May 12，2022
表 1 崩塌、滑坡灾害数量与月均降雨量关系表
Table 1 Relationship between the number of collapses and landslide hazards and average monthly rainfall
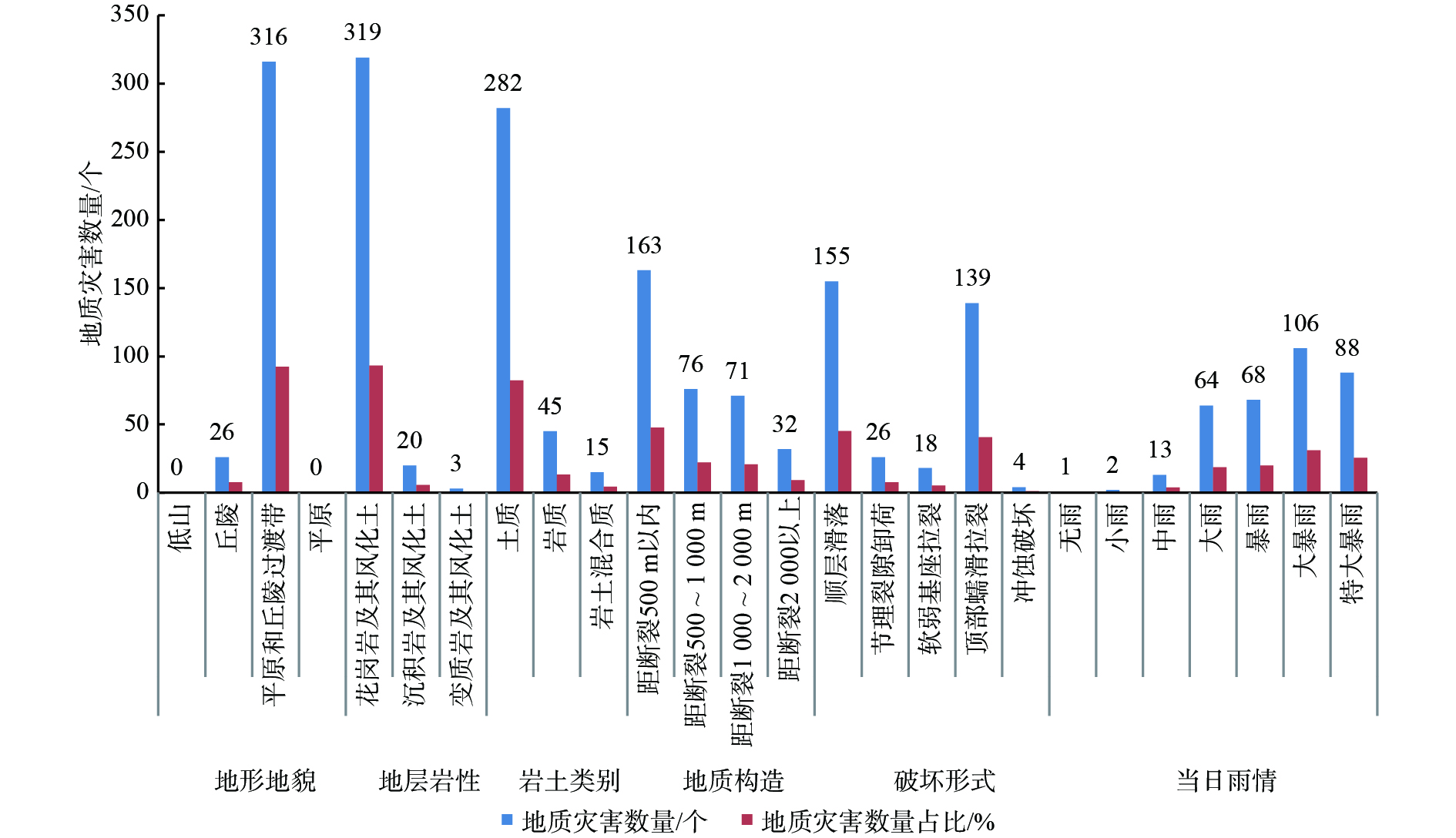
月份 1 2 3 4 5 6 7 8 9 10 11 12 平均降雨量/mm 26.9 57.9 84.7 199.6 298.1 390.0 319.3 336.7 220.8 71.7 44.3 30.6 地质灾害数量/个 1 0 5 15 162 56 14 61 24 3 1 0 
下载: 导出CSV
表 2 地质灾害数量与当日降雨量关系表
Table 2 Relationship between the number of geological hazards and daily rainfall
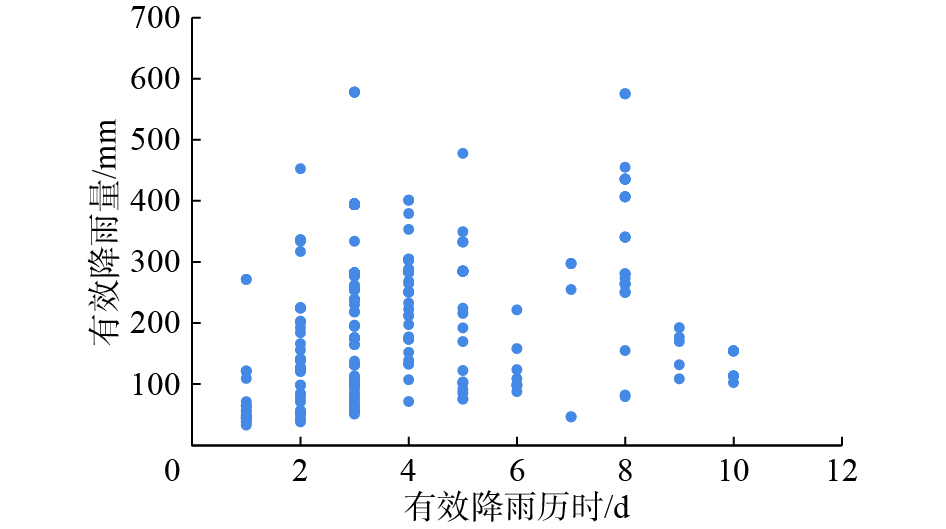
当日降雨量/mm 0 0.1～9.9 10.0～24.9 25.0～49.9 50.0～99.9 100.0～249.9 ≥250 降雨量等级 无雨 小雨 中雨 大雨 暴雨 大暴雨 特大暴雨 地质灾害数量/个 1 2 13 64 68 106 88 灾害数量占比/% 0.3 0.6 3.8 18.7 19.9 31.0 25.7
下载: 导出CSV
表 3 崩塌、滑坡灾害数量与前4天累计降雨量关系
Table 3 Relationship between the number of collapse and landslide hazards and cumulative rainfall over the previous four days
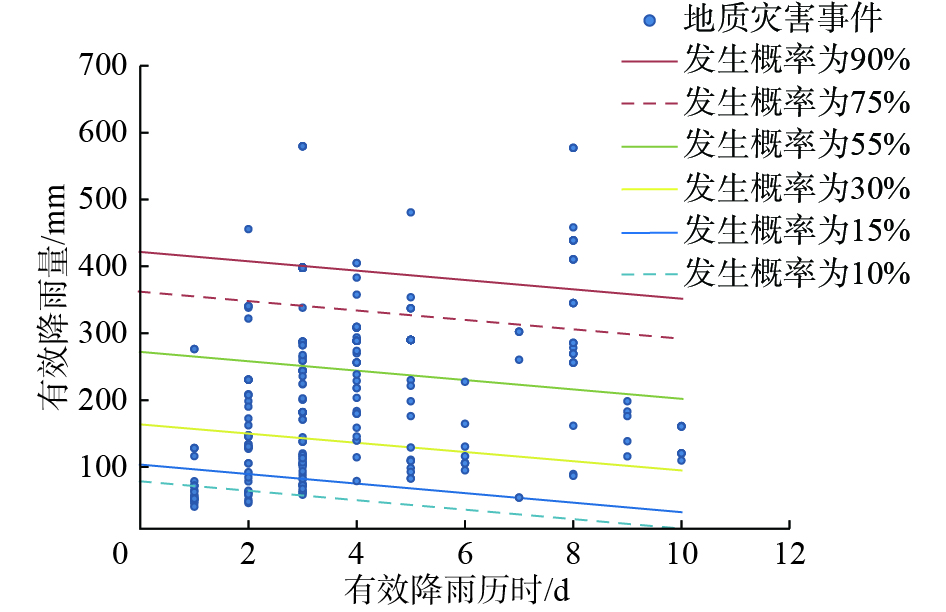
前4天累计降雨量/mm 0～50 50～100 100～150 150～200 200～250 250～300 300～350 ≥350 地质灾害数量/个 8 27 18 3 2 4 16 2 灾害数量占比/% 10.0 33.7 22.5 3.8 2.5 5.0 20.0 2.5
下载: 导出CSV
表 4 不同概率的有效降雨量阈值
Table 4 Effective rainfall thresholds for different probabilities
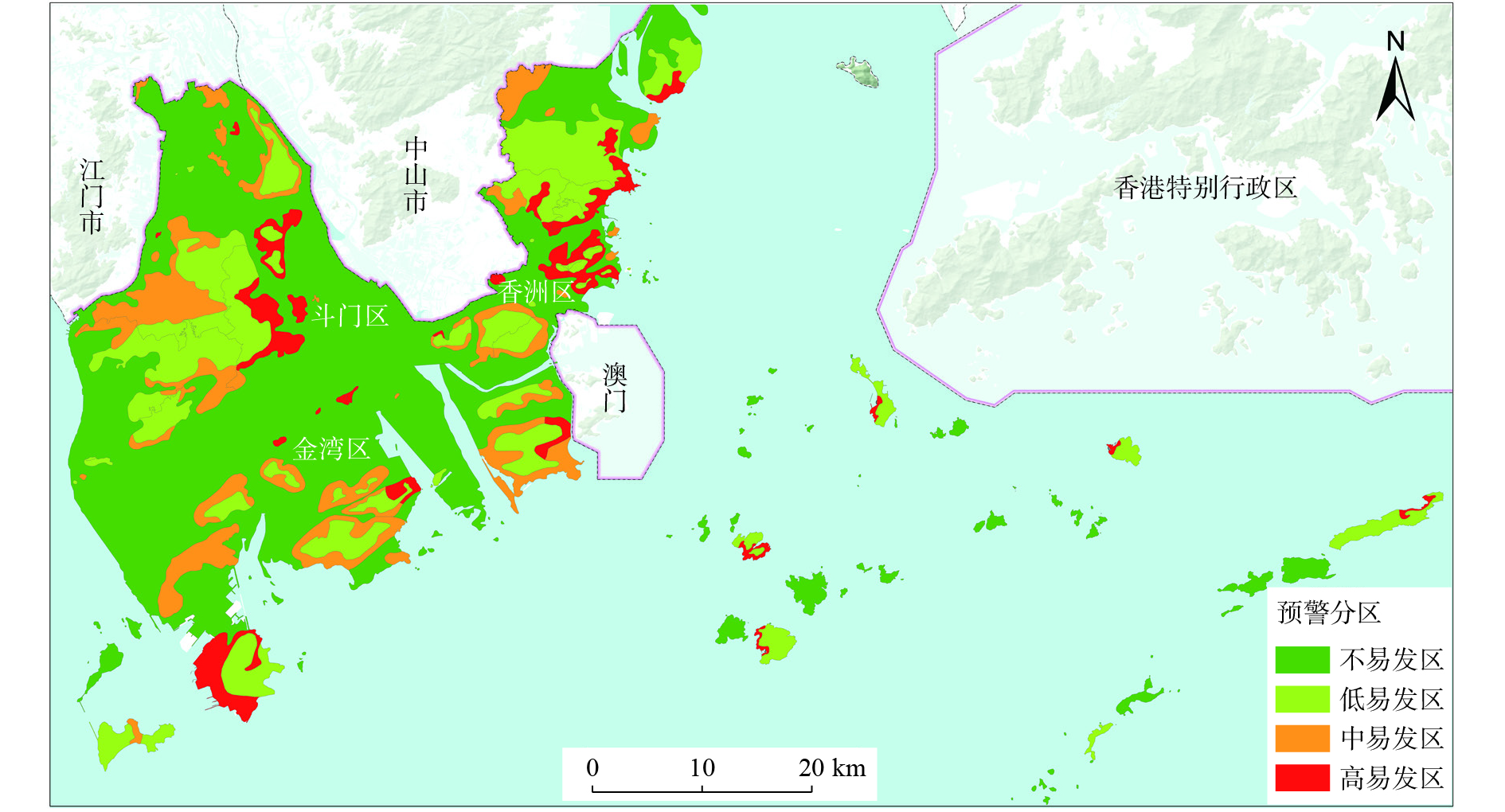
发生概率/% 10 15 30 55 75 90 阈值模型 E =59.37D−0.185 E =81.51D−0.185 E= 147.95D−0.185 E=258.67D−0.185 E= 347.25D−0.185 E=413.65D−0.185 有效降雨量阈值/mm 59.37 81.51 147.95 258.67 347.25 413.65
下载: 导出CSV
表 5 不同易发程度分区各预警等级的有效降雨量阈值
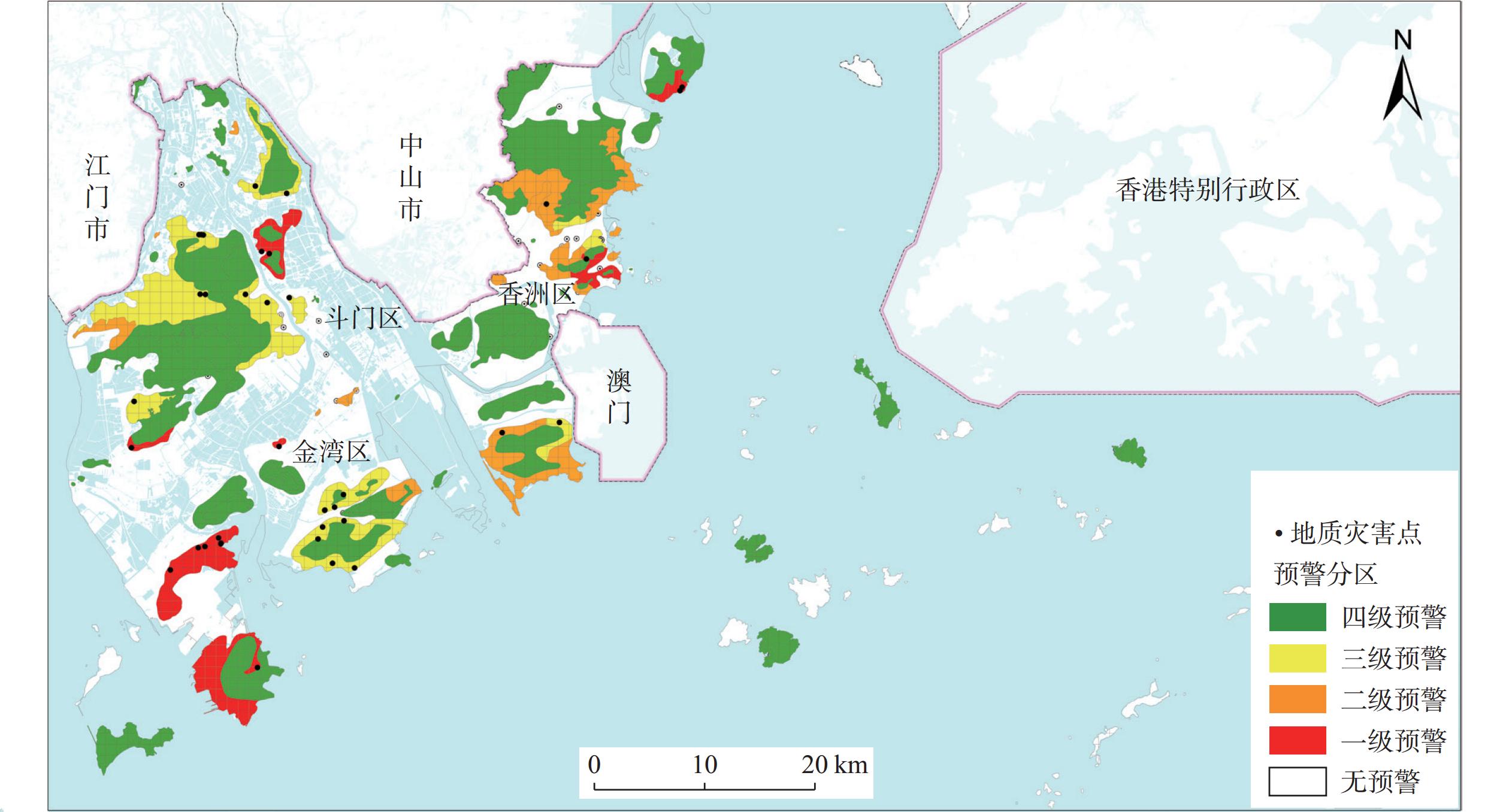
Table 5 Effective rainfall thresholds for different early warning levels in various susceptibility zones
/mm 易发程度 预警级别 四级预警 三级预警 二级预警 一级预警 高易发区 59.37 147.95 258.67 347.25 中易发区 59.37 258.67 347.25 413.65 低易发区 81.51 347.25 413.65 —
下载: 导出CSV
表 6 地质灾害预警准确率计算表
Table 6 Accuracy calculation table for geological hazard early warnings
预警等级 无预警 落入四级预警区 落入三级预警区 落入二级预警区 落入一级预警区 合计 高易发区 地灾点数量/个 8 13 25 12 16 74 占比/% 10.8 17.6 33.8 16.2 21.6 100 中易发区 地灾点数量/个 5 22 8 21 10 66 占比/% 7.6 33.3 12.1 31.8 15.2 100 低易发区 地灾点数量/个 0 10 2 1 0 13 占比/% 0 76.9 15.4 7.7 0 100 合计 地灾点数量/个 13 45 35 34 26 153 占比/% 8.5 29.4 22.9 22.2 17.0 100
下载: 导出CSV
表 7 2022年5月12日暴雨引发地质灾害预警准确率
Table 7 Accuracy of geological hazard Early warning triggered by rainstorm on May 12，2022
预警等级 预警区外 落入四级预警区 落入三级预警区 落入二级预警区 落入一级预警区 合计 地灾点数量/个 2.0 0 2.00 22.00 12.00 38.00 占比/% 5.3 0 5.30 57.90 31.50 100.00 发布预警区面积/km2 — 418.86 73.94 112.97 64.70 670.47 有灾点的预警区面积/km2 — 0 37.20 108.92 64.70 210.82
下载: 导出CSV
表 8 2022年5月12日暴雨引发地质灾害命中率
Table 8 Hit rate of geological hazards triggered by rainstorm on May 12， 2022
预警等级 四级预警区 三级预警区 二级预警区 一级预警区 合计 网格单元数量/个 418 74 113 65 670 有地灾点的网格单元数量/个 0 2 22 12 36 占比（命中率）/% 0 2.7 19.5 18.5 5.4 无地灾点的网格单元数量/个 418 72 91 53 634 占比（空报率）/% 0 97.3 80.5 81.5 94.6
下载: 导出CSV
-
[1] REX L,Baum . 美国降雨诱发的浅层滑坡和泥石流预警[J]. 水文地质工程地质技术方法动态,2011(5):45 − 58. [REX,L,BAUM,et al. Early warning of shallow landslides and mudslides induced by rainfall in the United States[J]. Information of Hydrogeology & Engineering Geology Techniques,2011(5):45 − 58. (in Chinese with English abstract)] REX, L, BAUM, et al. Early warning of shallow landslides and mudslides induced by rainfall in the United States［J］. Information of Hydrogeology & Engineering Geology Techniques, 2011（5）: 45 − 58. （in Chinese with English abstract）
[2] 梁润娥,李中社,苗高建,等. 区域地质灾害气象预警模型研究现状与展望[J]. 安全与环境工程,2013,20(1):30 − 35. [LIANG Rune,LI Zhongshe,MIAO Gaojian,et al. Current situation and prospect of regional geo-hazards meteorological early warning model[J]. Safety and Environmental Engineering,2013,20(1):30 − 35. (in Chinese with English abstract)] DOI: 10.3969/j.issn.1671-1556.2013.01.07t LIANG Rune, LI Zhongshe, MIAO Gaojian, et al. Current situation and prospect of regional geo-hazards meteorological early warning model［J］. Safety and Environmental Engineering, 2013, 20（1）: 30 − 35. （in Chinese with English abstract） DOI: 10.3969/j.issn.1671-1556.2013.01.07t
[3] 刘艳辉,刘传正,温铭生,等. 中国地质灾害气象预警模型研究[J]. 工程地质学报,2015,23(4):738 − 746. [LIU Yanhui,LIU Chuanzheng,WEN Mingsheng,et al. Study of early warning models for regional geo-hazards in China[J]. Journal of Engineering Geology,2015,23(4):738 − 746. (in Chinese with English abstract)] LIU Yanhui, LIU Chuanzheng, WEN Mingsheng, et al. Study of early warning models for regional geo-hazards in China［J］. Journal of Engineering Geology, 2015, 23（4）: 738 − 746. （in Chinese with English abstract）
[4] 肖锐铧,刘艳辉,陈春利,等. 中国地质灾害气象风险预警20年:2003—2022[J]. 中国地质灾害与防治学报,2024,35(2):1 − 9. [XIAO Ruihua,LIU Yanhui,CHEN Chunli,et al. 20-year early warning for regional geo-hazards risk in China:2003-2022[J]. The Chinese Journal of Geological Hazard and Control,2024,35(2):1 − 9. (in Chinese with English abstract)] XIAO Ruihua, LIU Yanhui, CHEN Chunli, et al. 20-year early warning for regional geo-hazards risk in China: 2003-2022［J］. The Chinese Journal of Geological Hazard and Control, 2024, 35（2）: 1 − 9. （in Chinese with English abstract）
[5] 周剑,汤明高,许强,等. 重庆市滑坡降雨阈值预警模型[J]. 山地学报,2022,40(6):847 − 858. [ZHOU Jian,TANG Minggao,XU Qiang,et al. Early warning model of rainfall-induced landslide in Chongqing of China based on rainfall threshold[J]. Mountain Research,2022,40(6):847 − 858. (in Chinese with English abstract)] DOI: 10.3969/j.issn.1008-2786.2022.6.sdxb202206006 ZHOU Jian, TANG Minggao, XU Qiang, et al. Early warning model of rainfall-induced landslide in Chongqing of China based on rainfall threshold［J］. Mountain Research, 2022, 40（6）: 847 − 858. （in Chinese with English abstract） DOI: 10.3969/j.issn.1008-2786.2022.6.sdxb202206006
[6] 谢剑明,刘礼领,殷坤龙,等. 浙江省滑坡灾害预警预报的降雨阀值研究[J]. 地质科技情报,2003,22(4):101 − 105. [XIE Jianming,LIU Liling,YIN Kunlong,et al. Study on the threshold valves of rainfall of landslide hazards for early-warning and prediction in Zhejiang Province[J]. Geological Science and Technology Information,2003,22(4):101 − 105. (in Chinese with English abstract)] XIE Jianming, LIU Liling, YIN Kunlong, et al. Study on the threshold valves of rainfall of landslide hazards for early-warning and prediction in Zhejiang Province［J］. Geological Science and Technology Information, 2003, 22（4）: 101 − 105. （in Chinese with English abstract）
[7] 陈伟,许强. 地质灾害降雨预警基准研究[J]. 地球与环境,2011,39(3):393 − 398. [CHEN Wei,XU Qiang. Study on the benchmark of rainfall as early warning for geohazards[J]. Earth and Environment,2011,39(3):393 − 398. (in Chinese with English abstract)] CHEN Wei, XU Qiang. Study on the benchmark of rainfall as early warning for geohazards［J］. Earth and Environment, 2011, 39（3）: 393 − 398. （in Chinese with English abstract）
[8] 宋昭富,张勇,佘涛,等. 基于易发性分区的区域滑坡降雨预警阈值确定——以云南龙陵县为例[J]. 中国地质灾害与防治学报,2023,34(4):22 − 29. [SONG Zhaofu,ZHANG Yong,SHE Tao,et al. Determination of regional landslide rainfall warning threshold based on susceptibility zoning:A case study in Longling County of Yunnan Province[J]. The Chinese Journal of Geological Hazard and Control,2023,34(4):22 − 29. (in Chinese with English abstract)] SONG Zhaofu, ZHANG Yong, SHE Tao, et al. Determination of regional landslide rainfall warning threshold based on susceptibility zoning: A case study in Longling County of Yunnan Province［J］. The Chinese Journal of Geological Hazard and Control, 2023, 34（4）: 22 − 29. （in Chinese with English abstract）
[9] 陈海龙,宋晓玲,张永军,等. 甘肃省白龙江流域不同岩性滑坡降雨阈值研究[J]. 中国地质灾害与防治学报,2024,35(2):40 − 46. [CHEN Hailong,SONG Xiaoling,ZHANG Yongjun,et al. Study on rainfall threshold of different lithologic landslides in Bailong River Basin of Gansu Province[J]. The Chinese Journal of Geological Hazard and Control,2024,35(2):40 − 46. (in Chinese with English abstract)] CHEN Hailong, SONG Xiaoling, ZHANG Yongjun, et al. Study on rainfall threshold of different lithologic landslides in Bailong River Basin of Gansu Province［J］. The Chinese Journal of Geological Hazard and Control, 2024, 35（2）: 40 − 46. （in Chinese with English abstract）
[10] 刘艳辉,唐灿,李铁锋,等. 地质灾害与降雨雨型的关系研究[J]. 工程地质学报,2009,17(5):656 − 661. [LIU Yanhui,TANG Can,LI Tiefeng,et al. Statistical relations between geo-hazards and rain-type[J]. Journal of Engineering Geology,2009,17(5):656 − 661. (in Chinese with English abstract)] DOI: 10.3969/j.issn.1004-9665.2009.05.012 LIU Yanhui, TANG Can, LI Tiefeng, et al. Statistical relations between geo-hazards and rain-type［J］. Journal of Engineering Geology, 2009, 17（5）: 656 − 661. （in Chinese with English abstract） DOI: 10.3969/j.issn.1004-9665.2009.05.012
[11] 珠海市1∶5万地质灾害详细调查报告[R]. 珠海:广东省珠海工程勘察院,2020. [Detailed survey report on 1∶50,000 geological hazards in Zhuhai City[R]. Zhuhai:Guangdong Zhuhai Engineering Exploration Institute,2020. (in Chinese)] Detailed survey report on 1∶50, 000 geological hazards in Zhuhai City［R］. Zhuhai: Guangdong Zhuhai Engineering Exploration Institute, 2020. （in Chinese）
[12] 广东省珠海市1∶10万地质灾害风险调查报告[R]. 珠海:广东省珠海工程勘察院,2022. [Risk investigation report on 1∶10 0000 geological hazards in Zhuhai of Guangdong Province[R]. Zhuhai:Guangdong Zhuhai Engineering Exploration Institute,2022. (in Chinese)] Risk investigation report on 1∶10 0000 geological hazards in Zhuhai of Guangdong Province［R］. Zhuhai: Guangdong Zhuhai Engineering Exploration Institute, 2022. （in Chinese）
[13] 魏平新,郑志文,周志华,等. 广东省暴雨型浅层滑坡灾害动力预警模型与气象风险预警研究[J]. 中国地质灾害与防治学报,2024,35(2):30 − 39. [WEI Pingxin,ZHENG Zhiwen,ZHOU Zhihua,et al. Research on risk early warning for rainfall-induced shallow landslides in Guangdong Province based on a dynamic slope instability model[J]. The Chinese Journal of Geological Hazard and Control,2024,35(2):30 − 39. (in Chinese with English abstract)] WEI Pingxin, ZHENG Zhiwen, ZHOU Zhihua, et al. Research on risk early warning for rainfall-induced shallow landslides in Guangdong Province based on a dynamic slope instability model［J］. The Chinese Journal of Geological Hazard and Control, 2024, 35（2）: 30 − 39. （in Chinese with English abstract）
[14] 林春泽,王宁涛,王清,等. 降雨型滑坡地质灾害预警预报研究进展[J]. 暴雨灾害,2018,37(5):393 − 400. [LIN Chunze,WANG Ningtao,WANG Qing,et al. Research progress in early warning and forecast of rainfall-typed landslide geological hazards[J]. Torrential Rain and Disasters,2018,37(5):393 − 400. (in Chinese with English abstract)] DOI: 10.3969/j.issn.1004-9045.2018.05.001 LIN Chunze, WANG Ningtao, WANG Qing, et al. Research progress in early warning and forecast of rainfall-typed landslide geological hazards［J］. Torrential Rain and Disasters, 2018, 37（5）: 393 − 400. （in Chinese with English abstract） DOI: 10.3969/j.issn.1004-9045.2018.05.001
[15] CROZIER M J,EYLES R J. Assessing the probability of rapid massmovement[C]//Anon. Proceeding third Australia-New Zealand Conference on Geomechanics. Wellington:New Zealand Institution of Engineers-Proceedings of Technical Groups,1980.
[16] 周诗凯,刘正华,余丰华,等. 浙江省地质灾害气象风险预警一体化建设的探索与实践[J]. 中国地质灾害与防治学报,2024,35(2):21 − 29. [ZHOU Shikai,LIU Zhenghua,YU Fenghua,et al. Exploration and practice of integrated construction of meteorological risk warning for geological hazards in Zhejiang Province[J]. The Chinese Journal of Geological Hazard and Control,2024,35(2):21 − 29. (in Chinese with English abstract)] ZHOU Shikai, LIU Zhenghua, YU Fenghua, et al. Exploration and practice of integrated construction of meteorological risk warning for geological hazards in Zhejiang Province［J］. The Chinese Journal of Geological Hazard and Control, 2024, 35（2）: 21 − 29. （in Chinese with English abstract）
[17] 杨寅,林建,包红军. 2018年地质灾害重点区域气象预警效果检验[J]. 中国地质灾害与防治学报,2019,30(6):135 − 140. [YANG Yin,LIN Jian,BAO Hongjun. Evaluation of meteorological early warning to major regions affected by geological hazards in 2018[J]. The Chinese Journal of Geological Hazard and Control,2019,30(6):135 − 140. (in Chinese with English abstract)] YANG Yin, LIN Jian, BAO Hongjun. Evaluation of meteorological early warning to major regions affected by geological hazards in 2018［J］. The Chinese Journal of Geological Hazard and Control, 2019, 30（6）: 135 − 140. （in Chinese with English abstract）
[18] 刘艳辉,温铭生,苏永超,等. 台风暴雨型地质灾害时空特征及预警效果分析[J]. 水文地质工程地质,2016,43(5):119 − 126. [LIU Yanhui,WEN Mingsheng,SU Yongchao,et al. Characteristics of geo-hazards induced by typhoon rainstorm and evaluation of geo-hazards early warning[J]. Hydrogeology & Engineering Geology,2016,43(5):119 − 126. (in Chinese with English abstract)] LIU Yanhui, WEN Mingsheng, SU Yongchao, et al. Characteristics of geo-hazards induced by typhoon rainstorm and evaluation of geo-hazards early warning［J］. Hydrogeology & Engineering Geology, 2016, 43（5）: 119 − 126. （in Chinese with English abstract）
[19] 王惠卿, 肖锐铧, 刘艳辉, 等. 近20年地质灾害气象风险预警研究文献图谱可视化分析[J]. 中国地质灾害与防治学报,2024,35(2):10 − 20. [WANG Huiqing, XIAO Ruihua, LIU Yanhui, et al. Visualization analysis of research literature on early warning of geo-hazards based on meteorological factors in the past 20 years[J]. The Chinese Journal of Geological Hazard and Control,2024,35(2):10 − 20. (in Chinese with English abstract)] WANG Huiqing, XIAO Ruihua, LIU Yanhui, et al. Visualization analysis of research literature on early warning of geo-hazards based on meteorological factors in the past 20 years［J］. The Chinese Journal of Geological Hazard and Control, 2024, 35（2）: 10 − 20. （in Chinese with English abstract）
计量
- 文章访问数: 178
- HTML全文浏览量: 21
- PDF下载量: 105
邮件订阅
RSS