Analysis on factors controlling shallow failures of the cut slopes and its prevention by bio-engineering measures: A case study of the cut slopes along the highway from Shuangcheng to Dajiali
-
摘要:
有效掌握边坡浅层塌滑机制及其影响因素的主次关系是开展路堑边坡变形预测及塌滑治理的重要前提。为此,以阵雨条件下甘肃省双达高速某路堑边坡为研究对象,首先通过FLAC3D有限元软件平台编写FISH语言,实现饱和度、重度和土体抗剪强度之间的动态关联,然后求解不同降雨强度、坡比和降雨历时条件下路堑边坡的安全系数,并基于灰色关联理论确定路堑边坡浅层塌滑主要外界因素的主次关系,最后通过室内降雨试验和现场生态防护试验总结出路堑边坡浅层塌滑机制,提出浅层塌滑生态防治措施。研究表明:降雨过程中,路堑边坡破坏模式由深层整体滑动向浅层局部滑动演化,且随坡比的降低,浅层塌滑区域由路堑边坡的坡肩部位向坡脚部位演化;相比降雨强度和降雨历时,坡比对路堑边坡浅层塌滑影响性最大;降雨过程中,路堑边坡浅层土体累计冲蚀率随时间呈现出先降低后增加的趋势,设置拱骨架和降低坡比均能提高路堑边坡浅层土体的抗塌滑能力;相比HP-FGM和EFM防护材料,聚丙烯纤维土防护材料时效性最理想,路堑边坡浅层塌滑生态治理效果最好。
Abstract:Understanding the primary and secondary relations of influencing factors is crucial for predicting deformation and controlling collapse in cutting slopes. Using a cutting slope along the Shuangcheng to Dalijia expressway in Gansu Province as the research object, this research utilized the FLAC3D finite element software platform to establish dynamic correlations between saturation, gravity, and soil shear strength through FISH language. Based on this, safety factors of the cutting slope were calculated under different rainfall intensities, slope ratios, and rainfall duration. Grey relational theory was applied to determine the primary and secondary relationships of key factors affecting shallow collapse of cutting slopes under rainfall conditions. Indoor rainfall experiments and on-site ecological protection tests were conducted to summarize the shallow collapse mechanism and propose the environmental control measures. The study revealed that the failure mode of cutting slopes transitioned from deep overall sliding to shallow local sliding during rainfall. As the slope ratio decreased, the shallow collapse area gradually shifted from the slope shoulder to the foot of the cutting slope. Cumulative erosion rates of shallow soil in cutting slopes decreased initially and then increased over time during rainfall. Installing arch skeletons and reducing the slope ratio enhanced the cutting slope's resistance against shallow collapses. Among with the protective materials, polypropylene fiber-reinforced soil protective materials exhibited the best timeliness and ecological control effect for shallow collapses of cutting slopes compared to HP-FGM and EFM materials.
-
Keywords:
- cutting slope /
- safety factor /
- grey correlation theory /
- numerical simulation /
- shallow collapse
-
0. 引 言
随着我国经济发展战略向西部倾斜,西部地区交通基础建设工程数量正逐年递增,工程建设虽然给西部地区提供了新的发展机遇,但也因此产生了大量的土质路堑边坡,在降雨作用下路堑边坡频发滑塌灾害,严重影响公路的生态建设及安全运营。
降雨条件下,路堑边坡塌滑灾害已成为制约山区公路建设的重要问题之一。目前,相关学者[1]认为一般情况下降雨诱发的为浅层斜坡破坏;李同录等[2]认为边坡浅层滑移是降雨坡面直接入渗引起,且浅层滑移的厚度相当于湿润锋的深度,一般不超过2 m;石诚鋆等[3]通过数值模拟分析了降雨条件下坡比、坡高、雨强、降雨历时以及土体渗透系数等因素对边坡稳定性的影响;蔡荣坤等[4]依托实际工程案例,重点分析降雨强度、降雨历时及边坡坡率对边坡潜在滑动模式的影响;孙萍萍等[5]基于Hydrus中的Slope Cube模块,通过数值模拟手段分析了不同坡型的黄土边坡在降雨条件下的浅层破坏过程以及破坏机制;胡华等[6]通过模拟室内降雨滑坡试验,比较了不同坡度和降雨强度条件下的斜坡滑塌破坏机理;杜忠原等[7]和李宁等[8]分别通过数值模拟研究了降雨条件下锚杆和抗滑桩支护作用对边坡稳定性的影响,并分析了不同支护条件下边坡浅层的破坏形态。但关于降雨条件下路堑边坡浅层塌滑机制及其影响因素的主次关系研究不够深入。
本文依托甘肃省双达高速公路K28段路堑边坡,首先通过FLAC3D有限元软件平台的二次开发技术编写FISH语言,实现饱和度、重度和土体抗剪强度之间的动态关联,然后基于强度折减法分析不同变量下(降雨强度、降雨历时和坡比)路堑边坡的安全系数和破坏形式,并根据灰色关联理论分析各变量对边坡稳定性影响程度的主次关系,最后分别通过室内降雨试验和现场生态防护试验总结出路堑边坡浅层塌滑机制,提出浅层塌滑的生态防治措施,研究成果对降雨条件下路堑边坡浅层塌滑灾害防治具有参考价值。
1. 灰色关联度理论
灰色关联分析法是通过比较自变量和因变量数据序列曲线的几何形状相似度,并据此判断两者之间的关联性[9],其具体步骤如下:
(1)原始数据无量纲和归一化
将边坡安全系数的影响因素作为自变量参考矩阵X,将边坡的安全系数作为因变量参考矩阵Y,矩阵 X和矩阵 Y相似,其中矩阵X为:
$$ {{{\boldsymbol{X}}}} = \left[ {\begin{array}{*{20}{c}} {{{{X}}_1}} \\ {{{{X}}_2}} \\ \vdots \\ {{{{X}}_m}} \end{array}} \right] = {\left[ {\begin{array}{*{20}{c}} {{{{x}}_{11}}}&{{{{x}}_{12}}}& \cdots &{{{{x}}_{1n}}} \\ {{x_{21}}}&{{x_{22}}}& \cdots &{{{{x}}_{2n}}} \\ \vdots & \vdots & \ddots & \vdots \\ {{{{x}}_{m1}}}&{{{{x}}_{m2}}}& \cdots &{{{{x}}_{mn}}} \end{array}} \right]^{{{m}} \times {{n}}}} $$ (1) 通过无量纲和归一化参考矩阵X可得:
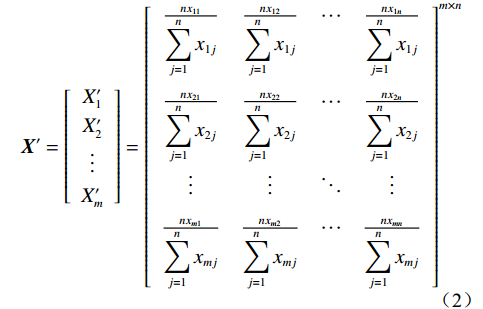
$$ {{{\boldsymbol{X}}'}} = \left[ {\begin{array}{*{20}{c}} {{X'_1}} \\ {{X'_2}} \\ \vdots \\ {{X'_m}} \end{array}} \right] = {\left[ {\begin{array}{*{20}{c}} {\frac{{{{n}}{{{x}}_{11}}}}{{\displaystyle\sum\limits_{{{j}} = 1}^{{n}} {{{{x}}_{1j}}} }}}&{\frac{{{{n}}{{{x}}_{12}}}}{{\displaystyle\sum\limits_{{{j}} = 1}^{{n}} {{{{x}}_{1j}}} }}}& \cdots &{\frac{{{{n}}{{{x}}_{1n}}}}{{\displaystyle\sum\limits_{{{j}} = 1}^{{n}} {{{{x}}_{1j}}} }}} \\ {\frac{{{{n}}{{{x}}_{21}}}}{{\displaystyle\sum\limits_{{{j}} = 1}^{{n}} {{{{x}}_{2j}}} }}}&{\frac{{{{n}}{{{x}}_{22}}}}{{\displaystyle\sum\limits_{{{j}} = 1}^{{n}} {{{{x}}_{2j}}} }}}& \cdots &{\frac{{{{n}}{{{x}}_{2n}}}}{{\displaystyle\sum\limits_{{{j}} = 1}^{{n}} {{{{x}}_{2j}}} }}} \\ \vdots & \vdots & \ddots & \vdots \\ {\frac{{{{n}}{{{x}}_{m1}}}}{{\displaystyle\sum\limits_{{{j}} = 1}^{{n}} {{{{x}}_{mj}}} }}}&{\frac{{{{n}}{{{x}}_{m2}}}}{{\displaystyle\sum\limits_{{{j}} = 1}^{{n}} {{{{x}}_{mj}}} }}}& \cdots &{\frac{{{{n}}{{{x}}_{mn}}}}{{\displaystyle\sum\limits_{{{j}} = 1}^{{n}} {{{{x}}_{mj}}} }}} \end{array}} \right]^{{{m}} \times {{n}}}} $$ (2) 同理,可计算出无量纲和归一化后因变量参考矩阵
$ {{{\boldsymbol{Y}}'}} $ 。(2)关联系数计算
对归一化后的自变量参考矩阵
${{\boldsymbol{X}}'_{{{mn}}}}$ 和因变量参考矩阵${{\boldsymbol{Y}}'_{{{mn}}}}$ 进行差异性分析,其差异性矩阵为:$$ {\Delta }_{{mn}}={\left[\left|X '_{1}-Y '_{1}\right|{,}\left|X '_{2}-Y '_{2}\right|{,}\cdots {,}\left|X '_{{m}}-Y '_{{m}}\right|\right]}^{{{T}}} $$ (3) 由式(3)可得到差异性矩阵元素的最大值和最小值分别为:
$$ {{M}} = {\text{max}}({\Delta _{{{mn}}}}) $$ (4) $$ {{m}} = {\text{min}}({\Delta _{{{mn}}}}) $$ (5) 自变量和因变量对应元素间的关联系数为:
$$ \xi ({\Delta _{{{mn}}}}) = \frac{{{{m}} + \rho \cdot {{M}}}}{{{\Delta _{{{mn}}}} + \rho \cdot {{M}}}} $$ (6) 式中:ξ(∆mn) ——关联系数矩阵,这里ξ(∆mn)其实是差 异序列矩阵∆mn的灰色关联系数矩阵;
M、m——差异序列矩阵元素的最大值和最小值;
ρ——分辨系数,
$ \rho \in [0,1] $ ,一般取0.5。(3)灰色关联度计算
根据式(6)将各因素的关联系数均值作为该因素评价指标的关联度ri:
$$ {{{r}}_{{m}}} = \frac{1}{{{n}}}\sum\limits_{{\rm{j}} = 1}^{\rm{n}} \xi ({\Delta _{{{mn}}}})$$ (7) 式中:n——计算对象数量。
根据式(7)可求出各因素关联度,按照从大到小的顺序进行排列,ri值越大,自变量和因变量间的关联度越高,即自变量对因变量的影响最大。
2. 有限元计算案例
2.1 工程背景
双达高速某路堑边坡位于甘肃省临夏县、夏河县与青海省循化县交界处K28+655—K28+800段,坡体高度为6.72 m,坡度为1∶1,采用拱形骨架植草护坡,坡体上部为碎石土,以粉质黏土为主,颜色呈灰褐色,密实程度为稍密或中密,室内测得天然含水率平均值为23.52%,其中碎石含量约为20%,粒径为20~60 mm,层厚3.6 m;中部为全风化闪长岩,构造基本风化破坏,岩芯破碎,多呈泥柱状,含少量碎块状,层厚5.5 m;下部为强风化闪长岩,块状构造,矿物成分以辉石、角闪石等为主,节理裂隙较发育,岩芯破碎,多呈碎块状,少量短柱状,层厚10.3 m,其现场全貌见图1。
2.2 计算模型参数
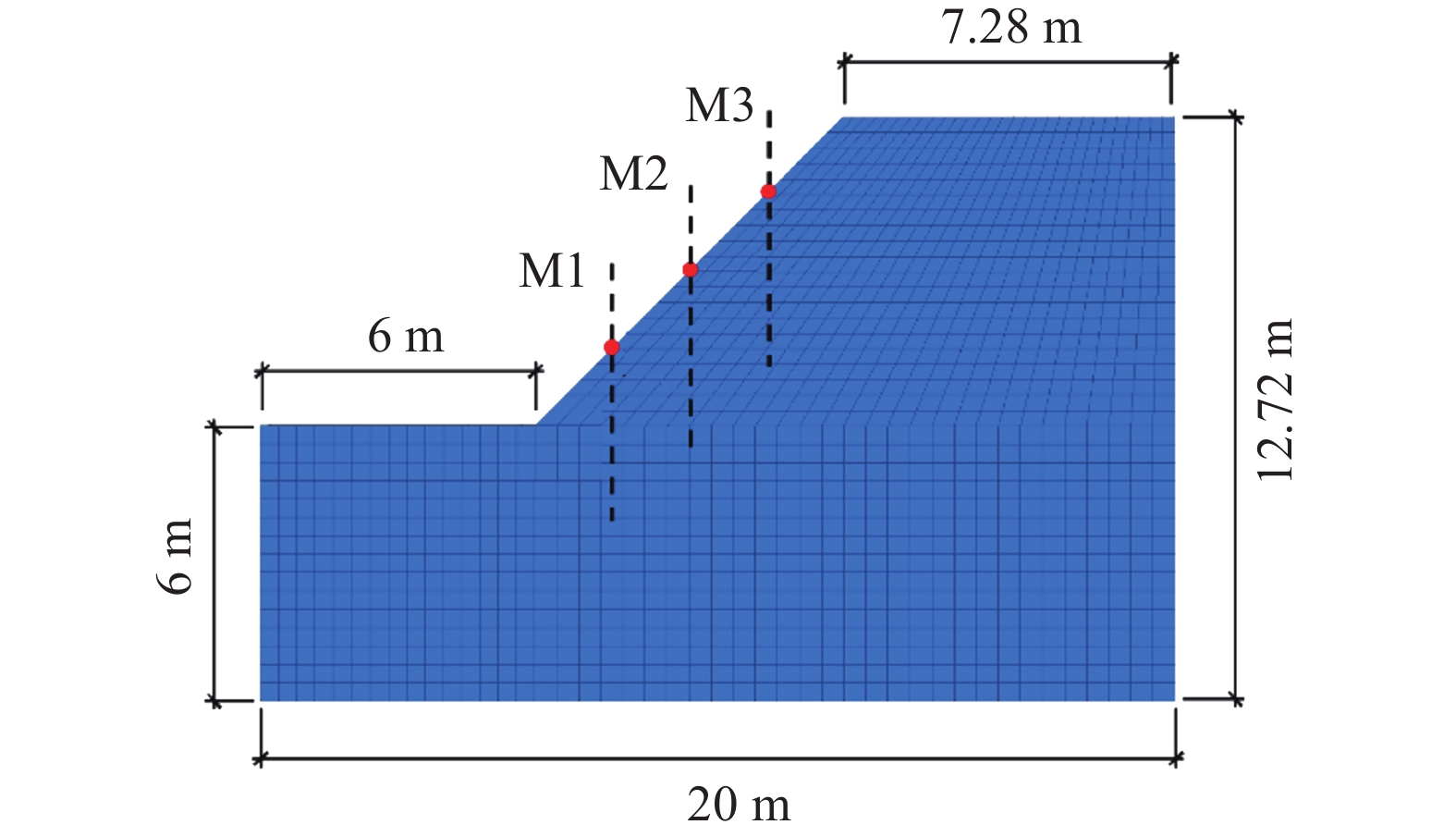
根据现场情况设置坡体高度为6.72 m,坡比为1∶1,降雨强度为5 mm/h,降雨历时为48 h,地表基质吸力为50 kPa,基质吸力沿深度呈线性分布。降雨过程中,若降雨强度小于或等于坡体最外侧土体入渗率时,入渗率取降雨强度,反之则取土体最大渗透系数。模型侧面及底面固定,侧面设置为不透水边界,模型底部设置为透水边界,选用各向同性渗流模型,土体本构为Mohr-Coulomb模型。设置M1、M2和M3剖面分别监测坡脚、坡中和坡肩部位的孔隙水压力变化,模型尺寸及网格划分如图2所示,相关参数见表1。
表 1 土体材料参数Table 1. Basic physical parameters of undisturbed soil弹性模量
/MPa泊松比 密度
/(g·cm−3)渗透系数
/(cm·s−1)有效黏聚力
/kPa有效内摩擦
角/(°)12.00 0.3 1.88 4.5×10-5 26.7 28.5 2.3 土-水特征曲线
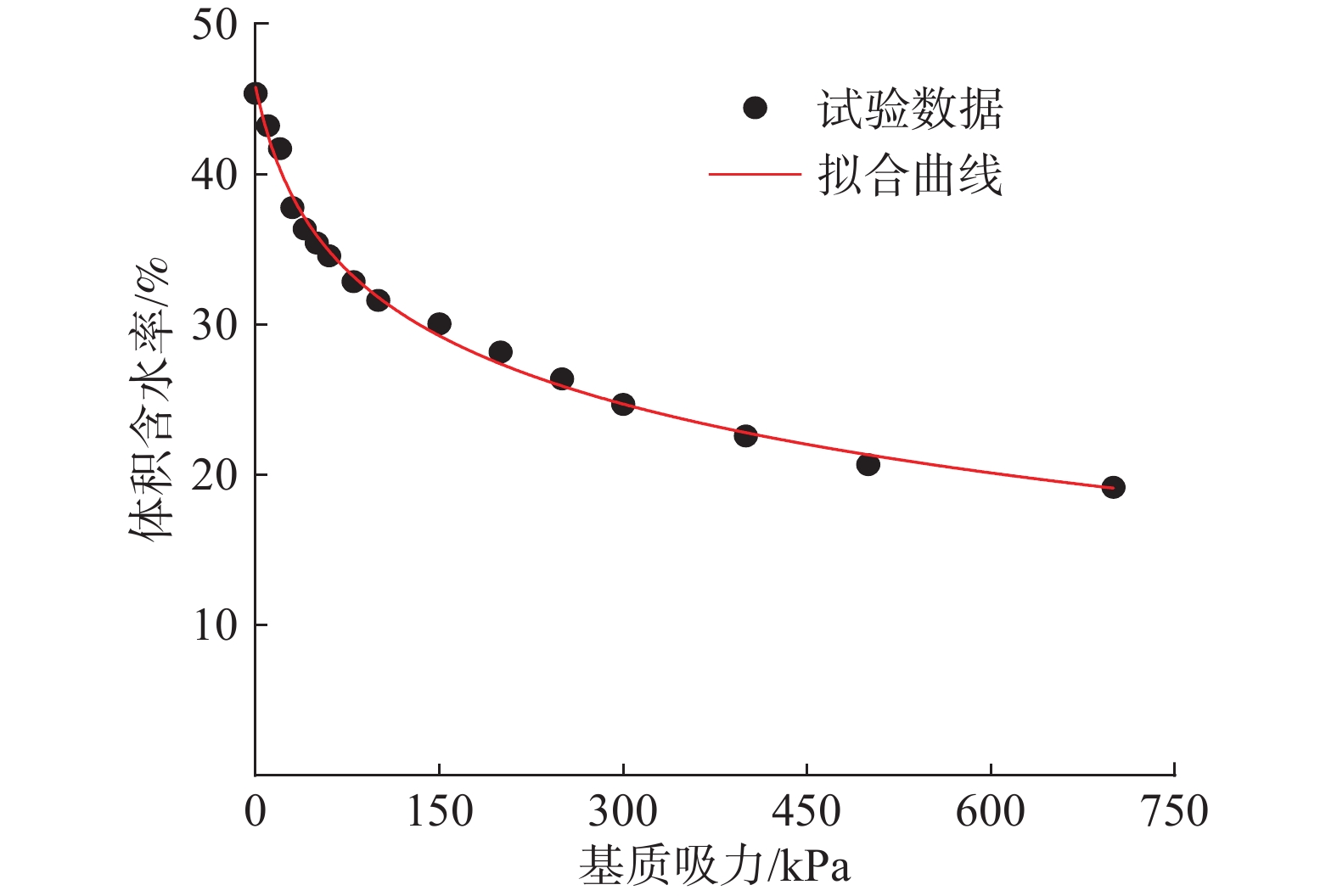
通过压力膜仪获取不同含水率对应的基质吸力(图3试验数据),然后结合Van-Genuchten数学模型[10]得到体积含水率和基质吸力之间的关系,拟合出相应的土水特征曲线(图3拟合曲线),并计算出相应的VG模型参数(表2),其中θs为饱和体积含水率, θr为残余体积含水率,α、n为拟合参数 ,R2为拟合度。
表 2 VG模型参数Table 2. Summary table of VG model parameters参数 θs θr α n R2 取值 0.4592 0.0837 0.0720 1.2661 0.9655 2.4 非饱和土体抗剪强度参数
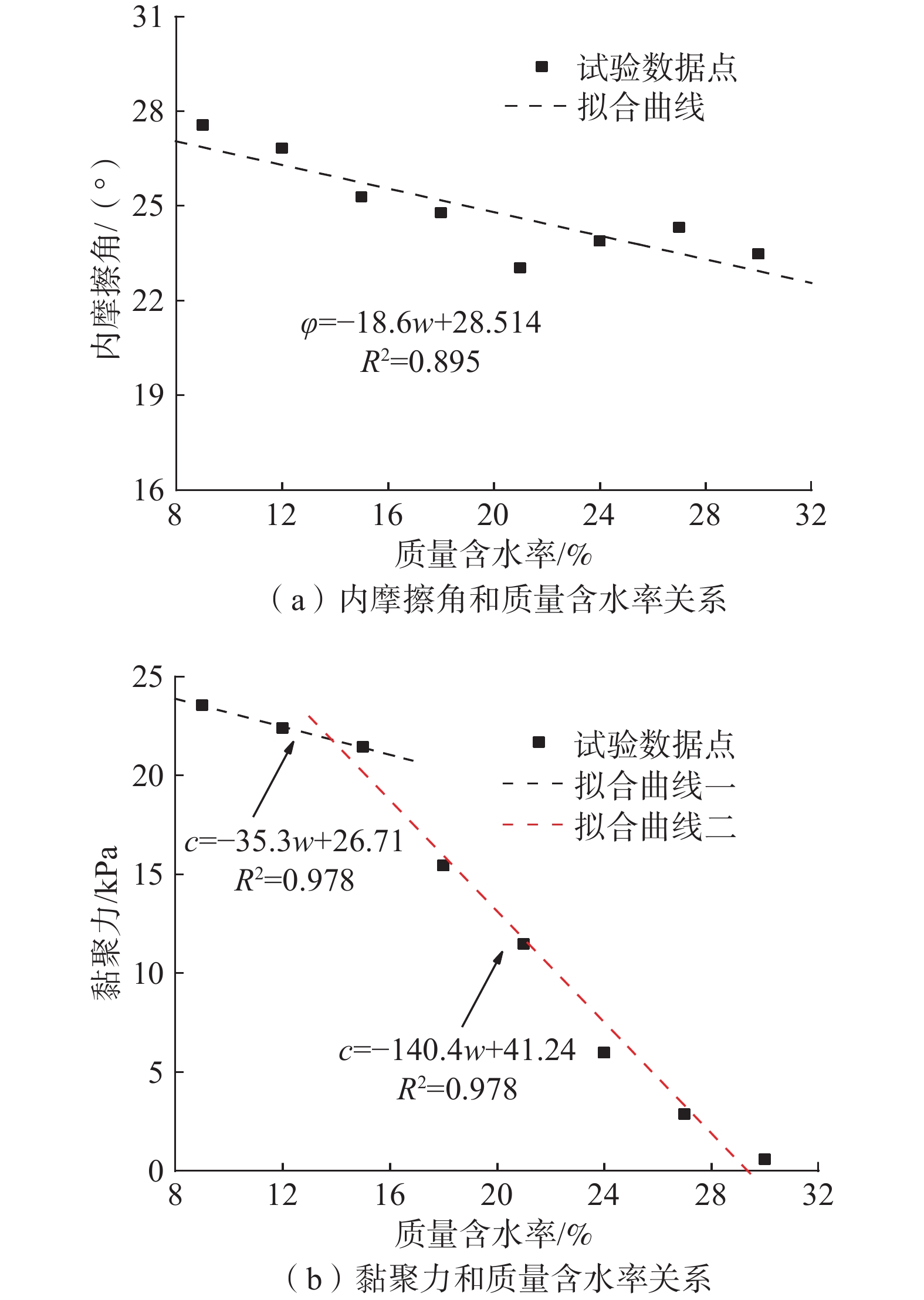
现采用剪切速率为0.8 mm/min的电动四联式等应变控制直剪仪(南京土壤仪器有限公司生产)进行不同含水率试样的直剪试验,取土深度约为1.5m,其土体抗剪强度参数随含水率的变化关系如图4所示。
由图4可知土体黏聚力在含水率15%~18%范围内发生突变,因此可采用分段式函数拟合黏聚力和含水率的关系。室内试验测得土体比重Gs=2.71,孔隙比e=0.82,根据饱和度Sr和含水率w之间的关系可得:
$$ \left\{ \begin{gathered} {{{c}}_{{1}}}{{ = }} - 10.7{{{S}} _{{{\rm{r}}}}}{{ + }}26.703,\;\;{{{S}} _{{{\rm{r}}}}} < 45.70\% \\ {{{c}}_{{2}}}{{ = }} - 42.5{{{S}} _{{{\rm{r}}}}}{{ + }}44.236,\;\;{{{S}} _{{{\rm{r}}}}} \geqslant 45.70\% \\ \end{gathered} \right. $$ (8) $$ \varphi {\text{ = }} - 5.6{{{S}}_{\text{r}}}{\text{ + }}28.541 $$ (9) 式中:Sr——饱和度/%;
c1、c2——不同饱和度(含水率)条件下试样的总黏 聚力/kPa,c1为饱和度小于45.70%时试 样的总黏聚力,c2为饱和度大于或等于 45.70%时试样的总黏聚力;
φ——总内摩擦角/(°)。
Fredlund等[11]在1978年建立了非饱和土的双变量抗剪强度公式,其表达式为:
$$ {\tau _{{{\rm{f}}}}} = {{c'}} + \left( {\sigma - {{{u}}_{{{\rm{a}}}}}} \right)\tan \varphi ' + \left( {{{{u}}_{{{\rm{a}}}}} - {{{u}}_{{{\rm{w}}}}}} \right)\tan {\varphi ^{{{\rm{b}}}}} $$ (10) 式中:τf——非饱和土抗剪强度/kPa;
$ {{c'}} $ 、$ \varphi ' $ ——土体有效抗剪强度参数,单位分别为kPa 和°;$\sigma - {{{u}}_{\rm{a}}}$ ——净法向应力/kPa;${{{u}}_{\rm{a}}}$ ——孔隙气压力/kPa;${{{u}}_{\rm{w}}}$ ——孔隙水压力/kPa;${{{u}}_{\rm{a}}} - {{{u}}_{\rm{w}}}$ ——基质吸力/kPa;φb——受基质吸力影响的内摩擦角/(°)。
为将有效黏聚力和吸附强度叠加起来,可采用总黏聚力表示基质吸力影响下土体抗剪强度变化[12],其表达式为:
$$ {{c}} = {{c'}} + \left( {{{{u}}_{\rm{a}}} - {{{u}}_{\rm{w}}}} \right)\tan {\varphi ^{{{\rm{b}}}}} $$ (11) 式中:c——总黏聚力/kPa。
将式(11)代入式(10)可得修正后的Fredlund非饱和土抗剪强度公式为:
$$ {\tau _{{{\rm{f}}}}} = {{c}} + \left( {\sigma - {{{u}}_{\rm{a}}}} \right)\tan \varphi $$ (12) 将式(8)—(9)代入式(12)可建立以饱和度为变量的分段式抗剪强度公式和湿重度公式:
$$ \left\{ \begin{gathered} {\tau _{{{{\rm{f}}}}1}} = {{{c}}_1} + (\sigma - {{{u}}_{\rm{a}}})\tan \varphi \\ {\tau _{{{{\rm{f}}}}2}} = {{{c}}_2} + (\sigma - {{{u}}_{\rm{a}}})\tan \varphi \\ {\gamma _{{{\rm{w}}}}} = {\gamma _{{{\rm{d}}}}}(1 + 0.303{{{S}} _{{{\rm{r}}}}}) \\ \end{gathered} \right. $$ (13) 式中:rw——土体湿重度/(kN·m−3);
rd——土体干重度/(kN·m−3);
Sr——饱和度/%;
τf1、τf2——分段抗剪强度/kPa;
$(\sigma - {{{u}}_{\rm{a}}}) $ ——净法向应力/kPa;ua——孔隙气压力/kPa。
3. 数值模拟结果分析
3.1 路堑边坡浅层塌滑分析
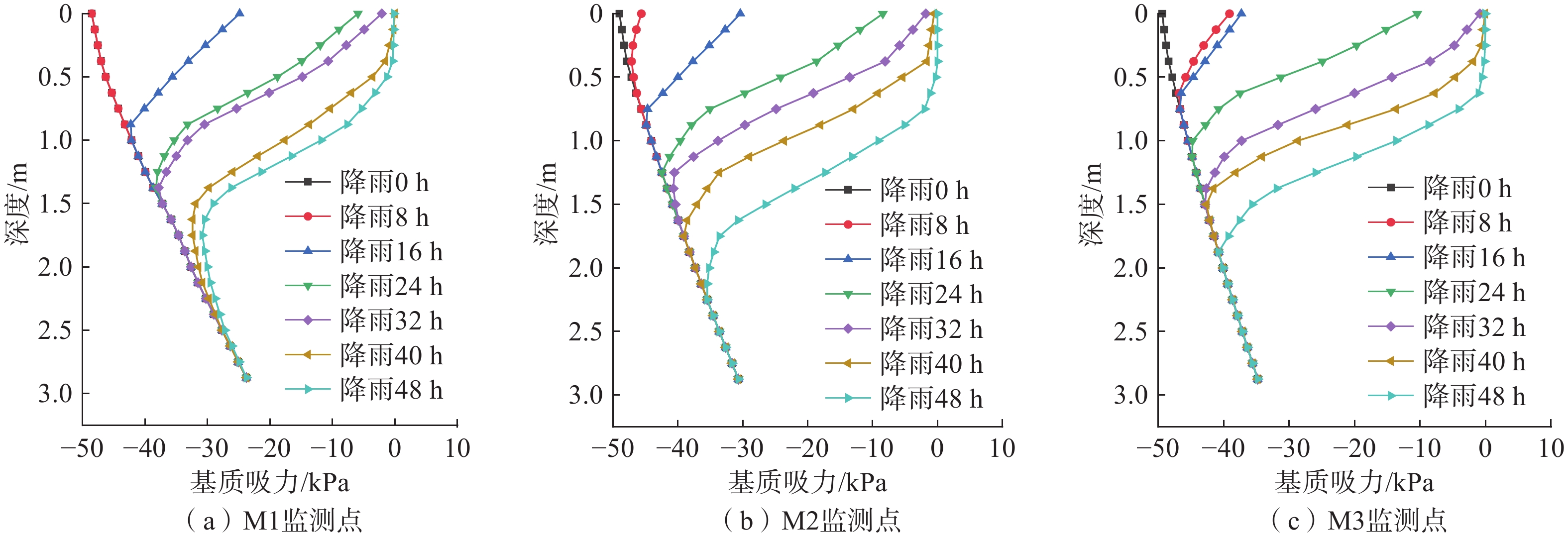
通过FLAC3D软件分别提取不同时刻下M1、M2和M3监测断面的孔隙水压力随深度的变化曲线(图5)。
由图5可知降雨过程中,M3监测断面(坡肩)土体的孔隙水压力最先开始变化,M1监测断面(坡脚)土体的孔隙水压力最后开始变化。降雨48 h时,边坡整体暂态饱和区成“J”型分布,其中M1、M3监测断面孔隙水压力变化深度分别为2.5 m和2 m,而M2(坡中)监测断面孔隙水压力变化深度和孔隙水压力开始变化时间均处于两者之间,综上所述可知坡脚部位的暂态饱和区深度高于坡肩。
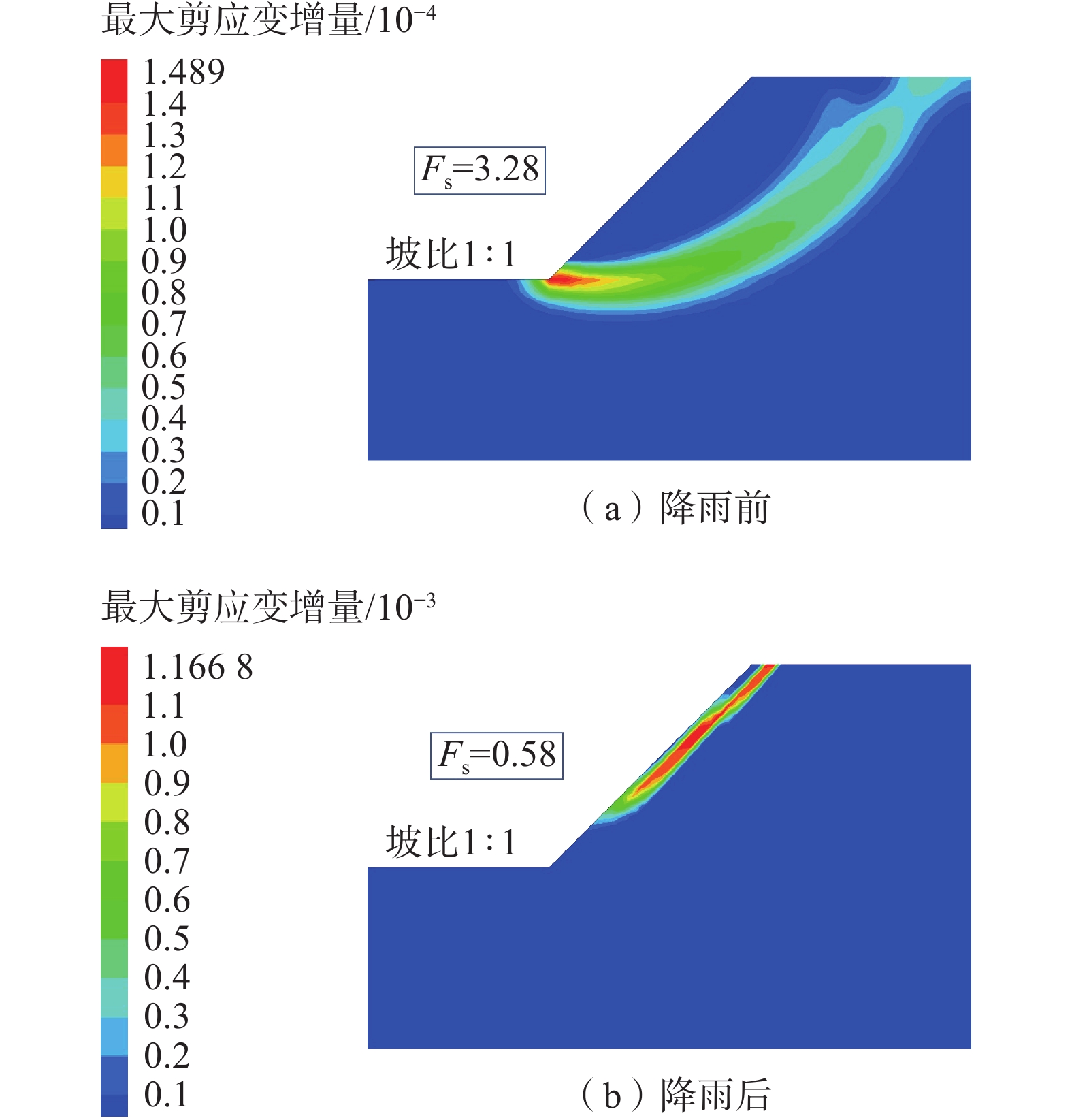
现基于强度折减法,通过FLAC3D数值软件可得到路堑边坡在降雨前后的最大剪应变增量云图(图6)。
由图6可以看出降雨过程中,路堑边坡的破坏模式由深层整体滑动向浅层局部滑动演化,降雨结束后,路堑边坡的安全系数(Fs)降低了82.32%,这是由于降雨入渗作用导致坡表土体内部孔隙水压力增加,有效应力降低,而且路堑边坡浅层土体由于含水率增加而导致自重增加,两者作用下最终导致坡体中上部浅层土体发生浅层塌滑,这也与现场浅层塌滑情况相吻合。
3.2 路堑边坡安全系数灰色关联度分析
降雨过程中,影响边坡稳定性的外界因素很多,其中降雨强度、坡比和降雨历时是最主要的外界影响因素[4,13]。现在原数值模拟基础上,通过FLAC3D软件分别计算不同坡比、降雨强度和降雨历时条件下边坡的安全系数(表3)。
表 3 边坡降雨前后安全系数Table 3. Safety factor of slope before and after rainfall坡比 降雨
强度/
(mm·h−1)降雨
历时/h初始安全
系数降雨结束时
安全系数1∶0.5 5 24 2.68 2.490 1∶0.75 5 24 2.92 2.750 1∶1 5 24 3.28 3.120 1∶1.25 5 24 3.30 3.180 1∶1 2.5 24 3.28 3.230 1∶1 5 24 3.28 3.120 1∶1 7.5 24 3.28 1.250 1∶1 10 24 3.28 1.110 1∶1 5 12 3.28 3.210 1∶1 5 24 3.28 3.120 1∶1 5 32 3.28 1.575 1∶1 5 48 3.28 0.580 降雨条件下,将边坡稳定性的评价标准可看成外界主要因素的影响函数,假定X1为坡比,X2为降雨强度,X3为降雨历时,降雨前后边坡安全系数变化幅度为Y,边坡安全系数的函数表达式为:
$$ {{{F}}_{{{\rm{s}}}}}{{ = f}}({{{X}}_1}{{,}}{{{X}}_2}{{,}}{{{X}}_3}) $$ (14) 现采用Matlab软件进行灰色关联度分析,根据表3可知外界主要影响因素构成的矩阵为:
$$ {\boldsymbol{X}}{\text{ = }}\left[ \begin{gathered} {X_1} \\ {X_2} \\ {X_3} \\ \end{gathered} \right] = \left[ {\begin{array}{*{20}{c}} 2 &1.33 &1 &0.8 \\ 2.5 &5 &7.5 &10 \\ 12 &24 &32 &48 \end{array}} \right] $$ (15) 降雨过程中边坡安全系数降低幅值矩阵为:
$$ {{{\boldsymbol{Y}} = }}\left[ \begin{gathered} {Y_1} \\ {Y_2} \\ {Y_3} \\ \end{gathered} \right] = \left[ {\begin{array}{*{20}{c}} 0.19 &0.17 &0.16 &0.12 \\ 0.05 &0.16 &2.03 &2.17 \\ 0.07 &0.16 &1.705 &2.7 \end{array}} \right] $$ (16) 分别对因变量矩阵数据和自变量矩阵数据进行均值无量纲和归一化可得:
$$ {\boldsymbol{X}}'{\text{ = }}\left[ \begin{gathered} {X'_1} \\ {X'_2} \\ {X'_3} \\ \end{gathered} \right] = \left[ {\begin{array}{*{20}{c}} 1.559 &1.037 &0.780 &0.624 \\ 0.4 &0.8 &1.2 &1.6\\ 0.4 &0.8 &1.2 &1.6 \end{array}} \right] $$ (17) $$ {{{\boldsymbol{Y}}' = }}\left[ \begin{gathered} {Y'_1} \\ {Y'_2} \\ {Y'_3} \\ \end{gathered} \right] = \left[ {\begin{array}{*{20}{c}} 1.187 &1.063 &1.000 &0.750 \\ 0.045 &0.145 &1.841 &1.968 \\ 0.060 &0.138 &1.471 &2.330 \end{array}} \right] $$ (18) 由式(17)—(18)可得差异序列矩阵
$\Delta_{{mn}} $ 为:$$ \Delta_{{mn}}{{ = }}\left[ {\begin{array}{*{20}{c}} 0.372 &0.025 &0.220 &0.126\\ 0.335 &0.655 &0.641 &0.368\\ 0.340 &0.662 &0.271 &0.730 \end{array}} \right] $$ (19) 根据式(19)可知m=0.022,M=0.663,根据式(6)可得到灰色关联系数矩阵为:
$$ {\boldsymbol{\xi }}{\text{ = }}\left[ {\begin{array}{*{20}{c}} 0.530 &1 &0.667 &0.795\\ 0.543 &0.383 &0.388 &0.533 \\ 0.554 &0.380 &0.614 &0.357 \end{array}} \right] $$ (20) 将式(20)代入式(7)可得到坡比、降雨强度和降雨历时三者与降雨过程中边坡安全系数降低幅度之间的关联度为:
$$ {{{\boldsymbol{r}}}}_{\rm{m}} = {\left[ {\begin{array}{*{20}{c}} {0.748}&{0.462}&{0.476} \end{array}} \right]^{{T}}} $$ (21) 由式(21)可知r1=0.748,r2=0.462,r3=0.476,因此r1>r3>r2,而又由于X1为坡比,X2为降雨强度,X3为降雨历时,故基于灰色关联理论可知坡比对降雨条件下的边坡安全系数影响最大,其余依次为降雨历时和降雨量。
3.3 不同坡比路堑边坡浅层破坏模式
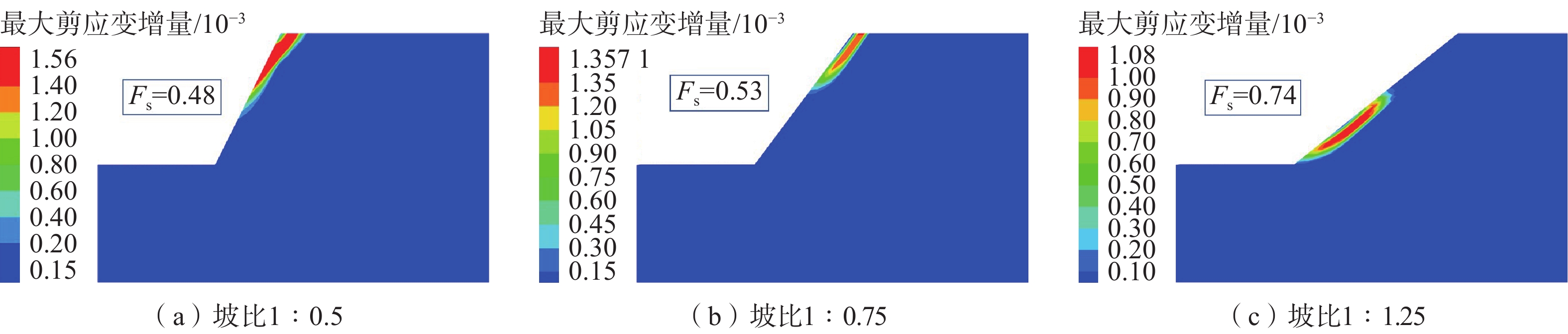
由于坡比是影响降雨条件下路堑边坡安全系数的最大敏感因子,因此在原数值模拟参数(降雨历时为48 h,降雨强度为5 mm/h,坡比为1∶1)基础上,通过FLAC3D软件分别提取降雨48 h后不同坡比的剪应变增量云图(图7)。
对比图6—7可知随着降雨历时的增加,路堑边坡潜在深层滑动面不断向浅层移动,且随着坡比的减小,浅层塌滑区区域逐渐由坡肩部位向坡脚部位移动。分析认为降雨过程中,坡面浅层孔隙水压力升高导致有效应力降低(图5),当路堑边坡的坡比较大时,坡肩冲蚀沟发育程度高,且降雨导致坡体浅层土体的抗剪强度降低,因此受重力因素影响,坡肩部位土体易向临空面发生浅层滑塌;当路堑边坡的坡比较小时,由于受上部土体重力以及坡体内部推力作用,浅层滑塌区域主要集中于坡脚部位;当路堑边坡的坡比值处于两者范围内,浅层滑塌最先开始于坡肩部位,然后逐渐向下延伸至坡面中部,最终形成坡体中上部区域浅层滑塌现象。
4. 室内不同坡度路堑边坡降雨试验
4.1 试验设计方案
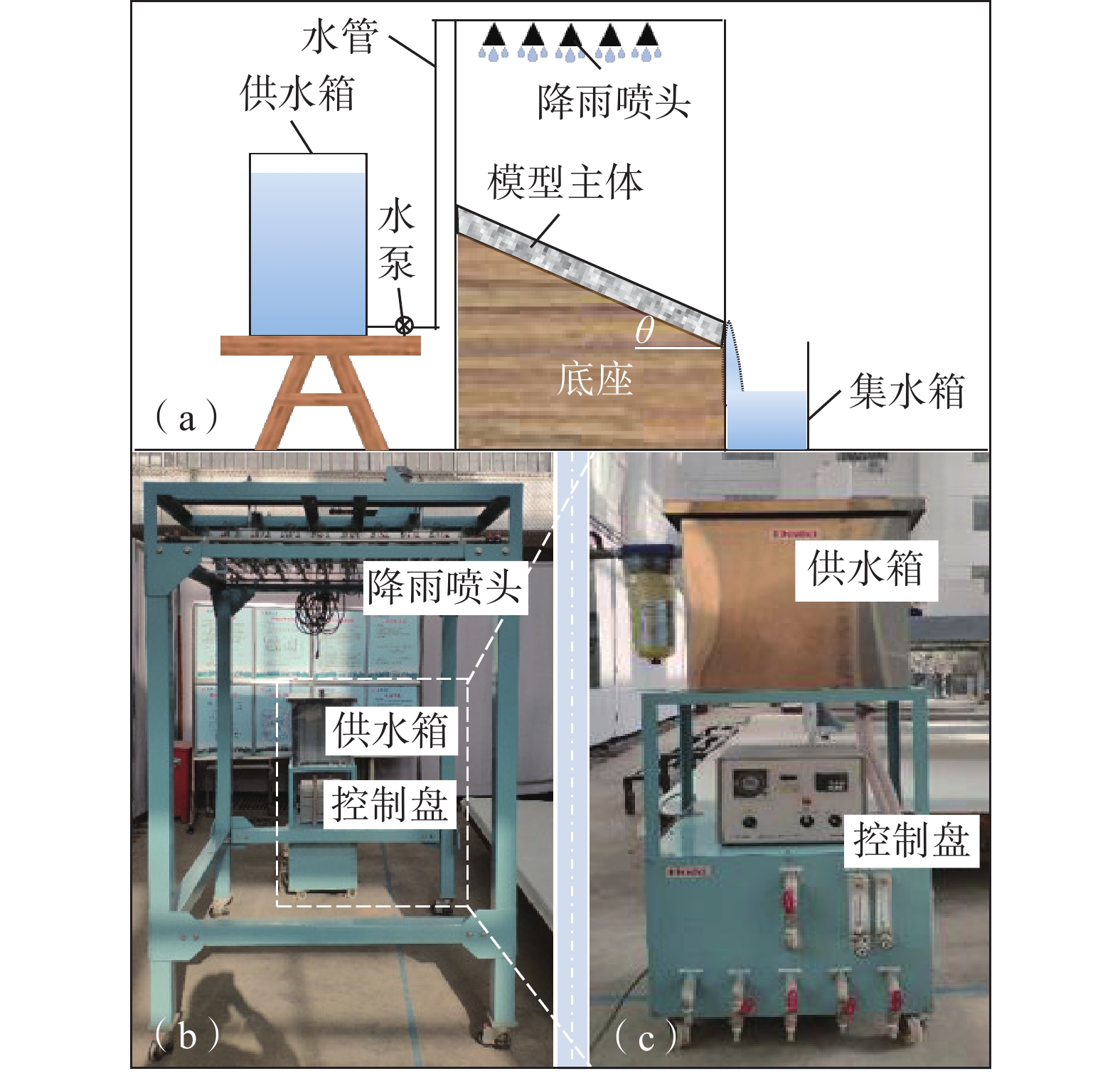
试验采用DIK-6000降雨器(图8)进行降雨模拟,仪器有效降雨面积S=1.0404 m2,降雨针管距地面高度为2 m,降雨强度范围为10~80 mm/h[14]。
试验主体部分为长方形模型,见图8(a),模型尺寸为长×宽×高=1.25 m×0.6 m×0.3 m,模型主体采用混凝土制成,土体与混凝土接触面设置隔水塑料板。在数值模拟基础上,将模型主体底部分别放在1∶1.5和1∶1.75坡比底座上,并结合现场防护条件(图1)设置无防护和拱骨架防护2种方案,其中拱骨架的拱圈半径设置为25 cm。坡体整体密度控制在1.89 g/cm3,试验降雨历时为1 h,试验降雨强度设为2 mm/min。
4.2 路堑边坡浅层破坏机制分析
室内降雨过程,由于水流回溯不断侵蚀粉质黏土坡面,而短时间雨水入渗量较少,因此表层土颗粒容易悬浮于水膜之中并被水流裹挟,在边坡表面留下鳞片状沟纹(图9),随着降雨历时的增加,坡面径流不断汇集,而溅击和片蚀而形成的坡面凹陷对水流具有引导作用,在侵蚀后期,径流将坡面表层土体进行软化,坡面凹陷更加明显。当水流冲蚀坡面时,水流回溯不断侵蚀沟槽下方,沟槽上方由于下方土体的流失,沟底土体不能承受上部土体的重力而发生浅层坍塌现象。对比无防护条件下的路堑边坡,拱骨架防护作用会改变径流的方向,减小坡面径流量,对坡面冲蚀具有一定减弱效果,因此拱骨架防护作用下坡脚部位土体强的度劣化程度较低,但在拱骨架的尖角,见图9(b1)和拱顶,见图9(b2)部位会出现土体溜滑现象。
为进一步分析不同坡比下拱骨架防护作用对边坡浅层土体冲蚀的影响,可引入累计冲蚀降低率[15],其表达式为:
$$ {\delta _t} = \frac{{{S _{{{tx}}}} - {S _{{{ty}}}}}}{{{S _{{{{tx}}}}}}} \times 100\% $$ (22) 式中:δt——t时刻累计冲蚀量降低率/%;
Stx——t时刻无防护条件下累计冲蚀量/kg;
Sty——t时刻拱骨架防护下累计冲蚀量/kg。
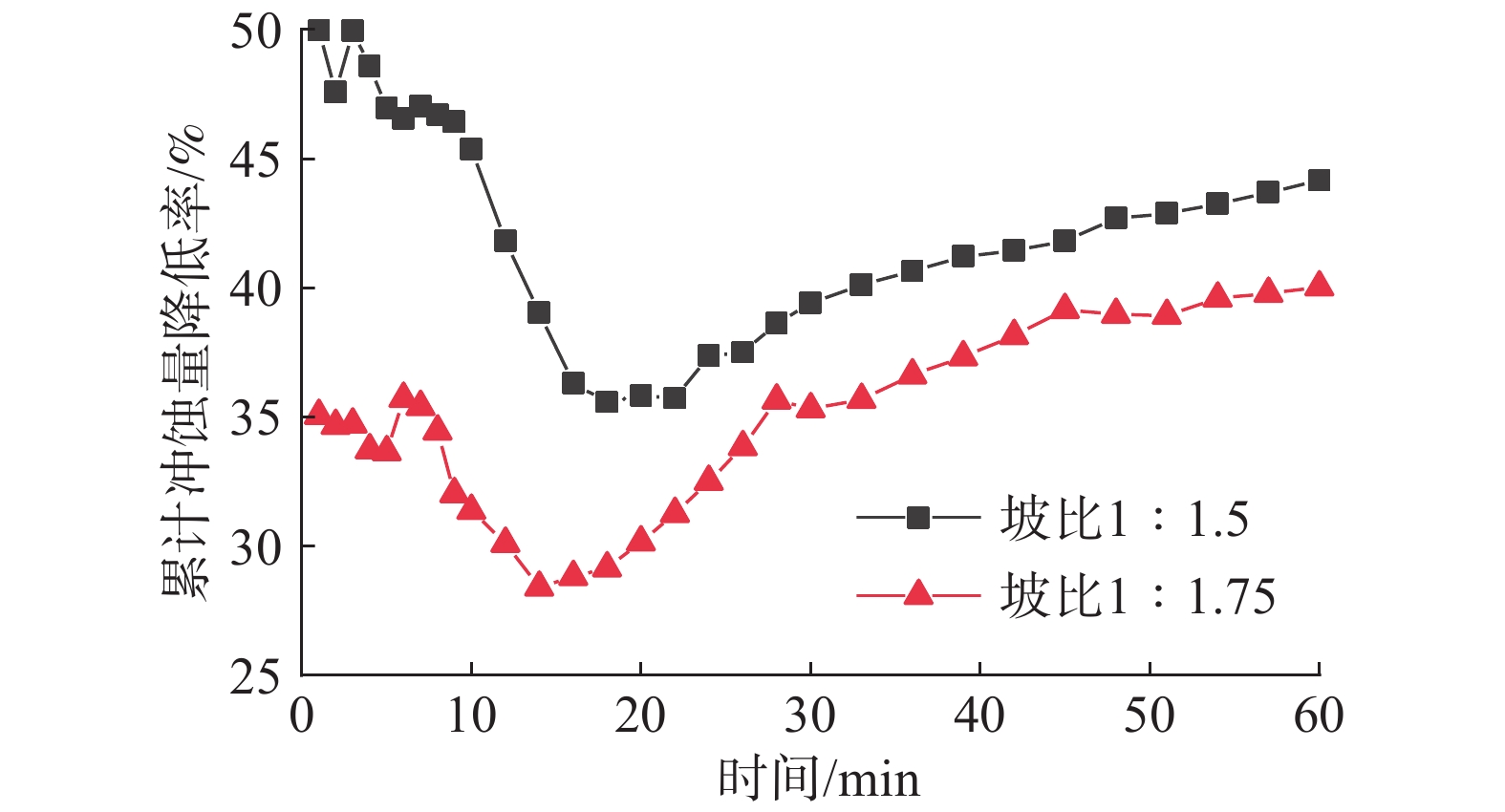
由式(22)可得到60 min时不同坡比下累计冲蚀量降低率变化如图10所示。由图10可知拱骨架防护对边坡冲蚀量具有一定抑制作用,在不同坡比条件下,浅层土体累计冲蚀率随时间增长均呈现出先降低后增加的趋势,且坡度越陡,边坡整体累计冲蚀降低率越大。分析认为拱骨架能提高坡体浅层土体的抗冲刷能力,在15 min降雨条件内,坡体浅层土体累计冲蚀量虽不断增加,但在拱骨架防护作用下,坡体浅层土体累计冲蚀量降低率在不断降低,这说明拱骨架在短时间内对抑制坡体浅层土体流失具有一定效果;在15~20 min范围内,坡体浅层土体处于饱和状态而发生软化现象;在20 min后,降雨导致路堑边坡浅层土体强度劣化程度增加,因此雨水更易裹挟土颗粒沿坡面流下,此时拱骨架的防护效果减弱,土体累计冲蚀量降低率不断增加。
5. 路堑边坡浅层塌滑生态防治措施
针对路堑边坡局部浅层塌滑以及拱骨架防护作用下小范围溜滑问题,生态材料防护是一种常见的治理措施[16]。为此,课题组在双达高速现场开展了小范围内生态防护材料试验,选取了4种国内外常见的生态防护材料进行对比分析,在人工搅拌后采用坡面播散或涂抹方法施工,不同材料类型及防护效果对比见表4[17],不同时刻路堑边坡浅层塌滑生态防治效果图见图11。
表 4 不同防护材料及防护效果对比Table 4. Comparison of different protective materials and their effectiveness防护材料名称 主要成分 质量配合比 草种添加量
/(g∙m−2)坡面防护层
厚度/mm路堑边坡浅层塌滑防治效果 HP-FGM
(灵活增长介质)卷曲纤维、木质纤维、
湿润剂和微孔颗粒16∶1∶2∶1 20 ≥30 坡面透气性和透水性最优,初期植被覆盖率最高,
短期内生态防治效果较优,长期应用表现一般素土 素土 — 20 ≥30 短期植被覆盖率一般,坡面透气性和透水性一般,
生态防治效果一般,长期应用表现一般EFM
(工程纤维基质)卷曲与木质纤维
和湿润剂8.1∶1 20 ≥30 坡面透气性和透水性良好,初期植被覆盖率较高,
短期内生态防治效果良好,长期应用表现一般聚丙烯纤维土 聚丙烯纤维
和素土0.003∶1 20 ≥30 坡面透气性和透水性最差,短期植被覆盖率最低,
短期生态防治效果较差,长期应用表现优良对比图11(a)—(e)可知HP-FGM与EFM防护下,短期内路堑边坡植被覆盖率高,而聚丙烯纤维土防护条件下,短期内植被覆盖率低。分析认为HP-FGM与EFM不需要控制压实度,具有较好的透气性和透水性,而边坡所在地降雨又比较充沛,有利于植物的前期快速生长,但聚丙烯纤维土中掺入加筋纤维,需要适当控制压实度,导致防护材料的抗剪强度增加和渗透性较低,故有利于植物的缓慢增长[18]。2019年7月9日,HP-FGM与EFM防护路堑边坡过程中,植被因失水出现一定程度枯萎,而在聚丙烯纤维土防护条件下,路堑边坡植被受影响较小[19 − 20]。2019年11月20日,坡体植被都处于枯萎状态,但对比发现HP-FGM和聚丙烯纤维土防护边坡坡面枯草长度和茂密程度相对较高,且聚丙烯纤维土防护边坡坡面枯草根部甚至保持青色,故聚丙烯纤维土边坡防护材料中植被生长速率虽然比HP-FGM和EFM慢一点,但聚丙烯纤维土边坡防护材料的长期应用表现最为理想。
6. 结 论
(1)土体黏聚力和内摩擦角均随含水率的增加而降低,其强度突变位置处于含水率为12%~18%对应的范围内,基于非饱和土抗剪强度理论可建立以饱和度为变量的分段式抗剪强度公式。
(2)基于灰色关联理论可知坡比、降雨历时和降雨量三者对路堑边坡浅层塌滑的影响程度中,坡比的影响程度最大,降雨历时次之,降雨强度最小。
(3)降雨过程中,路堑边坡潜在深层滑移面逐渐向坡体浅层转移,且浅层塌滑区域受路堑边坡坡比影响,当路堑边坡坡比高于1∶0.75时,边坡浅层塌滑区域靠近坡肩,当路堑边坡坡比低于1∶1.25时,边坡浅层塌滑区域靠近坡脚。
(4)室内降雨试验结果表明拱骨架防护作用会改变径流的方向,减小坡面径流量,对坡面冲蚀具有一定减弱效果,且在此基础上降低路堑边坡坡比对坡面冲蚀能起到进一步减弱效果。
(5)设计适宜的路堑边坡坡比能改变降雨引发的浅层塌滑区域,同时配合拱骨架和聚丙烯纤维加筋土防护作用能较好起到控制路堑边坡浅层塌滑类问题。
-
表 1 土体材料参数
Table 1 Basic physical parameters of undisturbed soil
弹性模量
/MPa泊松比 密度
/(g·cm−3)渗透系数
/(cm·s−1)有效黏聚力
/kPa有效内摩擦
角/(°)12.00 0.3 1.88 4.5×10-5 26.7 28.5 表 2 VG模型参数
Table 2 Summary table of VG model parameters
参数 θs θr α n R2 取值 0.4592 0.0837 0.0720 1.2661 0.9655 表 3 边坡降雨前后安全系数
Table 3 Safety factor of slope before and after rainfall
坡比 降雨
强度/
(mm·h−1)降雨
历时/h初始安全
系数降雨结束时
安全系数1∶0.5 5 24 2.68 2.490 1∶0.75 5 24 2.92 2.750 1∶1 5 24 3.28 3.120 1∶1.25 5 24 3.30 3.180 1∶1 2.5 24 3.28 3.230 1∶1 5 24 3.28 3.120 1∶1 7.5 24 3.28 1.250 1∶1 10 24 3.28 1.110 1∶1 5 12 3.28 3.210 1∶1 5 24 3.28 3.120 1∶1 5 32 3.28 1.575 1∶1 5 48 3.28 0.580 表 4 不同防护材料及防护效果对比
Table 4 Comparison of different protective materials and their effectiveness
防护材料名称 主要成分 质量配合比 草种添加量
/(g∙m−2)坡面防护层
厚度/mm路堑边坡浅层塌滑防治效果 HP-FGM
(灵活增长介质)卷曲纤维、木质纤维、
湿润剂和微孔颗粒16∶1∶2∶1 20 ≥30 坡面透气性和透水性最优,初期植被覆盖率最高,
短期内生态防治效果较优,长期应用表现一般素土 素土 — 20 ≥30 短期植被覆盖率一般,坡面透气性和透水性一般,
生态防治效果一般,长期应用表现一般EFM
(工程纤维基质)卷曲与木质纤维
和湿润剂8.1∶1 20 ≥30 坡面透气性和透水性良好,初期植被覆盖率较高,
短期内生态防治效果良好,长期应用表现一般聚丙烯纤维土 聚丙烯纤维
和素土0.003∶1 20 ≥30 坡面透气性和透水性最差,短期植被覆盖率最低,
短期生态防治效果较差,长期应用表现优良 -
[1] WANG Genlong,LI Tonglu,XING Xianli,et al. Research on loess flow-slides induced by rainfall in July 2013 in Yan’an,NW China[J]. Environmental Earth Sciences,2014,73(12):7933 − 7944. DOI: 10.1007/s12665-014-3951-9
[2] 李同录,李颖喆,赵丹旗,等. 对水致黄土斜坡破坏模式及稳定性分析原则的思考[J]. 中国地质灾害与防治学报,2022,33(2):25 − 32. [LI Tonglu,LI Yingzhe,ZHAO Danqi,et al. Thoughts on modes of loess slope failure triggered by water infiltration and the principals for stability analysis[J]. The Chinese Journal of Geological Hazard and Control,2022,33(2):25 − 32. (in Chinese with English abstract) LI Tonglu, LI Yingzhe, ZHAO Danqi, et al. Thoughts on modes of loess slope failure triggered by water infiltration and the principals for stability analysis[J]. The Chinese Journal of Geological Hazard and Control, 2022, 33(2): 25-32. (in Chinese with English abstract)
[3] 石诚鋆,阮永芬,施炳军,等. 降雨入渗对边坡稳定性影响的敏感性分析[J]. 防灾减灾工程学报,2016,36(6):1002 − 1007. [SHI Cheng,RUAN Yongfen,SHI Bingjun,et al. The sensitivity analysis of influence of rainfall infiltration on landslide stability[J]. Journal of Disaster Prevention and Mitigation Engineering,2016,36(6):1002 − 1007. (in Chinese with English abstract) DOI: 10.13409/j.cnki.jdpme.2016.06.022 SHI Cheng, RUAN Yongfen, SHI Bingjun, et al. The sensitivity analysis of influence of rainfall infiltration on landslide stability[J]. Journal of Disaster Prevention and Mitigation Engineering, 2016, 36(6): 1002-1007. (in Chinese with English abstract) DOI: 10.13409/j.cnki.jdpme.2016.06.022
[4] 蔡荣坤,戴自航,徐根连,等. 降雨对花岗岩风化层路堑边坡滑动模式影响—以福建云平高速云霄段为例[J]. 中国地质灾害与防治学报,2021,32(2):27 − 35. [CAI Rongkun,DAI Zihang,XU Genlian,et al. Influence of rainfall on sliding modes of cutting slope of weathered granite stratum:Taking Yunxiao section in the Yunping freeway in Fujian for example[J]. The Chinese Journal of Geological Hazard and Control,2021,32(2):27 − 35. (in Chinese with English abstract) CAI Rongkun, DAI Zihang, XU Genlian, et al. Influence of rainfall on sliding modes of cutting slope of weathered granite stratum: taking Yunxiao section in the Yunping freeway in Fujian for example[J]. The Chinese Journal of Geological Hazard and Control, 2021, 32(2): 27-35. (in Chinese with English abstract)
[5] 孙萍萍,张茂省,江睿君,等. 降雨诱发浅层黄土滑坡变形破坏机制[J]. 地质通报,2021,40(10):1617 − 1625. [SUN Pingping,ZHANG Maosheng,JIANG Ruijun,et al. Deformation and failure mechanism of rainfall-induced shallow loess landslide[J]. Geological Bulletin of China,2021,40(10):1617 − 1625. (in Chinese with English abstract) DOI: 10.12097/j.issn.1671-2552.2021.10.003 SUN Pingping, ZHANG Maosheng, JIANG Ruijun, et al. Deformation and failure mechanism of rainfall-induced shallow loess landslide[J]. Geological Bulletin of China, 2021, 40(10): 1617-1625. (in Chinese with English abstract) DOI: 10.12097/j.issn.1671-2552.2021.10.003
[6] 胡华,吴轩,张越. 基于模拟试验的强降雨条件下花岗岩残积土斜坡滑塌破坏机理分析[J]. 中国地质灾害与防治学报,2021,32(5):92 − 97. [HU Hua,WU Xuan,ZHANG Yue. Experimental study on slope collapse characteristics of granite residual soil slope under heavy rainfall[J]. The Chinese Journal of Geological Hazard and Control,2021,32(5):92 − 97. (in Chinese with English abstract) HU Hua, WU Xuan, ZHANG Yue. Experimental study on slope collapse characteristics of granite residual soil slope under heavy rainfall[J]. The Chinese Journal of Geological Hazard and Control, 2021, 32(5): 92-97. (in Chinese with English abstract)
[7] 杜忠原,葛忻声,仝飞. 不同降雨条件下高边坡的稳定性分析[J]. 科学技术与工程,2021,21(30):13039 − 13045. [DU Zhongyuan,GE Xinsheng,TONG Fei. Stability analysis of high slope under different rainfall conditions[J]. Science Technology and Engineering,2021,21(30):13039 − 13045. (in Chinese with English abstract) DOI: 10.3969/j.issn.1671-1815.2021.30.034 DU Zhongyuan, GE Xinsheng, TONG Fei. Stability analysis of high slope under different rainfall conditions[J]. Science Technology and Engineering, 2021, 21(30): 13039-13045. (in Chinese with English abstract) DOI: 10.3969/j.issn.1671-1815.2021.30.034
[8] 李宁,赫建勇,许建聪,等. 降雨条件下抗滑桩边坡稳定性影响的数值分析[J]. 水利水电技术,2020,51(4):1 − 9. [LI Ning,HE Jianyong,XU Jiancong,et al. Numerical analysis on stability of anti-slide pile slope under rainfall condition[J]. Water Resources and Hydropower Engineering,2020,51(4):1 − 9. (in Chinese with English abstract) LI Ning, HE Jianyong, XU Jiancong, et al. Numerical analysis on stability of anti-slide pile slope under rainfall condition[J]. Water Resources and Hydropower Engineering, 2020, 51(4): 1-9. (in Chinese with English abstract)
[9] 邓聚龙. 灰理论基础[M]. 武汉: 华中科技大学出版社, 2002 DENG Julong. Basis of grey theory[M]. Wuhan: Huazhong University of Science and Technology Press, 2002. (in Chinese)
[10] VAN GENUCHTEN M T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils[J]. Soil Science Society of America Journal,1980,44(5):892 − 898. DOI: 10.2136/sssaj1980.03615995004400050002x
[11] FREDLUND D G,MORGENSTERN N R,WIDGER R A. The shear strength of unsaturated soils[J]. Canadian Geotechnical Journal,1978,15(3):313 − 321. DOI: 10.1139/t78-029
[12] 饶鸿,王金淑,赵志明,等. 基于有限元软件自定义本构模型的膨胀土边坡降雨入渗分析[J]. 水文地质工程地质,2021,48(1):154 − 162. [RAO Hong,WANG Jinshu,ZHAO Zhiming,et al. An analysis of rainfall infiltration of expansive soil slope based on the finite element software custom constitutive model[J]. Hydrogeology & Engineering Geology,2021,48(1):154 − 162. (in Chinese with English abstract) RAO Hong, WANG Jinshu, ZHAO Zhiming, et al. An analysis of rainfall infiltration of expansive soil slope based on the finite element software custom constitutive model[J]. Hydrogeology & Engineering Geology, 2021, 48(1): 154-162. (in Chinese with English abstract)
[13] 黄明奎,马璐. 极端降雨对边坡土体强度的影响及其稳定性分析[J]. 灾害学,2021,36(3):6 − 9. [HUANG Mingkui,MA Lu. Stability and soil strength analysis of alope under extreme rainfall[J]. Journal of Catastrophology,2021,36(3):6 − 9. (in Chinese with English abstract) HUANG Mingkui, MA Lu. Stability and soil strength analysis of alope under extreme rainfall[J]. Journal of Catastrophology, 2021, 36(3): 6-9. (in Chinese with English abstract)
[14] 原泽,晏长根,陶悦,等. 骨架防护黄土边坡坡面冲蚀模型试验研究[J]. 工程地质学报,2023,31(6):1989 − 1998. [YUAN Ze,YAN Changgen,TAO Yue,et al. Erosion model test of loess slope with the framework protection[J]. Journal of Engineering Geology,2023,31(6):1989 − 1998. (in Chinese with English abstract) YUAN Ze, YAN Changgen, TAO Yue, et. al. Erosion model test of loess slope with the framework protection[J].Journal of Engineering Geology.2023,31(6):1989-1998. (in Chinese with English abstract)
[15] 晏长根,杨晓华,谢永利,等. 土工格室对黄土路堤边坡抗冲刷的试验研究[J]. 岩土力学,2005,26(8):1342 − 1344. [YAN Changgen,YANG Xiaohua,XIE Yongli,et al. Experimental research on anti-eroding effect of geocells in loess embankment[J]. Rock and Soil Mechanics,2005,26(8):1342 − 1344. (in Chinese with English abstract) DOI: 10.16285/j.rsm.2005.08.034 YAN Changgen, YANG Xiaohua, XIE Yongli, et al. Experimental research on anti-eroding effect of geocells in loess embankment[J]. Rock and Soil Mechanics, 2005, 26(8): 1342-1344. (in Chinese with English abstract) DOI: 10.16285/j.rsm.2005.08.034
[16] 汪益敏,陶玥琛,程致远,等. 高速公路路堑边坡客土喷播的长期防护效果[J]. 生态环境学报,2021,30(8):1724 − 1731. [WANG Yimin,TAO Yuechen,CHENG Zhiyuan,et al. Long-term protective effect of external-soil spray seeding on highway cutting slope[J]. Ecology and Environmental Sciences,2021,30(8):1724 − 1731. (in Chinese with English abstract) [WANG Yimin, TAO Yuechen, CHENG Zhiyuan, et al. Long-term protective effect of external-soil spray seeding on highway cutting slope[J]. Ecology and Environmental Sciences, 2021, 30(8): 1724-1731. (in Chinese with English abstract)
[17] 谭明健,周春梅,孙东,等. 软硬互层顺层岩质边坡破坏试验[J]. 地质科技通报,2022,41(2):274 − 281, 324. [TAN Mingjian,ZHOU Chunmei,SUN Dong, et al. Failure experiment of soft-hard interlayer bedding rock slope[J]. Bulletin of Geological Science and Technology,2022,41(2):274 − 281, 324. (in Chinese with English abstract) TAN Mingjian, ZHOU Chunmei, SUN Dong, et al. Failure experiment of soft-hard interlayer bedding rock slope[J]. Bulletin of Geological Science and Technology, 2022, 41(2): 274-281, 324. (in Chinese with English abstract)
[18] 罗晓娟, 寇桓嘉, 祝国强, 等. 断层破碎带条件下组合式圆截面抗滑桩加固边坡效果研究[J]. 地质科技通报,2022,41(6):253 − 261. [LUO Xiaojuan, KOU Huanjia, ZHU Guoqiang, et al. Effect of combined anti-slide piles with circular section to reinforce the slope containing the fault crushed zone[J]. Bulletin of Geological Science and Technology,2022,41(6):253 − 261. (in Chinese with English abstract) LUO Xiaojuan, KOU Huanjia, ZHU Guoqiang, et al. Effect of combined anti-slide piles with circular section to reinforce the slope containing the fault crushed zone[J]. Bulletin of Geological Science and Technology, 2022, 41(6): 253-261. (in Chinese with English abstract)
[19] 石爱红, 李国庆, 丁德民, 等. 考虑非饱和土基质吸力的丁家坡滑坡变形机制及稳定性评价[J]. 水文地质工程地质,2022,49(6):141 − 151. [SHI Aihong, LI Guoqing, DING Demin, et al. Deformation mechanism and stability evaluation of Dingjiapo landslide considering the matric suction of unsaturated soil[J]. Hydrogeology & Engineering Geology,2022,49(6):141 − 151. (in Chinese with English abstract) SHI Aihong, LI Guoqing, DING Demin, et al. Deformation mechanism and stability evaluation of Dingjiapo landslide considering the matric suction of unsaturated soil[J]. Hydrogeology & Engineering Geology, 2022, 49(6): 141-151.(in Chinese with English abstract)
[20] 徐文刚, 余旭荣, 年廷凯, 等. 基于FLAC3D的三维边坡稳定性强度折减法计算效率改进算法及其应用[J]. 吉林大学学报(地球科学版),2021,51(5):1347 − 1355. [XU Wengang, YU Xurong, NIAN Tingkai, et al. Optimization and application of FLAC3D strength-reduction computation in three-dimension slope stability analysis[J]. Journal of Jilin University (Earth Science Edition),2021,51(5):1347 − 1355. (in Chinese with English abstract) XU Wengang, YU Xurong, NIAN Tingkai, et al. Optimization and application of FLAC3D strength-reduction computation in three-dimension slope stability analysis[J]. Journal of Jilin University (Earth Science Edition), 2021, 51(5): 1347-1355.(in Chinese with English abstract)





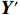
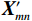
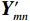
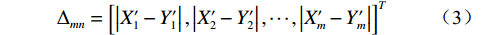
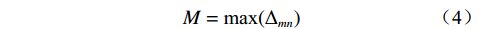
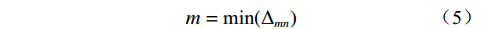
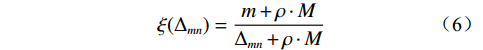
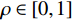
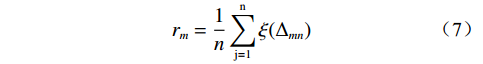

 下载:
下载:
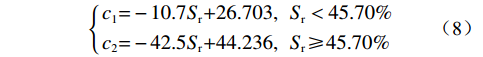
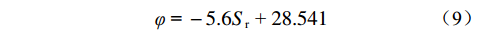
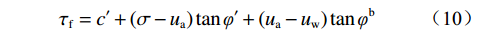
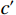
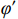
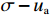
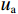
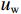
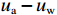
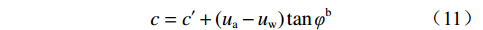
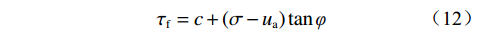
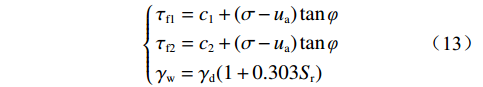
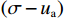
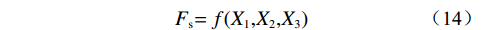
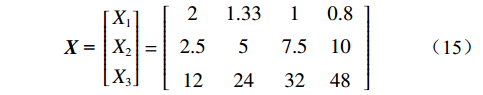
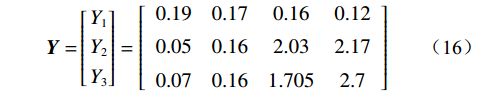
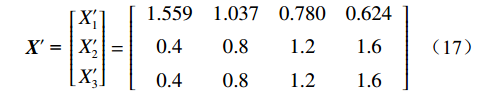
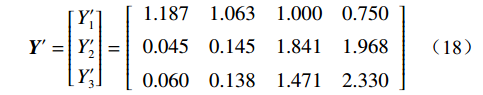
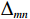
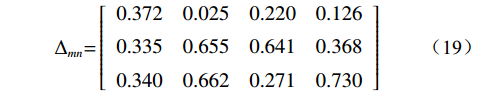

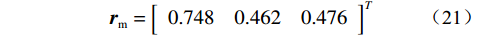

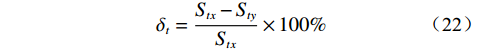

 邮件订阅
邮件订阅 RSS
RSS