Open-pit mine slopes stability analysis based on analytic hierarchy process-fuzzy comprehensive evaluation model
-
摘要:
露天煤矿台阶所构成的边坡对矿山资源生产及运输发挥着重要的作用，也承载着煤炭外运的任务，其稳定性对矿山连续生产具有重要意义。文章在边坡地质调查和监测信息分析的基础上，充分考虑边坡几何形态、地质信息、气象水文信息、现场监测信息等指标，以层次分析法确定边坡稳定性分析的指标权重，基于隶属度最大原则确定边坡稳定性状态，建立了多源信息融合的边坡层次分析-模糊综合评价模型。将该模型应用于扎哈淖尔露天煤矿北帮边坡稳定性分析中，最后基于数值模拟对模型进行了验证。研究表明，北帮边坡基本稳定，基于数值模拟得出扎哈淖尔露天煤矿北帮边坡滑移面安全系数为1.121，模型结果与数值模拟结果所得到的边坡稳定性状态吻合度较好，验证了模型的有效性。该模型可以充分考虑多重信息对边坡稳定性分析的贡献，从而更全面准确分析边坡稳定性。
Abstract:The bench slope within an open-pit coal mine plays an important supporting role for coal resource production and transportation. The stability evaluation of the slope is of great significance in guiding continuous mining operations within the mine. This study leverages monitoring data and geological surveys of the slope, employing the analytic hierarchy process (AHP) to assign weights to slope stability analysis factors. Additionally, it employs the principle of maximum membership degree, taking into account various parameters such as slope geometry, geological data, meteorological and hydrological information, and field monitoring data. This paper establishes an analytic hierarchy process - fuzzy comprehensive evaluation model for slope stability assessment. Subsequently, the model is applied to analyze the stability of the north slope at the Zhahanao’er open-pit coal mine. The research indicates that, accordingly to the established slope analytic hierarchy process - fuzzy comprehensive evaluation model, the northern slope is deemed to be fundamentally stable. The numerical simulated FOS (factor of safety) of 1.121 aligns remarkably well with model results. It is comprehensive and accurate since the model can fully consider the contribution of multiple information to the stability of slope.
-
0. 引言
地基稳定性受多种因素影响[1 − 2]，特别是黄土地区，受震陷影响很大。黄土震陷作为一种严重的地质灾害，一旦发生将会造成非常严重的后果。前人对与黄土震陷的研究基本是以动三轴试验为主，以单个震陷量作为震陷性的主要的评价指标[3 − 6]。然而黄土地基震陷的准确性评价受到土性参数不确定性的影响，其中物理力学指标的概率分布类型和变异性会对评价结果产生影响。针对岩土工程中参数、计算模型、荷载等不确定性问题，其主要的不确定性分析方法包括：概率分析方法[7]、随机有限元法[8]、灰色系统评价法[9]、模糊数学法[10]、神经网络评价方法[11]等。这些不确定性方法可以考虑得更加全面，从而提高评价结果的准确性，使结果更为科学合理。
关于黄土震陷在不确定性方面的研究，李波等[12]采用灰色关联方法和逐步判别方法建立了耦合式软土震陷判别模型从而实现软土震陷等级的判定。在黄土震陷概率评价方面，谭芳[13]将概率地震危险性分析方法引入震陷计算中，采用不确定性分析方法分析了黄土震陷与地震参数之间的关系，从而提出一种考虑地震随机性的黄土震陷预测方法。任森等[14]基于大量动三轴试验，结合场地地震危险性概率分析方法，确定了研究区内的震陷区划。孙军杰等[15]依据残余应变估算模型采用概率统计等非确定性分析方法对地基动力沉降进行了概率分析。可见概率分析方法在土体动力沉降中已经得到了初步研究。
然而到目前为止，还没有研究将可靠度理论应用于黄土地基震陷的分析中。因此本文尝试将可靠度理论应用于黄土地基震陷评价中，使用可靠度方法对黄土地基震陷性进行分析。可靠度方法和传统的确定性分析方法相互补充与结合，有助于进行震陷可靠度分析。
1. 黄土地基震陷可靠度指标
可靠度理论在边坡稳定分析中被广泛应用，而边坡工程的不确定因素主要为土体参数的抗剪强度（内摩擦角、黏聚力）[16 − 18]。其依托蒙特卡洛分析法通过计算出多组安全系数值将小于1的安全系数的次数与计算次数的比值称作失效概率。因此可求得对应的可靠度指标（$ \mathrm{\beta } $）为：
$$ \beta ={\varPhi }^{-1}(1-{P}_{\text{f}}) $$ (1) 式中：$ \varPhi $——标准正态分布的累计分布函数；
${P_{\text{f}}}$——失效概率。
在目前已有的地震灾害评估中，尚未有关于地基震陷量的标准划分依据。根据中国地震局发布的《震害调查及地震损失评定工作指南》，可以采用“地基基础破坏等级标准”来评估震陷灾害的程度[16]，将震陷量小于2 cm的定义为基本完好，震陷量大于40 cm的定义为破坏。
参考可靠度理论在边坡稳定性评价中的应用，结合黄土动力学对震陷等级的划分，本文提出了一种对黄土地基震陷评价的可靠度指标。
（1）最大可靠度
在震陷等级划分中将震陷量大于40 cm的定义为震陷破坏，因此可采用破坏概率（Pd）来判定其震陷破坏状态，即$ {P_{\mathrm{d}}} = P\left( {S \geqslant 40} \right) $。将$ \beta_{\mathrm{d}} $定义为：
$$ {\beta _{\mathrm{d}}} = \frac{{40 - {u_{\mathrm{s}}}}}{{{\sigma _{\mathrm{s}}}}} $$ (2) 式中：$ {u_{\mathrm{s}}} $——震陷量的平均值；
$ {\sigma _{\mathrm{s}}} $——震陷量的标准差。
如果震陷量符合标准正态分布，破坏概率与可靠度的关系可表示为：
$$ {P_{\mathrm{d}}} = P\left( {S > 40} \right) = 1 - \varPhi \left(\frac{{40 - {u_{\mathrm{s}}}}}{{{\sigma _{\mathrm{s}}}}}\right) = 1 - \varPhi ({\beta _{\mathrm{d}}}) $$ (3) 则根据可靠度理论，将破坏概率对应的可靠度称为最大可靠度（${\beta }_{\text{d}} $），也就是指衡量地基震陷最大安全程度的标准，其计算公式为：
$$ {\beta }_{\text{d}}={\varPhi }^{-1}(1-{P}_{\text{d}}) $$ (4) 根据蒙特卡罗可靠度计算方法可定义破坏概率为：
$$ {P_{\text{d}}} = \frac{M}{N} $$ (5) 式中：$ {P}_{{\mathrm{d}}} $——地基震陷破坏概率；
M——抽样次数中震陷量大于40 cm的次数；
N——蒙特卡洛分析法总的抽样次数。
（2）最小可靠度
在震陷等级划分中将震陷量小于2 cm的定义为基本完好，因此可采用完好概率（Ph）来判定其完好状态，即$ {P_{\mathrm{h}}} = P\left( {S \leqslant 2} \right) $。将$ {\beta _{\mathrm{h}}} $定义为：
$$ {\beta _{\mathrm{h}}} = \frac{{2 - {u_{\mathrm{s}}}}}{{{\sigma _{\mathrm{s}}}}} $$ (6) 式中：$ {u_{\mathrm{s}}} $——震陷量的平均值；
$ {\sigma _{\mathrm{s}}} $——震陷量的标准差。
如果震陷量符合标准正态分布，完好概率（Ph）与可靠度的关系可表示为：
$$ {P_{\mathrm{h}}} = P\left( {S < 2} \right) = \varPhi \left(\frac{{2 - {u_{\mathrm{s}}}}}{{{\sigma _{\mathrm{s}}}}}\right) = \varPhi ({\beta _{\mathrm{h}}}) $$ (7) 根据可靠度理论，将完好概率对应的可靠度称为最小可靠度（${\beta _{\mathrm{h}}} $），也就是指衡量地基震陷完好程度的标准，其计算公式为：
$$ {\beta _{\text{h}}} = {\varPhi ^{ - 1}}\left( {{P_{\text{h}}}} \right) $$ (8) 根据蒙特卡罗可靠度计算方法可定义完好概率为：
$$ {P_{\text{h}}} = \frac{M}{N} $$ (9) 式中：$ {P}_{{\mathrm{h}}} $——地基完好概率；
M——抽样次数中震陷量小于2 cm的次数；
N——蒙特卡洛分析法总的抽样次数。
2. 基于Kriging代理模型的震陷可靠度计算
2.1 Kriging代理模型的建立
Kriging模型是一种基于方差最小的无偏估计方法，它的原理是通过已知样本点的线性加权法来预测未知点的函数值，即已知加权系数插值就可求得变量空间内任一点的函数值。Kriging代理模型通常情况下由回归部分和随机误差两部分所组成。将其用输出变量S(x)与输入变量x表示为：
$$ S({\boldsymbol{x}}) = \sum\limits_{i = 1}^m {{\beta _i}} f({\boldsymbol{x}}) + {\textit{z}}({\boldsymbol{x}}) = f{({\boldsymbol{x}})^T}{\boldsymbol{\beta}} + {\textit{z}}({\boldsymbol{x}}) $$ (10) 式中：每个样本点中输入变量的个数为n，$ {\boldsymbol{x}} = [ {x_1},{x_2}, \cdots , {x_n} ]^T$，$ f(x) = {\left[ {{f_1}(x),{f_2}(x), \cdots ,{f_m}(x)} \right]^T} $为回归多项式基函数向量，m为回归多项式的数量；${\boldsymbol{\beta}} = {[{\beta _1},{\beta _2},\cdots,{\beta _m}]^T}$为多项式参数向量，z(x)为一均值为0，方差为$ {\sigma ^2} $的正态随机过程，该随机过程的协方差为：
$$ COV\left[{\textit{z}}(u),{\textit{z}}(v)\right]={\sigma }^{2}R({u,v}) $$ (11) 其中，R表示任意两点u，v的相关函数，通常取为高斯相关方程，即：
$$ R(u,v) = \exp \left\{ { - \theta {{(u - v)}^2}} \right\} $$ (12) 其中，$ \theta $为相关参数，可通过最大似然估计得到：
$$ \theta=\max \left\{ { - \left[ {\frac{1}{2}\ln \left( {\left| R \right|} \right)} \right] + \frac{k}{2}\ln \left( {{\sigma ^2}} \right)} \right\} $$ (13) 其中，R为相关矩阵，元素R=R(u,v)。
基于给定的样本点，多项式参数向量$\beta $与随机过程方差$ {\sigma ^2} $的估计值分别为：
$$ \left\{ {\begin{split} & {\hat {\boldsymbol{\beta}} = {{\left( {{{\boldsymbol{F}}^T}{{\boldsymbol{R}}^{ - 1}}{\boldsymbol{F}}} \right)}^{ - 1}}{{\boldsymbol{F}}^T}{{\boldsymbol{R}}^{ - 1}}{\boldsymbol{Y}}} \\ & {{{\hat {\boldsymbol{\sigma}} }^2} = \frac{1}{k}{{\left( {{\boldsymbol{Y}} - {\boldsymbol{F}}\hat {\boldsymbol{\beta}} } \right)}^T}{{\boldsymbol{R}}^{ - 1}}\left( {{\boldsymbol{Y}} -{\boldsymbol{ F}}\hat {\boldsymbol{\beta}} } \right)} \end{split}} \right. $$ (14) 其中，F为由回归多项式函数值构成的矩阵。
对于任意输入变量$ {x_0} $,假定$ {x_0} $与输入变量样本X之间的相关系数向量为$ {{\boldsymbol{r}}_0} = {\left[ {R\left( {{x_0},{x_1}} \right), \cdots ,R\left( {{x_0},{x_k}} \right)} \right]^T} $利用式（10）构建的Kriging模型表达式，可以得到与$ {x_0} $对应的系统响应值$ S({x_0}) $的预测值$ \hat S({x_0}) $服从正态分布$ N(\hat S({x_0}),{\hat \sigma _{\hat S}}^2({x_0})) $,$ S({x_0}) $的最佳线性无偏估计及均方误差可表示为：
$$ \left\{ {\begin{split} &{\hat S\left( {{x_0}} \right) = {f^T}({x_0})\hat {\boldsymbol{\beta}} + {{\boldsymbol{r}}_0}^T{{\boldsymbol{R}}^{ - 1}}({\boldsymbol{Y}} - {\boldsymbol{F}}\hat {\boldsymbol{\beta }})} \\ & {{{\hat \sigma }^2}_{\hat S}({x_0}) = {{\hat \sigma }^2}\left( {1 + {{\boldsymbol{u}}^T}{{({{\boldsymbol{F}}^T}{{\boldsymbol{R}}^{ - 1}}{\boldsymbol{F}})}^{ - 1}}{\boldsymbol{u}} - {{\boldsymbol{r}}_0}^T{{\boldsymbol{R}}^{ - 1}}{{\boldsymbol{r}}_0}} \right)} \end{split}} \right. $$ (15) 其中，$ {{{\boldsymbol{u}} = }}{{{{\boldsymbol{F}}}}^T}{{\boldsymbol{R}}^{ - 1}}{{\boldsymbol{r}}_0} - {\boldsymbol{f}} $。
本文进行震陷可靠度分析时，式（10）—（15）中应用Kriging模型构建和预测其过程，采用MATLAB中的DACE工具箱实现。
2.2 黄土地基数值模型
采用FLAC3D有限差分软件建立黄土地基数值模型，模型尺寸设置为15 m×15 m×15 m，模型网格数为
3375 ，本构模型选择Mohr-Coulomb弹塑性本构模型。在静力分析时，底面和侧面选用固定边界，限制底面与侧面的位移和速度，顶部为自由边界。动力分析与静力分析不同，由于地震荷载会存在波的反射，因此在模型底面设置静态边界，侧面设置为自由场边界，模拟土体在实际中的状态（图1）。本文选用三条地震波分别是Kobe地震波、Imperial地震波和一条人工合成波。为方便后续说明，这里将选用的三条地震波分别命名为地震波1、地震波2及地震波3。地震波1的持续时间为25 s，时间间隔为0.02 s，最大加速度为0.345g，地震波2的持续时间为40 s，时间间隔为0.01 s，最大加速度为0.313g，地震波3的持续时间为20 s，时间间隔为0.02 s，最大加速度为0.153g。图2为经过滤波以及基线校正后所选地震波的时程曲线。
为了研究不同地震水平作用下震陷变形规律，将其改变幅值的大小来满足不同工况的需要，得到 0.1g、0.2g、0.3g、0.4g、0.5g、0.6g、0.7g不同峰值加速度大小的7种水平。其计算所得震陷量结果如表1所示。
表 1 不同地震波及不同峰值加速度作用下地基震陷量Table 1. Seismic subsidence of foundation under different seismic waves and peak accelerations.峰值加速度/g 震陷量/cm 地震波1 地震波2 地震波3 0.1 0.72 1.95 2.65 0.2 2.37 8.40 13.44 0.3 9.10 16.02 21.62 0.4 17.83 21.44 29.52 0.5 19.78 25.29 37.06 0.6 20.08 30.67 40.98 0.7 20.48 35.84 46.98 2.3 震陷变形影响因素敏感性分析
岩土体材料参数存在着变异性，但土体泊松比的变异系数非常小，在考虑土性参数不确定时可将其看作常量。孙军杰等[17]通过理论分析，给出了非饱和黄土动残余应变与黏聚力、内摩擦角、初始孔隙比、土层重度、土层埋深以及地震动荷载之间的定量关系式。压缩模量是体现土体压缩性的指标之一，作为土体的力学性质，在分析地基土体变形或沉降时起着重要作用，而土体的黏聚力和内摩擦角反映土体的强度特征，在静力分析中，黄土地基静力参数中密度对于计算结果的影响较明显。因此，这里选择密度、弹性模量、黏聚力及内摩擦角四种参数。采用FLAC3D结合灰色关联分析对影响黄土地基震陷变形的因素做敏感性分析，求得其密度、弹性模量、黏聚力及摩擦角四个参数的灰色关联度为$ q = [ {0.656\;8},\;{0.856\;2},\;{0.668\;5},\;{0.728\;1} ] $，敏感性排序为：弹性模量>内摩擦角>黏聚力>密度。
2.4 土性参数分布概率模型
本节选取密度（ρ）、压缩模量（Es）、黏聚力（c）及内摩擦角（φ）四种参数作为黄土震陷性评价的参数指标来进行分布概率模型研究。为了全面分析不同地貌单元4种土性参数的最优概率分布，选用可以包含大部分不确定性因素的概率分布形式包括正态分布、对数正态分布和威布尔分布进行假设检验。从而确定每个参数的最优概率分布形式[18]。
为获取原状黄土地基土性不同参数的分布概率模型，基于引汉济渭工程的渭河二级阶地地貌土体为例，通过对原状黄土的各种物理力学指标进行统计分析，得出各指标服从的概率密度函数及分布参数，图3所示为渭河二级阶地分布概率模型图，其中$ f\left( x \right) $表示概率密度函数。
![]()
图 3 不同参数的概率密度分布图Figure 3. Probability density distribution plots of different parameters由图3可知，从分布形态上来看，$ \rho $值的正态分布和对数正态分布整体较一致，两者均属于左偏态；其余三种土性参数正态分布、对数正态分布及威布尔分布三者分布较离散，差异性较大。
通过K-S检验法对4种土性参数的3种分布概率模型进行检验，求出样本值的理论累计概率分布与经验累计概率分布的最大差值（Dmax），与由显著性水平和样本数确定临界值（$ D_n^\alpha $）进行比较，计算结果如表2所示。四种参数均可接受正态分布、对数正态分布和威布尔分布。$ c $、$ {E_{\mathrm{s}}} $值的最优分布是正态分布，$ \varphi $、$ \rho $值的最优分布是威布尔分布，考虑到正态分布的优良性质，将正态分布作为4种土性参数的分布概率模型用于震陷可靠度计算。
表 2 分布假设检验结果Table 2. Distribution hypothesis test results检验参数 样本量 验证结果$ {D_{\max }} $ 可接受的临界值
$ D_n^\alpha /\left( {\alpha = 0.05} \right) $正态分布 对数正态分布 威布尔分布 结果 $ {D_{\max }} $ 结果 $ {D_{\max }} $ 结果 $ {D_{\max }} $ 内摩擦角 24 √ 0.180 √ 0.223 √ 0.093 0.273 黏聚力 24 √ 0.099 √ 0.125 √ 0.102 0.273 压缩模量 24 √ 0.094 √ 0.146 √ 0.164 0.273 密度 48 √ 0.150 √ 0.185 √ 0.115 0.196 2.5 基于Kriging代理模型的震陷可靠度计算方法
本节基于Kriging代理模型对地基震陷可靠度进行计算，这里进行
10000 次模拟，计算步骤如下：（1）根据前文统计出的土性参数（密度、压缩模量、黏聚力、摩擦角）的概率分布模型，确定地基土体参数的均值、标准差、分布类型等统计特性。
（2）FLAC3D6.0内置有Python编程语言，可以实现蒙特卡洛抽样与连续计算，利用Itasca开发的专门用于Python扩展编程的程序库，通过编程实现随机变量拉丁超立方抽样（LHS）、模型的建立以及计算，即会产生N组计算方案$ \left(\rho_1,E_{\mathrm{s}1},c_1,\varphi_1\right),\left(\rho_2,E_{\mathrm{s}2},c_2,\varphi_2\right),\cdots,(\rho_n,E_{\mathrm{s}n},c_n, \varphi_n) $，然后计算出对应的响应值。将计算模型文件保存为“n.f3sav”，后续模型按顺序编号，并将其作为源文件以便后续提取。
（3）对地震波设计不同的工况组合，计算每组工况下LHS的样本所对应的震陷量，并保存计算模型。
（4）利用Python编程语言从结果文件中批量提取竖向变形。
（5）采用MATLAB软件分别建立不同工况下的Kriging代理模型，以4种土体参数为输入，相应的地基震陷量为输出，对代理模型进行训练，得到满足精度要求的代理模型。经适当训练的代理模型能够较好地逼近实际情况，在此基础上可以十分方便地预测震陷值从而实现震陷可靠度的计算（图4）。
![]()
图 4 基于Kriging代理模型的震陷可靠度计算流程Figure 4. Calculation process of seismic subsidence reliability based on the Kriging surrogate model3. 算例分析
为验证本文提出方法的适用性，本节以引汉济渭工程为背景结合Kriging代理模型的震陷概率计算方法开展黄土地基震陷可靠度分析。
（1）最大可靠度
表3为不同地震波及不同地震峰值加速度作用下地基震陷的破坏概率，以渭河二级阶地为例。
表 3 不同地震波作用下地基震陷破坏概率Table 3. Probability of foundation subsidence failure under different seismic wave effects加速度/g 地震波1 地震波2 地震波3 0.1 0 0 0 0.2 0 0 0 0.3 0 0 0 0.4 0 0.072 0.116 0.5 0 0.17 0.378 0.6 0 0.232 0.704 0.7 0.002 0.264 0.888 由表3可知，在地震波1的作用下，该地基土体在地震波峰值加速度为0.7g时会出现破坏的概率，在地震波2和地震波3的作用下，在峰值加速度达到0.4g时会出现破坏的概率。三条地震波在峰值加速度达到最大时，其产生的破坏概率也有巨大差异，地震波1在峰值加速度为0.7g时破坏概率为0.002，地震波2在峰值加速度为0.7g时破坏概率为0.264，地震波3在峰值加速度为0.7g时破坏概率为0.888。
依据式（4）求得最大可靠度指标，图5为不同地震波作用下地基震陷的可靠度指标随峰值加速度的变化规律，最大可靠度指标的范围为−1.216～4.526。总体上可靠度指标随峰值加速度的增加呈非线性减小。但三条地震波的减小斜率并不相同，在地震波3作用下，可靠度指标随峰值加速度的变化斜率最大，说明在地震波3作用下，地基的可靠度受地震波峰值加速度的影响最大。对于已知地震波峰值加速度，可以快速粗略估计地基震陷的破坏概率，而不是单纯以震陷量来评价，这在风险评估中具有更为重要的意义。
![]()
图 5 可靠度分析获得的地基震陷最大可靠度Figure 5. Maximum reliability index of foundation seismic subsidence obtained from reliability analysis（2）最小可靠度
表4为不同地震波及不同地震峰值加速度作用下地基震陷的破坏概率，以渭河二级阶地为例。由表4可知，在地震波1的作用下，该地基土体在地震波峰值加速度为0.1g～0.7g时均会出现完好概率，在地震波2和地震波3的作用下，在峰值加速度分别达到0.4g及以后和0.3g及以后完好概率均为0。
表 4 不同地震波作用下地基震陷完好概率Table 4. Probability of intact seismic subsidence of foundation under different seismic wave effects加速度/g 地震波1 地震波2 地震波3 0.1 0.946 0.854 0.842 0.2 0.392 0.094 0.832 0.3 0.238 0.004 0 0.4 0.01 0 0 0.5 0.018 0 0 0.6 0.012 0 0 0.7 0.002 0 0 依据式（8）求得最小可靠度指标，图6为在不同地震波作用下地基震陷的最小可靠度随峰值加速度的变化规律，最小可靠度指标的变化范围为−2.878～1.607。从整体来说，随着地震峰值加速度的增大，地基在地震作用下的最小可靠度指标逐渐降低。当地震峰值加速度为0.1g时，震陷最小可靠度较高，都为正值；当地震峰值加速度为0.2g时，地震最小可靠度显著减小，且超过0.2g以后最小可靠度均为负值。
![]()
图 6 可靠度分析获得的地基震陷的最小可靠度指标Figure 6. Minimum reliability index of foundation seismic subsidence obtained from reliability analysis（3）变异系数对震陷可靠度的影响
为了更好地分析随机变量的变异性大小对震陷可靠度的影响，本文计算了各变量在不同变异系数组合情况下，四种土体参数变异系数随地基震陷可靠度的变化情况，工况组合见表5。
表 5 各参数变异系数工况组合表Table 5. Combination table of variation coefficient for each parameter工况 COV 密度 弹性模量 黏聚力 摩擦角 1-1 0.01 0.3 0.2 0.3 1-2 0.05 1-3 0.1 1-4 0.15 1-5 0.2 2-1 0.05 0.05 0.2 0.3 2-2 0.1 2-3 0.2 2-4 0.3 2-5 0.4 3-1 0.05 0.3 0.05 0.3 3-2 0.1 3-3 0.2 3-4 0.3 3-5 0.4 4-1 0.05 0.3 0.2 0.1 4-2 0.2 4-3 0.3 4-4 0.4 4-5 0.5 计算结果如图7所示。由图可知，随各参数变异系数的增加，震陷最大可靠度逐渐减小，而最小可靠度逐渐增大。当$ COV(\rho) $从0.01增加至0.2，相应的$ {\beta _{\text{d}}} $从3.72减小至3.05，最小可靠度（$ {\beta _{\text{h}}} $）从−1.72增加至−1.55，降幅为21.97%，增幅为10.96%；当$ COV(E_{\mathrm{s}}) $从0.05增加至0.4，相应的$ {\beta _{\text{d}}} $从3.89降至3.29，$ {\beta _{\text{h}}} $从−1.89增加至−1.64，降幅为18.24%，增幅为15.24%；当$ COV(c) $从0.05增加至0.4，$ {\beta _{\text{d}}} $从4.26降至2.89，$ {\beta _{\text{h}}} $从−1.81增加至−1.60，降幅为47.40%，增幅为13.13%；当$ COV(\varphi)$从0.1增加至0.5，$ {\beta _{\text{d}}} $从3.72降至2.74，$ {\beta _{\text{h}}} $从−1.99增加至−1.63，降幅为35.77%，增幅为22.09%。对比数据，在同样的增幅下，最大可靠度的变化幅度比最小可靠度的变化幅度大说明最大可靠度对变异系数更为敏感。计算各个参数最大可靠度起末两点斜率的绝对值，分别为3.526、1.714、3.914和2.45，可看出黏聚力变异系数对震陷最大可靠度影响更为显著。
![]()
图 7 不同参数变异系数对震陷可靠度的影响规律Figure 7. The influence of different parameter coefficient of variations on seismic subsidence reliability4. 结论
（1）Kriging代理模型可以在小样本抽样的情况下得到较好的近似拟合效果，达到精度要求，提高了震陷可靠度的计算效率。
（2）采用震陷可靠度方法来评价地基土体的震陷性，能够合理地考虑土性参数的变异性，更加符合实际情况，具有更好的可靠性和适用性，对于已知地震波峰值加速度，可以快速粗略估计地基震陷的破坏概率，而不是单纯的以震陷量来评价，这在风险评估中具有更为重要的意义。
（3）综合4种土体参数的变异系数对震陷可靠度的影响可以发现，最大可靠度对各个参数的变异系数更为敏感，此外四种土体参数中黏聚力的变异系数对震陷最大可靠度的影响更为显著。
-
![]()
图 2 扎哈淖尔露天矿北帮研究剖面位置
Figure 2. Study cross-section at the north slope at Zhahanaoer open-pit mine
![]()
图 3 扎哈淖尔露天矿北帮地质剖面
Figure 3. Geological cross-section of the north slope of open-pit mine
![]()
图 4 扎哈淖尔露天矿北帮弱层岩芯
Figure 4. Core samples of weak layers on the northern slope of open-pit mine
![]()
图 7 强度折减弱化北帮边坡潜在滑移面模拟结果
Figure 7. SRM modelled potential slip surface of the northern slope
表 1 连续型指标影响等级划分
Table 1 Classification of impact levels for continuous influencing indicators
稳定性 坡高/m 坡度/（°） 年均降雨量/mm 地表变形
速率/（mm·d−1）稳定 0～100 0～15 0～500 5 基本稳定 >100～200 >15～30 >500～800 >5～30 欠稳定 >200～300 >30～50 >800～1200 >30～80 不稳定 >300 >50 >1200 >80 
下载: 导出CSV
表 2 离散型指标影响等级划分
Table 2 Classification of impact levels for discrete influencing indicators
稳定性 岩性 结构类型 弱层 地面变形 地下水影响 稳定 坚硬岩体 均质/反倾 无 无 很弱 基本稳定 中等坚硬 斜交/横坡 反倾夹层 弱 较弱 欠稳定 软弱岩体 近水平坡 顺倾夹层、
反倾基岩中等 较强 不稳定 松散体 顺向坡 顺倾基岩 强烈 很强
下载: 导出CSV
表 3 层次分析法（AHP）影响因子标度
Table 3 Analytic hierarchy process (AHP) influence factor scale
标度 含义 1 ${u_i}$和${u_j}$指标影响程度相同 3 ${u_i}$和${u_j}$指标影响程度相比，一个比另一个稍微重要 5 ${u_i}$和${u_j}$指标影响程度相比，一个比另一个明显重要 7 ${u_i}$和${u_j}$指标影响程度相比，一个比另一个强烈重要 9 ${u_i}$和${u_j}$指标影响程度相比，一个比另一个极端重要 2,4,6,8 介于以上两种比较之间的标度值 倒数 ${u_i}$和${u_j}$指标之间判断${b_{ij}}$，${u_j}$和${u_i}$指标之间判断${1 \mathord{\left/ {\vphantom {1 {{b_{ij}}}}} \right. } {{b_{ij}}}}$
下载: 导出CSV
表 4 离散型指标评价隶属度表
Table 4 Discrete index evaluation membership degree
离散型指标 具体指标 离散型指标评价隶属度 稳定 基本稳定 欠稳定 不稳定 岩性 坚硬岩体 0.8 0.2 0 0 中等坚硬 0.4 0.5 0.1 0 软弱岩体 0 0.2 0.5 0.3 松散体 0 0 0.2 0.8 结构类型 顺向坡 0 0 0.2 0.8 近水平坡 0.1 0.2 0.7 0 斜交/横坡 0.2 0.7 0.1 0 均质/反倾 0.8 0.2 0 0 弱层 无 1 0 0 0 反倾夹层 0.2 0.7 0.1 0 顺倾夹层、反倾基岩 0 0.1 0.7 0.2 顺倾基岩 0 0 0.2 0.8 地面变形 无 0.8 0.2 0 0 弱 0.2 0.7 0.1 0 中等 0 0.1 0.7 0.2 强烈 0 0 0.2 0.8 地下水影响 很弱 0.55 0.30 0.10 0.05 较弱 0.25 0.50 0.15 0.10 较强 0.05 0.10 0.30 0.55 很强 0.05 0.15 0.10 0.70
下载: 导出CSV
表 5 北帮边坡定量指标隶属度
Table 5 Membership degree of quantitative indexes for the northern slope
稳定性 坡高隶属度 坡度隶属度 年均降雨量
隶属度地表变形速率
隶属度稳定 0 0.86 1 0 基本稳定 0.16 0.14 0 0.83 欠稳定 0.84 0 0 0.17 不稳定 0 0 0 0
下载: 导出CSV
表 6 北帮边坡定性指标隶属度
Table 6 Membership degrees of qualitative indexes for the northern slope
稳定性 岩性隶属度 结构类型
隶属度弱层隶属度 地面变形
隶属度地下水影响
隶属度稳定 0 0.80 0.20 0 0.05 基本稳定 0.20 0.20 0.70 0 0.10 欠稳定 0.50 0 0.10 0.20 0.30 不稳定 0.30 0 0 0.80 0.55
下载: 导出CSV
表 7 岩层物理力学参数表
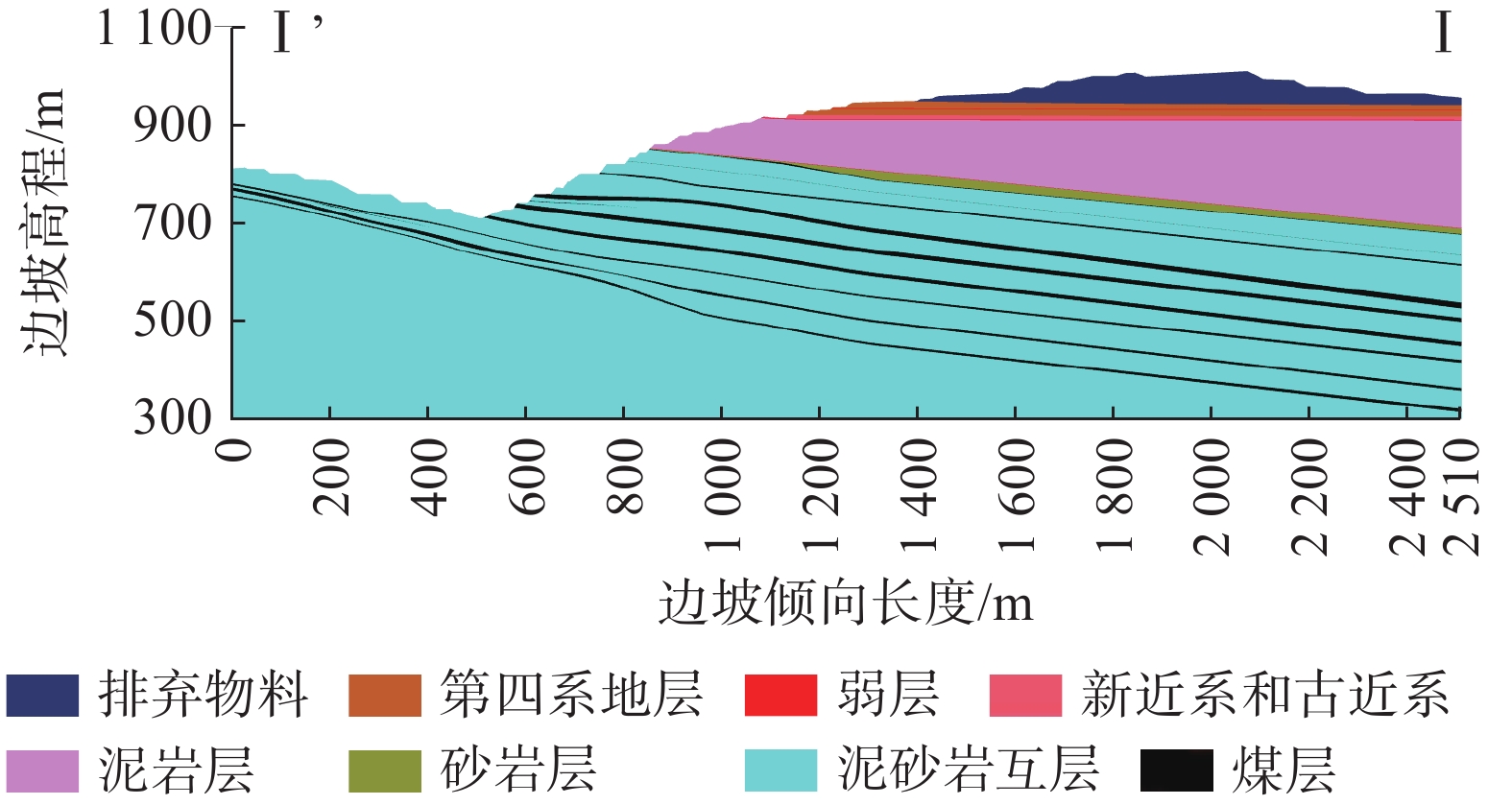
Table 7 Physico-mechanical parameters of strata
岩层 重度/（kN·m−3） 黏聚力/kPa 内摩擦角/（°） 排弃物料 17.70 10.0 20.0 第四系地层 17.90 17.0 11.7 弱层 17.90 8.0 5.7 新近系和古近系地层 17.90 14.0 13.0 泥岩层 20.20 33.7 15.4 砂岩层 24.40 40.0 28.0 泥砂岩互层 23.45 35.0 24.6 煤层 12.70 24.5 21.0
下载: 导出CSV
表 8 边坡稳定性状态划分
Table 8 Classification of slope stability states
边坡安全系数 F<1.00 1.00≤F<1.05 1.05≤F<1.20 F≥1.20 边坡稳定状态 不稳定 欠稳定 基本稳定 稳定
下载: 导出CSV
-
[1] 李浩荡,佘长超,周永利,等. 我国露天煤矿开采技术综述及展望[J]. 煤炭科学技术,2019,47(10):24 − 35. [LI Haodang,SHE Changchao,ZHOU Yongli,et al. Summary and prospect of open-pit coal mining technology in China[J]. Coal Science and Technology,2019,47(10):24 − 35. (in Chinese with English abstract)] LI Haodang, SHE Changchao, ZHOU Yongli, et al . Summary and prospect of open-pit coal mining technology in China［J］. Coal Science and Technology,2019 ,47 （10 ）:24 −35 . （in Chinese with English abstract）[2] WEI Zuoan,YIN Guangzhi,WAN Ling,et al. Case history of controlling a landslide at Panluo open-pit mine in China[J]. Environmental Geology,2008,54(4):699 − 709. DOI: 10.1007/s00254-007-0839-y
[3] 谭文辉,乔兰,王鹏. 高陡边坡岩体力学环境的模糊综合评判研究[J]. 金属矿山,2002(12):20 − 22. [TAN Wenhui,QIAO Lan,WANG Peng. Study on the fuzzy comprehensive evaluation of the mechanical environment of rockmass in high-steep slopes[J]. Metal Mine,2002(12):20 − 22. (in Chinese with English abstract)] DOI: 10.3321/j.issn:1001-1250.2002.12.007 TAN Wenhui, QIAO Lan, WANG Peng . Study on the fuzzy comprehensive evaluation of the mechanical environment of rockmass in high-steep slopes［J］. Metal Mine,2002 （12 ）:20 −22 . （in Chinese with English abstract） DOI: 10.3321/j.issn:1001-1250.2002.12.007[4] 张永杰,邓俊强,李侑军,等. 考虑隶属函数特性的边坡模糊可靠性分析[J]. 岩土工程学报,2018,40(7):1350 − 1358. [ZHANG Yongjie,DENG Junqiang,LI Youjun,et al. Fuzzy reliability analysis of slopes considering characteristics of membership function[J]. Chinese Journal of Geotechnical Engineering,2018,40(7):1350 − 1358. (in Chinese with English abstract)] ZHANG Yongjie, DENG Junqiang, LI Youjun, et al . Fuzzy reliability analysis of slopes considering characteristics of membership function［J］. Chinese Journal of Geotechnical Engineering,2018 ,40 （7 ）:1350 −1358 . （in Chinese with English abstract）[5] 蒋中明. 模糊分析理论及其岩土工程中的应用研究[J]. 岩石力学与工程学报,2004,23(24):4263. [JIANG Zhongming. Study on fuzzy analysis theory and its application in geotechnical engineering[J]. Chinese Journal of Rock Mechanics and Engineering,2004,23(24):4263. (in Chinese with English abstract)] JIANG Zhongming . Study on fuzzy analysis theory and its application in geotechnical engineering［J］. Chinese Journal of Rock Mechanics and Engineering,2004 ,23 （24 ）:4263 . （in Chinese with English abstract）[6] 杨正荣,喜文飞,史正涛,等. 基于SBAS-InSAR技术的白鹤滩水电站库岸潜在滑坡变形分析[J]. 中国地质灾害与防治学报,2022,33(5):83 − 92. [YANG Zhengrong,XI Wenfei,SHI Zhengtao,et al. Deformation analysis in the bank slopes in the reservoir area of Baihetan Hydropower Station based on SBAS-InSAR technology[J]. The Chinese Journal of Geological Hazard and Control,2022,33(5):83 − 92. (in Chinese with English abstract)] YANG Zhengrong, XI Wenfei, SHI Zhengtao, et al. Deformation analysis in the bank slopes in the reservoir area of Baihetan Hydropower Station based on SBAS-InSAR technology［J］. The Chinese Journal of Geological Hazard and Control, 2022, 33（5）: 83 − 92. （in Chinese with English abstract）
[7] 廖小平, 徐风光, 蔡旭东, 等. 香丽高速公路边坡地质灾害发育特征与易发性区划[J]. 中国地质灾害与防治学报,2021,32(5):121 − 129. [LIAO Xiaoping, XU Fengguang, CAI Xudong,etal. Development characteristics and susceptibality zoning of slope geological hazards in Xiangli expressway[J]. The Chinese Journal of Geological Hazard and Control,2021,32(5):121 − 129. (in Chinese with English abstract)] LIAO Xiaoping, XU Fengguang, CAI Xudong, etal . Development characteristics and susceptibality zoning of slope geological hazards in Xiangli expressway［J］. The Chinese Journal of Geological Hazard and Control,2021 ,32 （5 ）:121 −129 . （in Chinese with English abstract）[8] 刘春. 运用AHP-FUZZY法判定岩质边坡稳定性[J]. 华侨大学学报(自然科学版),2006,27(4):388 − 391. [LIU Chun. Slope stability analysis by AHP-FUZZY method[J]. Journal of Huaqiao University (Natural Science),2006,27(4):388 − 391. (in Chinese with English abstract)] LIU Chun . Slope stability analysis by AHP-FUZZY method［J］. Journal of Huaqiao University （Natural Science）,2006 ,27 （4 ）:388 −391 . （in Chinese with English abstract）[9] 胡田飞,朱本珍. 基于熵权法和层次分析法的复杂边坡稳定性模糊综合评价方法[J]. 铁道建筑,2013,53(12):69 − 73. [HU Tianfei,ZHU Benzhen. Fuzzy comprehensive evaluation method of complex slope stability based on entropy weight method and analytic hierarchy process[J]. Railway Engineering,2013,53(12):69 − 73. (in Chinese)] HU Tianfei, ZHU Benzhen . Fuzzy comprehensive evaluation method of complex slope stability based on entropy weight method and analytic hierarchy process［J］. Railway Engineering,2013 ,53 （12 ）:69 −73 . （in Chinese）[10] 张紫杉,王述红,王斐笠. 基于空间块体表征的岩质边坡稳定性综合评价[J]. 东北大学学报(自然科学版),2018,39(6):896 − 901. [ZHANG Zishan,WANG Shuhong,WANG Feili. Comprehensive assessment of rock slope stability based on spatial block identification[J]. Journal of Northeastern University (Natural Science),2018,39(6):896 − 901. (in Chinese with English abstract)] ZHANG Zishan, WANG Shuhong, WANG Feili . Comprehensive assessment of rock slope stability based on spatial block identification［J］. Journal of Northeastern University （Natural Science）,2018 ,39 （6 ）:896 −901 . （in Chinese with English abstract）[11] 张勇慧,李红旭,盛谦,等. 基于模糊综合评判的公路岩质边坡稳定性分级研究[J]. 岩土力学,2010,31(10):3151 − 3156. [ZHANG Yonghui,LI Hongxu,SHENG Qian,et al. Study of stability gradation of highway rock slopes based on fuzzy comprehensive evaluation[J]. Rock and Soil Mechanics,2010,31(10):3151 − 3156. (in Chinese with English abstract)] ZHANG Yonghui, LI Hongxu, SHENG Qian, et al . Study of stability gradation of highway rock slopes based on fuzzy comprehensive evaluation［J］. Rock and Soil Mechanics,2010 ,31 （10 ）:3151 −3156 . （in Chinese with English abstract）[12] 中华人民共和国住房和城乡建设部. 煤炭工业露天矿边坡工程设计标准:GB51289—2018[S]. 北京:中国计划出版社:2018. [Ministry of Housing and Urban-Rural Development of the People's Republic of China. Standard for design of slope engineering of open pit mine of coal industry:GB51289—2018[S]. Beijing:China Planning Press:2018. (in Chinese)] Ministry of Housing and Urban-Rural Development of the People's Republic of China. Standard for design of slope engineering of open pit mine of coal industry: GB51289—2018［S］. Beijing: China Planning Press: 2018. （in Chinese）
[13] 孙书伟,朱本珍,马惠民. 一种基于模糊理论的区域性高边坡稳定性评价方法[J]. 铁道学报,2010,32(3):77 − 83. [SUN Shuwei,ZHU Benzhen,MA Huimin. Method based on fuzzy theory for evaluation of regional high slopes stability[J]. Journal of the China Railway Society,2010,32(3):77 − 83. (in Chinese with English abstract)] DOI: 10.3969/j.issn.1001-8360.2010.03.014 SUN Shuwei, ZHU Benzhen, MA Huimin . Method based on fuzzy theory for evaluation of regional high slopes stability［J］. Journal of the China Railway Society,2010 ,32 （3 ）:77 −83 . （in Chinese with English abstract） DOI: 10.3969/j.issn.1001-8360.2010.03.014[14] CHEN Wei,LI Wenping,CHAI Huichan,et al. GIS-based landslide susceptibility mapping using analytical hierarchy process (AHP) and certainty factor (CF) models for the Baozhong region of Baoji City,China[J]. Environmental Earth Sciences,2016,75(1):63. DOI: 10.1007/s12665-015-4795-7
[15] 张卜平, 朱兴华, 成玉祥,等. 黄土潜蚀机理及其致灾效应研究综述[J]. 中国地质灾害与防治学报,2021,32(6):41 − 52. [ZHANG Buping, ZHU Xinghua, CHENG Yuxiang, etal. A review on loess subsurface-erosion mechanism and it’s hazard effects[J]. The Chinese Journal of Geological Hazard and Control,2021,32(6):41 − 52. (in Chinese with English abstract)] ZHANG Buping, ZHU Xinghua, CHENG Yuxiang, etal . A review on loess subsurface-erosion mechanism and it’s hazard effects［J］. The Chinese Journal of Geological Hazard and Control,2021 ,32 （6 ）:41 −52 . （in Chinese with English abstract）[16] 谢全敏,夏元友. 岩体边坡治理决策的模糊层次分析方法研究[J]. 岩石力学与工程学报,2003,22(7):1117 − 1120. [XIE Quanmin,XIA Yuanyou. Fuzzy hierarchy analysis on decision making of rockmass slope treatment based on entropy weight[J]. Chinese Journal of Rock Mechanics and Engineering,2003,22(7):1117 − 1120. (in Chinese with English abstract)] XIE Quanmin, XIA Yuanyou . Fuzzy hierarchy analysis on decision making of rockmass slope treatment based on entropy weight［J］. Chinese Journal of Rock Mechanics and Engineering,2003 ,22 （7 ）:1117 −1120 . （in Chinese with English abstract）[17] 徐卫亚,蒋中明,石安池. 基于模糊集理论的边坡稳定性分析[J]. 岩土工程学报,2003,25(4):409 − 413. [XU Weiya,JIANG Zhongming,SHI Anchi. Slope stability analysis using fuzzy sets theory[J]. Chinese Journal of Geotechnical Engineering,2003,25(4):409 − 413. (in Chinese with English abstract)] XU Weiya, JIANG Zhongming, SHI Anchi . Slope stability analysis using fuzzy sets theory［J］. Chinese Journal of Geotechnical Engineering,2003 ,25 （4 ）:409 −413 . （in Chinese with English abstract）[18] 牛昴懿,杨春风. 锚固路堑高边坡稳定性非线性模糊评判[J]. 公路交通技术,2015,31(2):13 − 19. [NIU Maoyi,YANG Chunfeng. Nonlinear fuzzy evaluation for stability of high cut slopes after anchorage[J]. Technology of Highway and Transport,2015,31(2):13 − 19. (in Chinese with English abstract)] NIU Maoyi, YANG Chunfeng . Nonlinear fuzzy evaluation for stability of high cut slopes after anchorage［J］. Technology of Highway and Transport,2015 ,31 （2 ）:13 −19 . （in Chinese with English abstract）[19] SUN Wenbin,XUE Yanchao. An improved fuzzy comprehensive evaluation system and application for risk assessment of floor water inrush in deep mining[J]. Geotechnical and Geological Engineering,2019,37(3):1135 − 1145. DOI: 10.1007/s10706-018-0673-x
[20] 徐勇超,李苗苗. 扎哈淖尔露天矿北帮边坡稳定性研究[J]. 露天采矿技术,2020,35(2):14 − 18. [XU Yongchao,LI Miaomiao. Study on stability of north slope of Zhahanao'er open-pit mine[J]. Opencast Mining Technology,2020,35(2):14 − 18. (in Chinese with English abstract)] XU Yongchao, LI Miaomiao . Study on stability of north slope of Zhahanao'er open-pit mine［J］. Opencast Mining Technology,2020 ,35 （2 ）:14 −18 . （in Chinese with English abstract）[21] 靳鹏,申力,韩晓极,等. 辽宁抚顺西露天矿地质灾害时空分布特征及影响因素分析[J]. 中国地质灾害与防治学报,2022,33(3):68 − 76. [JIN Peng,SHEN Li,HAN Xiaoji,et al. Spatial-temporal distribution characteristics and influencing factors of geological disasters in the open-pit mining area of western Fushun,Liaoning Province[J]. The Chinese Journal of Geological Hazard and Control,2022,33(3):68 − 76. (in Chinese with English abstract)] JIN Peng, SHEN Li, HAN Xiaoji, et al. Spatial-temporal distribution characteristics and influencing factors of geological disasters in the open-pit mining area of western Fushun,Liaoning Province［J］. The Chinese Journal of Geological Hazard and Control, 2022, 33（3）: 68 − 76. （in Chinese with English abstract）
[22] 付玉宁. 边坡形态与岩层产状对反倾向边坡稳定性影响的数值分析[D]. 西安:长安大学,2015. [FU Yuning. Numerical analysis of the influence of slope shape and rock occurrence on the stability of anti-dip slope[D]. Xi’an:Changan University,2015. (in Chinese with English abstract)] FU Yuning. Numerical analysis of the influence of slope shape and rock occurrence on the stability of anti-dip slope［D］. Xi’an: Changan University, 2015. （in Chinese with English abstract）
[23] 梁乃森,钱程,穆文平,等. 大牛地气田区地下水水质模糊综合评价[J]. 水文地质工程地质,2020,47(3):52 − 59. [LIANG Naisen,QIAN Cheng,MU Wenping,et al. Fuzzy comprehensive evaluation of groundwater quality of the Daniudi gas field area[J]. Hydrogeology & Engineering Geology,2020,47(3):52 − 59. (in Chinese with English abstract)] LIANG Naisen, QIAN Cheng, MU Wenping, et al . Fuzzy comprehensive evaluation of groundwater quality of the Daniudi gas field area［J］. Hydrogeology & Engineering Geology,2020 ,47 （3 ）:52 −59 . （in Chinese with English abstract）[24] 朱小飞,王永君,李大军. 模糊评价中最大隶属度原则有效性检验[J]. 测绘与空间地理信息,2016,39(5):135 − 137. [ZHU Xiaofei,WANG Yongjun,LI Dajun. The effectiveness test of the maximum membership principle in fuzzy comprehensive evaluation[J]. Geomatics & Spatial Information Technology,2016,39(5):135 − 137. (in Chinese with English abstract)] DOI: 10.3969/j.issn.1672-5867.2016.05.039 ZHU Xiaofei, WANG Yongjun, LI Dajun . The effectiveness test of the maximum membership principle in fuzzy comprehensive evaluation［J］. Geomatics & Spatial Information Technology,2016 ,39 （5 ）:135 −137 . （in Chinese with English abstract） DOI: 10.3969/j.issn.1672-5867.2016.05.039[25] 陈亮,邬长福,陈祖云,等. 基于AHP-模糊综合评价法的非煤露天矿山安全标准化复评体系研究[J]. 矿业研究与开发,2016,36(4):99 − 103. [CHEN Liang,WU Changfu,CHEN Zuyun,et al. Study on the reevaluation system of non-coal open-pit mine safety standardization by AHP-fuzzy comprehensive evaluation method[J]. Mining Research and Development,2016,36(4):99 − 103. (in Chinese with English abstract)] CHEN Liang, WU Changfu, CHEN Zuyun, et al . Study on the reevaluation system of non-coal open-pit mine safety standardization by AHP-fuzzy comprehensive evaluation method［J］. Mining Research and Development,2016 ,36 （4 ）:99 −103 . （in Chinese with English abstract）[26] ZHANG Fei,YANG Tianhong,LI Lianchong,et al. Cooperative monitoring and numerical investigation on the stability of the south slope of the Fushun west open-pit mine[J]. Bulletin of Engineering Geology and the Environment,2019,78(4):2409 − 2429. DOI: 10.1007/s10064-018-1248-z
[27] LI Yuchao,CHEN Jianping,ZHOU Fujun,et al. Stability evaluation of rock slope based on discrete fracture network and discrete element model:A case study for the right bank of Yigong Zangbu Bridge[J]. Acta Geotechnica,2022,17(4):1423 − 1441. DOI: 10.1007/s11440-021-01369-5
[28] 杨建成,邓琴. 基于局部强度折减法的多级边坡潜在滑动面分析[J]. 公路,2016,61(12):19 − 23. [YANG Jiancheng,DENG Qin. Analysis of multi-stage slope potential sliding surface based on local strength reduction method[J]. Highway,2016,61(12):19 − 23. (in Chinese with English abstract)] YANG Jiancheng, DENG Qin . Analysis of multi-stage slope potential sliding surface based on local strength reduction method［J］. Highway,2016 ,61 （12 ）:19 −23 . （in Chinese with English abstract）[29] 侯世伟,马士贺,李宏男,等. 基于局部强度阶梯折减法的边坡渐进破坏研究[J]. 防灾减灾工程学报,2020,40(1):72 − 78. [HOU Shiwei,MA Shihe,LI Hongnan,et al. Research on progressive slope failure based on stepwise reduction method of local strength[J]. Journal of Disaster Prevention and Mitigation Engineering,2020,40(1):72 − 78. (in Chinese with English abstract)] HOU Shiwei, MA Shihe, LI Hongnan, et al . Research on progressive slope failure based on stepwise reduction method of local strength［J］. Journal of Disaster Prevention and Mitigation Engineering,2020 ,40 （1 ）:72 −78 . （in Chinese with English abstract）
计量
- 文章访问数: 222
- HTML全文浏览量: 65
- PDF下载量: 120
邮件订阅
RSS