Analysis of the rainfall threshold for post-fire debris flow initiation: A case study of the debris flow at Ren’eyong gully in Xiangcheng County, Sichuan Province
-
摘要:
2014年6月1日，中国西南中横断山区仁额拥沟遭受了一次森林大火，火后的短时低雨强降雨在3#支沟内激发了3次泥石流；2015年8月的一次强降雨在仁额拥沟的1#、2#和3#支沟及其他附近的多个更小的流域内均激发了泥石流。为了解火后泥石流的降雨响应特征，文章采用距离修正的方式处理降雨数据，对4次泥石流进行降雨过程分析，查明了流域特征对泥石流启动的作用及其对各支沟泥石流不同降雨阈值的影响。研究发现：（1）泥石流降雨阈值在火后非常低且有随时间推移而增大的趋势；（2）仁额拥沟火后泥石流具有高频率特征，其原因除了在火后天然植被的破坏后降雨对坡面径流和侵蚀效应的放大，流域本身的性质也有极大的贡献；（3）各支沟内泥石流降雨阈值差异的主要原因在于流域面积的差异，泥石流侵蚀受制于径流量大小。
Abstract:In the early summer of 2014, a wildfire ravaged the Ren’eyong valley in the central Mt. Hengduan region of southwestern China. Following the blaze, debris flows were triggered three times in branch No. 3 due to short-term, low intensity rainfall. A year later, in August 2015, a brief period of high-intensity rainfall generated debris flows not only in branch No.3, but also in branch No. 1 and No. 2, as well as several smaller basins in the vicinity. To investigate the rainfall response characteristics of post-wildfire debris flow, the distance correction method was used to process the rainfall data. By analyzing the rainfall patterns of four debris flow events, the reseachers were able to identify the effects of watershed characteristics on the initiation of debris flow and its influence on different rainfall thresholds in each branch. The study found that: 1） Post fire debris flows can occur at a low rainfall threshold, which tends to increase over time. 2） The Ren’eyong valley experience high-frequency post fire debris flows, which can be attributed not only to the amplification of slope runoff and erosion caused by rainfall after the destruction of natural vegetation due to the wildfire, but also to the geological and geomorphic conditions of the area. 3） The rainfall threshold in each branch is primarily dependent on the drainage area, as the magnitude of discharge controls the entrainment.
-
0. 引言
地基稳定性受多种因素影响[1 − 2]，特别是黄土地区，受震陷影响很大。黄土震陷作为一种严重的地质灾害，一旦发生将会造成非常严重的后果。前人对与黄土震陷的研究基本是以动三轴试验为主，以单个震陷量作为震陷性的主要的评价指标[3 − 6]。然而黄土地基震陷的准确性评价受到土性参数不确定性的影响，其中物理力学指标的概率分布类型和变异性会对评价结果产生影响。针对岩土工程中参数、计算模型、荷载等不确定性问题，其主要的不确定性分析方法包括：概率分析方法[7]、随机有限元法[8]、灰色系统评价法[9]、模糊数学法[10]、神经网络评价方法[11]等。这些不确定性方法可以考虑得更加全面，从而提高评价结果的准确性，使结果更为科学合理。
关于黄土震陷在不确定性方面的研究，李波等[12]采用灰色关联方法和逐步判别方法建立了耦合式软土震陷判别模型从而实现软土震陷等级的判定。在黄土震陷概率评价方面，谭芳[13]将概率地震危险性分析方法引入震陷计算中，采用不确定性分析方法分析了黄土震陷与地震参数之间的关系，从而提出一种考虑地震随机性的黄土震陷预测方法。任森等[14]基于大量动三轴试验，结合场地地震危险性概率分析方法，确定了研究区内的震陷区划。孙军杰等[15]依据残余应变估算模型采用概率统计等非确定性分析方法对地基动力沉降进行了概率分析。可见概率分析方法在土体动力沉降中已经得到了初步研究。
然而到目前为止，还没有研究将可靠度理论应用于黄土地基震陷的分析中。因此本文尝试将可靠度理论应用于黄土地基震陷评价中，使用可靠度方法对黄土地基震陷性进行分析。可靠度方法和传统的确定性分析方法相互补充与结合，有助于进行震陷可靠度分析。
1. 黄土地基震陷可靠度指标
可靠度理论在边坡稳定分析中被广泛应用，而边坡工程的不确定因素主要为土体参数的抗剪强度（内摩擦角、黏聚力）[16 − 18]。其依托蒙特卡洛分析法通过计算出多组安全系数值将小于1的安全系数的次数与计算次数的比值称作失效概率。因此可求得对应的可靠度指标（$ \mathrm{\beta } $）为：
$$ \beta ={\varPhi }^{-1}(1-{P}_{\text{f}}) $$ (1) 式中：$ \varPhi $——标准正态分布的累计分布函数；
${P_{\text{f}}}$——失效概率。
在目前已有的地震灾害评估中，尚未有关于地基震陷量的标准划分依据。根据中国地震局发布的《震害调查及地震损失评定工作指南》，可以采用“地基基础破坏等级标准”来评估震陷灾害的程度[16]，将震陷量小于2 cm的定义为基本完好，震陷量大于40 cm的定义为破坏。
参考可靠度理论在边坡稳定性评价中的应用，结合黄土动力学对震陷等级的划分，本文提出了一种对黄土地基震陷评价的可靠度指标。
（1）最大可靠度
在震陷等级划分中将震陷量大于40 cm的定义为震陷破坏，因此可采用破坏概率（Pd）来判定其震陷破坏状态，即$ {P_{\mathrm{d}}} = P\left( {S \geqslant 40} \right) $。将$ \beta_{\mathrm{d}} $定义为：
$$ {\beta _{\mathrm{d}}} = \frac{{40 - {u_{\mathrm{s}}}}}{{{\sigma _{\mathrm{s}}}}} $$ (2) 式中：$ {u_{\mathrm{s}}} $——震陷量的平均值；
$ {\sigma _{\mathrm{s}}} $——震陷量的标准差。
如果震陷量符合标准正态分布，破坏概率与可靠度的关系可表示为：
$$ {P_{\mathrm{d}}} = P\left( {S > 40} \right) = 1 - \varPhi \left(\frac{{40 - {u_{\mathrm{s}}}}}{{{\sigma _{\mathrm{s}}}}}\right) = 1 - \varPhi ({\beta _{\mathrm{d}}}) $$ (3) 则根据可靠度理论，将破坏概率对应的可靠度称为最大可靠度（${\beta }_{\text{d}} $），也就是指衡量地基震陷最大安全程度的标准，其计算公式为：
$$ {\beta }_{\text{d}}={\varPhi }^{-1}(1-{P}_{\text{d}}) $$ (4) 根据蒙特卡罗可靠度计算方法可定义破坏概率为：
$$ {P_{\text{d}}} = \frac{M}{N} $$ (5) 式中：$ {P}_{{\mathrm{d}}} $——地基震陷破坏概率；
M——抽样次数中震陷量大于40 cm的次数；
N——蒙特卡洛分析法总的抽样次数。
（2）最小可靠度
在震陷等级划分中将震陷量小于2 cm的定义为基本完好，因此可采用完好概率（Ph）来判定其完好状态，即$ {P_{\mathrm{h}}} = P\left( {S \leqslant 2} \right) $。将$ {\beta _{\mathrm{h}}} $定义为：
$$ {\beta _{\mathrm{h}}} = \frac{{2 - {u_{\mathrm{s}}}}}{{{\sigma _{\mathrm{s}}}}} $$ (6) 式中：$ {u_{\mathrm{s}}} $——震陷量的平均值；
$ {\sigma _{\mathrm{s}}} $——震陷量的标准差。
如果震陷量符合标准正态分布，完好概率（Ph）与可靠度的关系可表示为：
$$ {P_{\mathrm{h}}} = P\left( {S < 2} \right) = \varPhi \left(\frac{{2 - {u_{\mathrm{s}}}}}{{{\sigma _{\mathrm{s}}}}}\right) = \varPhi ({\beta _{\mathrm{h}}}) $$ (7) 根据可靠度理论，将完好概率对应的可靠度称为最小可靠度（${\beta _{\mathrm{h}}} $），也就是指衡量地基震陷完好程度的标准，其计算公式为：
$$ {\beta _{\text{h}}} = {\varPhi ^{ - 1}}\left( {{P_{\text{h}}}} \right) $$ (8) 根据蒙特卡罗可靠度计算方法可定义完好概率为：
$$ {P_{\text{h}}} = \frac{M}{N} $$ (9) 式中：$ {P}_{{\mathrm{h}}} $——地基完好概率；
M——抽样次数中震陷量小于2 cm的次数；
N——蒙特卡洛分析法总的抽样次数。
2. 基于Kriging代理模型的震陷可靠度计算
2.1 Kriging代理模型的建立
Kriging模型是一种基于方差最小的无偏估计方法，它的原理是通过已知样本点的线性加权法来预测未知点的函数值，即已知加权系数插值就可求得变量空间内任一点的函数值。Kriging代理模型通常情况下由回归部分和随机误差两部分所组成。将其用输出变量S(x)与输入变量x表示为：
$$ S({\boldsymbol{x}}) = \sum\limits_{i = 1}^m {{\beta _i}} f({\boldsymbol{x}}) + {\textit{z}}({\boldsymbol{x}}) = f{({\boldsymbol{x}})^T}{\boldsymbol{\beta}} + {\textit{z}}({\boldsymbol{x}}) $$ (10) 式中：每个样本点中输入变量的个数为n，$ {\boldsymbol{x}} = [ {x_1},{x_2}, \cdots , {x_n} ]^T$，$ f(x) = {\left[ {{f_1}(x),{f_2}(x), \cdots ,{f_m}(x)} \right]^T} $为回归多项式基函数向量，m为回归多项式的数量；${\boldsymbol{\beta}} = {[{\beta _1},{\beta _2},\cdots,{\beta _m}]^T}$为多项式参数向量，z(x)为一均值为0，方差为$ {\sigma ^2} $的正态随机过程，该随机过程的协方差为：
$$ COV\left[{\textit{z}}(u),{\textit{z}}(v)\right]={\sigma }^{2}R({u,v}) $$ (11) 其中，R表示任意两点u，v的相关函数，通常取为高斯相关方程，即：
$$ R(u,v) = \exp \left\{ { - \theta {{(u - v)}^2}} \right\} $$ (12) 其中，$ \theta $为相关参数，可通过最大似然估计得到：
$$ \theta=\max \left\{ { - \left[ {\frac{1}{2}\ln \left( {\left| R \right|} \right)} \right] + \frac{k}{2}\ln \left( {{\sigma ^2}} \right)} \right\} $$ (13) 其中，R为相关矩阵，元素R=R(u,v)。
基于给定的样本点，多项式参数向量$\beta $与随机过程方差$ {\sigma ^2} $的估计值分别为：
$$ \left\{ {\begin{split} & {\hat {\boldsymbol{\beta}} = {{\left( {{{\boldsymbol{F}}^T}{{\boldsymbol{R}}^{ - 1}}{\boldsymbol{F}}} \right)}^{ - 1}}{{\boldsymbol{F}}^T}{{\boldsymbol{R}}^{ - 1}}{\boldsymbol{Y}}} \\ & {{{\hat {\boldsymbol{\sigma}} }^2} = \frac{1}{k}{{\left( {{\boldsymbol{Y}} - {\boldsymbol{F}}\hat {\boldsymbol{\beta}} } \right)}^T}{{\boldsymbol{R}}^{ - 1}}\left( {{\boldsymbol{Y}} -{\boldsymbol{ F}}\hat {\boldsymbol{\beta}} } \right)} \end{split}} \right. $$ (14) 其中，F为由回归多项式函数值构成的矩阵。
对于任意输入变量$ {x_0} $,假定$ {x_0} $与输入变量样本X之间的相关系数向量为$ {{\boldsymbol{r}}_0} = {\left[ {R\left( {{x_0},{x_1}} \right), \cdots ,R\left( {{x_0},{x_k}} \right)} \right]^T} $利用式（10）构建的Kriging模型表达式，可以得到与$ {x_0} $对应的系统响应值$ S({x_0}) $的预测值$ \hat S({x_0}) $服从正态分布$ N(\hat S({x_0}),{\hat \sigma _{\hat S}}^2({x_0})) $,$ S({x_0}) $的最佳线性无偏估计及均方误差可表示为：
$$ \left\{ {\begin{split} &{\hat S\left( {{x_0}} \right) = {f^T}({x_0})\hat {\boldsymbol{\beta}} + {{\boldsymbol{r}}_0}^T{{\boldsymbol{R}}^{ - 1}}({\boldsymbol{Y}} - {\boldsymbol{F}}\hat {\boldsymbol{\beta }})} \\ & {{{\hat \sigma }^2}_{\hat S}({x_0}) = {{\hat \sigma }^2}\left( {1 + {{\boldsymbol{u}}^T}{{({{\boldsymbol{F}}^T}{{\boldsymbol{R}}^{ - 1}}{\boldsymbol{F}})}^{ - 1}}{\boldsymbol{u}} - {{\boldsymbol{r}}_0}^T{{\boldsymbol{R}}^{ - 1}}{{\boldsymbol{r}}_0}} \right)} \end{split}} \right. $$ (15) 其中，$ {{{\boldsymbol{u}} = }}{{{{\boldsymbol{F}}}}^T}{{\boldsymbol{R}}^{ - 1}}{{\boldsymbol{r}}_0} - {\boldsymbol{f}} $。
本文进行震陷可靠度分析时，式（10）—（15）中应用Kriging模型构建和预测其过程，采用MATLAB中的DACE工具箱实现。
2.2 黄土地基数值模型
采用FLAC3D有限差分软件建立黄土地基数值模型，模型尺寸设置为15 m×15 m×15 m，模型网格数为
3375 ，本构模型选择Mohr-Coulomb弹塑性本构模型。在静力分析时，底面和侧面选用固定边界，限制底面与侧面的位移和速度，顶部为自由边界。动力分析与静力分析不同，由于地震荷载会存在波的反射，因此在模型底面设置静态边界，侧面设置为自由场边界，模拟土体在实际中的状态（图1）。本文选用三条地震波分别是Kobe地震波、Imperial地震波和一条人工合成波。为方便后续说明，这里将选用的三条地震波分别命名为地震波1、地震波2及地震波3。地震波1的持续时间为25 s，时间间隔为0.02 s，最大加速度为0.345g，地震波2的持续时间为40 s，时间间隔为0.01 s，最大加速度为0.313g，地震波3的持续时间为20 s，时间间隔为0.02 s，最大加速度为0.153g。图2为经过滤波以及基线校正后所选地震波的时程曲线。
为了研究不同地震水平作用下震陷变形规律，将其改变幅值的大小来满足不同工况的需要，得到 0.1g、0.2g、0.3g、0.4g、0.5g、0.6g、0.7g不同峰值加速度大小的7种水平。其计算所得震陷量结果如表1所示。
表 1 不同地震波及不同峰值加速度作用下地基震陷量Table 1. Seismic subsidence of foundation under different seismic waves and peak accelerations.峰值加速度/g 震陷量/cm 地震波1 地震波2 地震波3 0.1 0.72 1.95 2.65 0.2 2.37 8.40 13.44 0.3 9.10 16.02 21.62 0.4 17.83 21.44 29.52 0.5 19.78 25.29 37.06 0.6 20.08 30.67 40.98 0.7 20.48 35.84 46.98 2.3 震陷变形影响因素敏感性分析
岩土体材料参数存在着变异性，但土体泊松比的变异系数非常小，在考虑土性参数不确定时可将其看作常量。孙军杰等[17]通过理论分析，给出了非饱和黄土动残余应变与黏聚力、内摩擦角、初始孔隙比、土层重度、土层埋深以及地震动荷载之间的定量关系式。压缩模量是体现土体压缩性的指标之一，作为土体的力学性质，在分析地基土体变形或沉降时起着重要作用，而土体的黏聚力和内摩擦角反映土体的强度特征，在静力分析中，黄土地基静力参数中密度对于计算结果的影响较明显。因此，这里选择密度、弹性模量、黏聚力及内摩擦角四种参数。采用FLAC3D结合灰色关联分析对影响黄土地基震陷变形的因素做敏感性分析，求得其密度、弹性模量、黏聚力及摩擦角四个参数的灰色关联度为$ q = [ {0.656\;8},\;{0.856\;2},\;{0.668\;5},\;{0.728\;1} ] $，敏感性排序为：弹性模量>内摩擦角>黏聚力>密度。
2.4 土性参数分布概率模型
本节选取密度（ρ）、压缩模量（Es）、黏聚力（c）及内摩擦角（φ）四种参数作为黄土震陷性评价的参数指标来进行分布概率模型研究。为了全面分析不同地貌单元4种土性参数的最优概率分布，选用可以包含大部分不确定性因素的概率分布形式包括正态分布、对数正态分布和威布尔分布进行假设检验。从而确定每个参数的最优概率分布形式[18]。
为获取原状黄土地基土性不同参数的分布概率模型，基于引汉济渭工程的渭河二级阶地地貌土体为例，通过对原状黄土的各种物理力学指标进行统计分析，得出各指标服从的概率密度函数及分布参数，图3所示为渭河二级阶地分布概率模型图，其中$ f\left( x \right) $表示概率密度函数。
![]()
图 3 不同参数的概率密度分布图Figure 3. Probability density distribution plots of different parameters由图3可知，从分布形态上来看，$ \rho $值的正态分布和对数正态分布整体较一致，两者均属于左偏态；其余三种土性参数正态分布、对数正态分布及威布尔分布三者分布较离散，差异性较大。
通过K-S检验法对4种土性参数的3种分布概率模型进行检验，求出样本值的理论累计概率分布与经验累计概率分布的最大差值（Dmax），与由显著性水平和样本数确定临界值（$ D_n^\alpha $）进行比较，计算结果如表2所示。四种参数均可接受正态分布、对数正态分布和威布尔分布。$ c $、$ {E_{\mathrm{s}}} $值的最优分布是正态分布，$ \varphi $、$ \rho $值的最优分布是威布尔分布，考虑到正态分布的优良性质，将正态分布作为4种土性参数的分布概率模型用于震陷可靠度计算。
表 2 分布假设检验结果Table 2. Distribution hypothesis test results检验参数 样本量 验证结果$ {D_{\max }} $ 可接受的临界值
$ D_n^\alpha /\left( {\alpha = 0.05} \right) $正态分布 对数正态分布 威布尔分布 结果 $ {D_{\max }} $ 结果 $ {D_{\max }} $ 结果 $ {D_{\max }} $ 内摩擦角 24 √ 0.180 √ 0.223 √ 0.093 0.273 黏聚力 24 √ 0.099 √ 0.125 √ 0.102 0.273 压缩模量 24 √ 0.094 √ 0.146 √ 0.164 0.273 密度 48 √ 0.150 √ 0.185 √ 0.115 0.196 2.5 基于Kriging代理模型的震陷可靠度计算方法
本节基于Kriging代理模型对地基震陷可靠度进行计算，这里进行
10000 次模拟，计算步骤如下：（1）根据前文统计出的土性参数（密度、压缩模量、黏聚力、摩擦角）的概率分布模型，确定地基土体参数的均值、标准差、分布类型等统计特性。
（2）FLAC3D6.0内置有Python编程语言，可以实现蒙特卡洛抽样与连续计算，利用Itasca开发的专门用于Python扩展编程的程序库，通过编程实现随机变量拉丁超立方抽样（LHS）、模型的建立以及计算，即会产生N组计算方案$ \left(\rho_1,E_{\mathrm{s}1},c_1,\varphi_1\right),\left(\rho_2,E_{\mathrm{s}2},c_2,\varphi_2\right),\cdots,(\rho_n,E_{\mathrm{s}n},c_n, \varphi_n) $，然后计算出对应的响应值。将计算模型文件保存为“n.f3sav”，后续模型按顺序编号，并将其作为源文件以便后续提取。
（3）对地震波设计不同的工况组合，计算每组工况下LHS的样本所对应的震陷量，并保存计算模型。
（4）利用Python编程语言从结果文件中批量提取竖向变形。
（5）采用MATLAB软件分别建立不同工况下的Kriging代理模型，以4种土体参数为输入，相应的地基震陷量为输出，对代理模型进行训练，得到满足精度要求的代理模型。经适当训练的代理模型能够较好地逼近实际情况，在此基础上可以十分方便地预测震陷值从而实现震陷可靠度的计算（图4）。
![]()
图 4 基于Kriging代理模型的震陷可靠度计算流程Figure 4. Calculation process of seismic subsidence reliability based on the Kriging surrogate model3. 算例分析
为验证本文提出方法的适用性，本节以引汉济渭工程为背景结合Kriging代理模型的震陷概率计算方法开展黄土地基震陷可靠度分析。
（1）最大可靠度
表3为不同地震波及不同地震峰值加速度作用下地基震陷的破坏概率，以渭河二级阶地为例。
表 3 不同地震波作用下地基震陷破坏概率Table 3. Probability of foundation subsidence failure under different seismic wave effects加速度/g 地震波1 地震波2 地震波3 0.1 0 0 0 0.2 0 0 0 0.3 0 0 0 0.4 0 0.072 0.116 0.5 0 0.17 0.378 0.6 0 0.232 0.704 0.7 0.002 0.264 0.888 由表3可知，在地震波1的作用下，该地基土体在地震波峰值加速度为0.7g时会出现破坏的概率，在地震波2和地震波3的作用下，在峰值加速度达到0.4g时会出现破坏的概率。三条地震波在峰值加速度达到最大时，其产生的破坏概率也有巨大差异，地震波1在峰值加速度为0.7g时破坏概率为0.002，地震波2在峰值加速度为0.7g时破坏概率为0.264，地震波3在峰值加速度为0.7g时破坏概率为0.888。
依据式（4）求得最大可靠度指标，图5为不同地震波作用下地基震陷的可靠度指标随峰值加速度的变化规律，最大可靠度指标的范围为−1.216～4.526。总体上可靠度指标随峰值加速度的增加呈非线性减小。但三条地震波的减小斜率并不相同，在地震波3作用下，可靠度指标随峰值加速度的变化斜率最大，说明在地震波3作用下，地基的可靠度受地震波峰值加速度的影响最大。对于已知地震波峰值加速度，可以快速粗略估计地基震陷的破坏概率，而不是单纯以震陷量来评价，这在风险评估中具有更为重要的意义。
![]()
图 5 可靠度分析获得的地基震陷最大可靠度Figure 5. Maximum reliability index of foundation seismic subsidence obtained from reliability analysis（2）最小可靠度
表4为不同地震波及不同地震峰值加速度作用下地基震陷的破坏概率，以渭河二级阶地为例。由表4可知，在地震波1的作用下，该地基土体在地震波峰值加速度为0.1g～0.7g时均会出现完好概率，在地震波2和地震波3的作用下，在峰值加速度分别达到0.4g及以后和0.3g及以后完好概率均为0。
表 4 不同地震波作用下地基震陷完好概率Table 4. Probability of intact seismic subsidence of foundation under different seismic wave effects加速度/g 地震波1 地震波2 地震波3 0.1 0.946 0.854 0.842 0.2 0.392 0.094 0.832 0.3 0.238 0.004 0 0.4 0.01 0 0 0.5 0.018 0 0 0.6 0.012 0 0 0.7 0.002 0 0 依据式（8）求得最小可靠度指标，图6为在不同地震波作用下地基震陷的最小可靠度随峰值加速度的变化规律，最小可靠度指标的变化范围为−2.878～1.607。从整体来说，随着地震峰值加速度的增大，地基在地震作用下的最小可靠度指标逐渐降低。当地震峰值加速度为0.1g时，震陷最小可靠度较高，都为正值；当地震峰值加速度为0.2g时，地震最小可靠度显著减小，且超过0.2g以后最小可靠度均为负值。
![]()
图 6 可靠度分析获得的地基震陷的最小可靠度指标Figure 6. Minimum reliability index of foundation seismic subsidence obtained from reliability analysis（3）变异系数对震陷可靠度的影响
为了更好地分析随机变量的变异性大小对震陷可靠度的影响，本文计算了各变量在不同变异系数组合情况下，四种土体参数变异系数随地基震陷可靠度的变化情况，工况组合见表5。
表 5 各参数变异系数工况组合表Table 5. Combination table of variation coefficient for each parameter工况 COV 密度 弹性模量 黏聚力 摩擦角 1-1 0.01 0.3 0.2 0.3 1-2 0.05 1-3 0.1 1-4 0.15 1-5 0.2 2-1 0.05 0.05 0.2 0.3 2-2 0.1 2-3 0.2 2-4 0.3 2-5 0.4 3-1 0.05 0.3 0.05 0.3 3-2 0.1 3-3 0.2 3-4 0.3 3-5 0.4 4-1 0.05 0.3 0.2 0.1 4-2 0.2 4-3 0.3 4-4 0.4 4-5 0.5 计算结果如图7所示。由图可知，随各参数变异系数的增加，震陷最大可靠度逐渐减小，而最小可靠度逐渐增大。当$ COV(\rho) $从0.01增加至0.2，相应的$ {\beta _{\text{d}}} $从3.72减小至3.05，最小可靠度（$ {\beta _{\text{h}}} $）从−1.72增加至−1.55，降幅为21.97%，增幅为10.96%；当$ COV(E_{\mathrm{s}}) $从0.05增加至0.4，相应的$ {\beta _{\text{d}}} $从3.89降至3.29，$ {\beta _{\text{h}}} $从−1.89增加至−1.64，降幅为18.24%，增幅为15.24%；当$ COV(c) $从0.05增加至0.4，$ {\beta _{\text{d}}} $从4.26降至2.89，$ {\beta _{\text{h}}} $从−1.81增加至−1.60，降幅为47.40%，增幅为13.13%；当$ COV(\varphi)$从0.1增加至0.5，$ {\beta _{\text{d}}} $从3.72降至2.74，$ {\beta _{\text{h}}} $从−1.99增加至−1.63，降幅为35.77%，增幅为22.09%。对比数据，在同样的增幅下，最大可靠度的变化幅度比最小可靠度的变化幅度大说明最大可靠度对变异系数更为敏感。计算各个参数最大可靠度起末两点斜率的绝对值，分别为3.526、1.714、3.914和2.45，可看出黏聚力变异系数对震陷最大可靠度影响更为显著。
![]()
图 7 不同参数变异系数对震陷可靠度的影响规律Figure 7. The influence of different parameter coefficient of variations on seismic subsidence reliability4. 结论
（1）Kriging代理模型可以在小样本抽样的情况下得到较好的近似拟合效果，达到精度要求，提高了震陷可靠度的计算效率。
（2）采用震陷可靠度方法来评价地基土体的震陷性，能够合理地考虑土性参数的变异性，更加符合实际情况，具有更好的可靠性和适用性，对于已知地震波峰值加速度，可以快速粗略估计地基震陷的破坏概率，而不是单纯的以震陷量来评价，这在风险评估中具有更为重要的意义。
（3）综合4种土体参数的变异系数对震陷可靠度的影响可以发现，最大可靠度对各个参数的变异系数更为敏感，此外四种土体参数中黏聚力的变异系数对震陷最大可靠度的影响更为显著。
-
![]()
图 1 研究区地理位置及相关信息
Figure 1. Location of the Ren’eyong valley and related information of the study area
![]()
图 10 非火烧区与火烧区坡积物对比
Figure 10. Comparison of slope sediments in non-fire area and fire areas
![]()
图 11 火后泥石流的携带坡面烧毁的植被
Figure 11. Site photo of the burned vegetation carried by post-fire debris flow
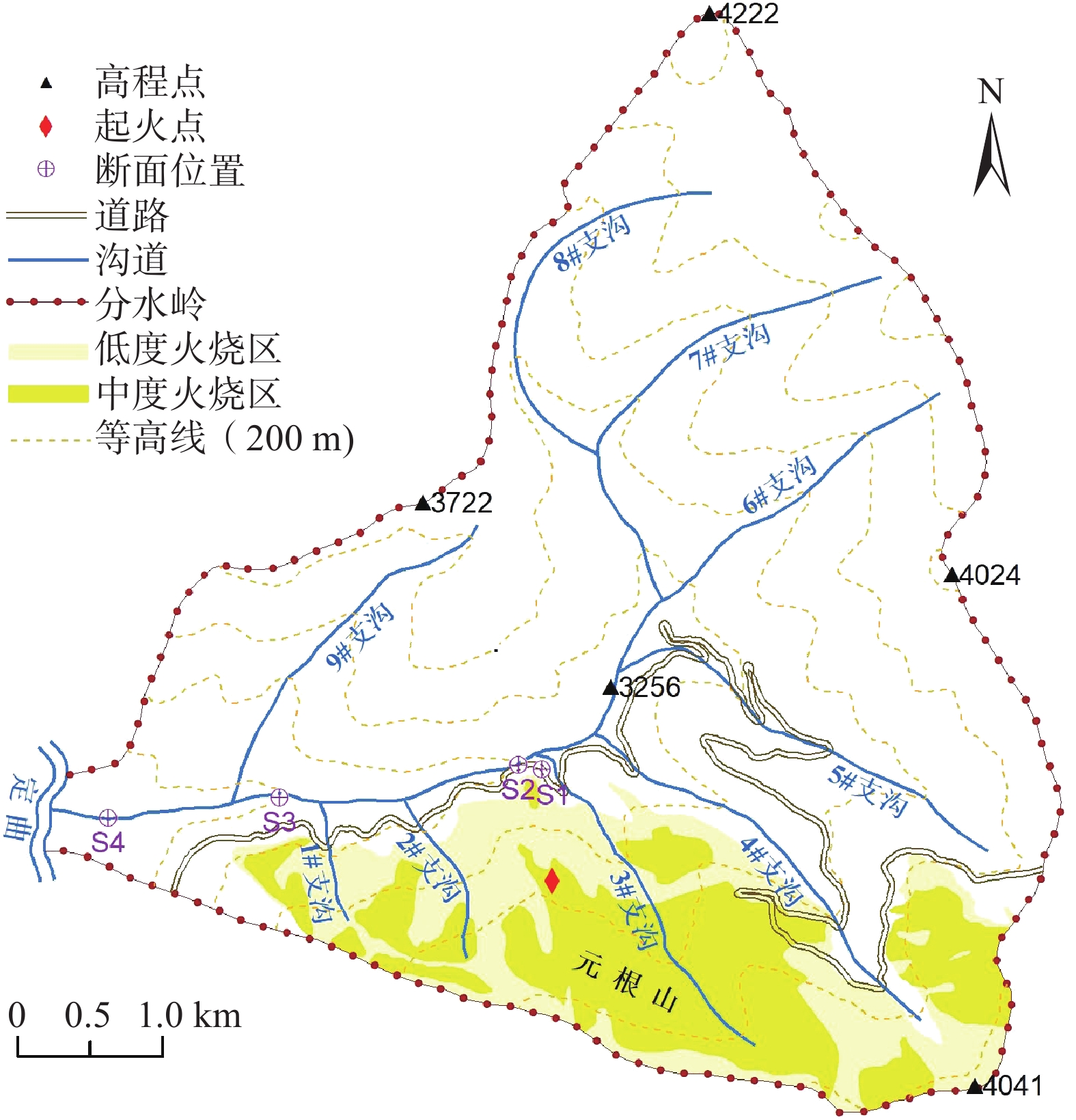
表 1 1#—3#支沟基本信息
Table 1 Geographic information of branches No.1−No.3
编号 流域面积/km2 沟长/m 平均坡度/（°） 1# 0.37 544 27 2# 0.73 755 26 3# 2.30 836 15 
下载: 导出CSV
表 2 1#—3#支沟火烧强烈程度及面积统计
Table 2 Summary of fire severity classification and affected areas of branches No.1−No.3
编号 火烧面积/km2 轻度火烧/km2 中度火烧/km2 1#支沟 0.31 0.21 0.10 2#支沟 0.64 0.45 0.19 3#支沟 2.11 0.6 1.51
下载: 导出CSV
表 3 泥石流基本情况
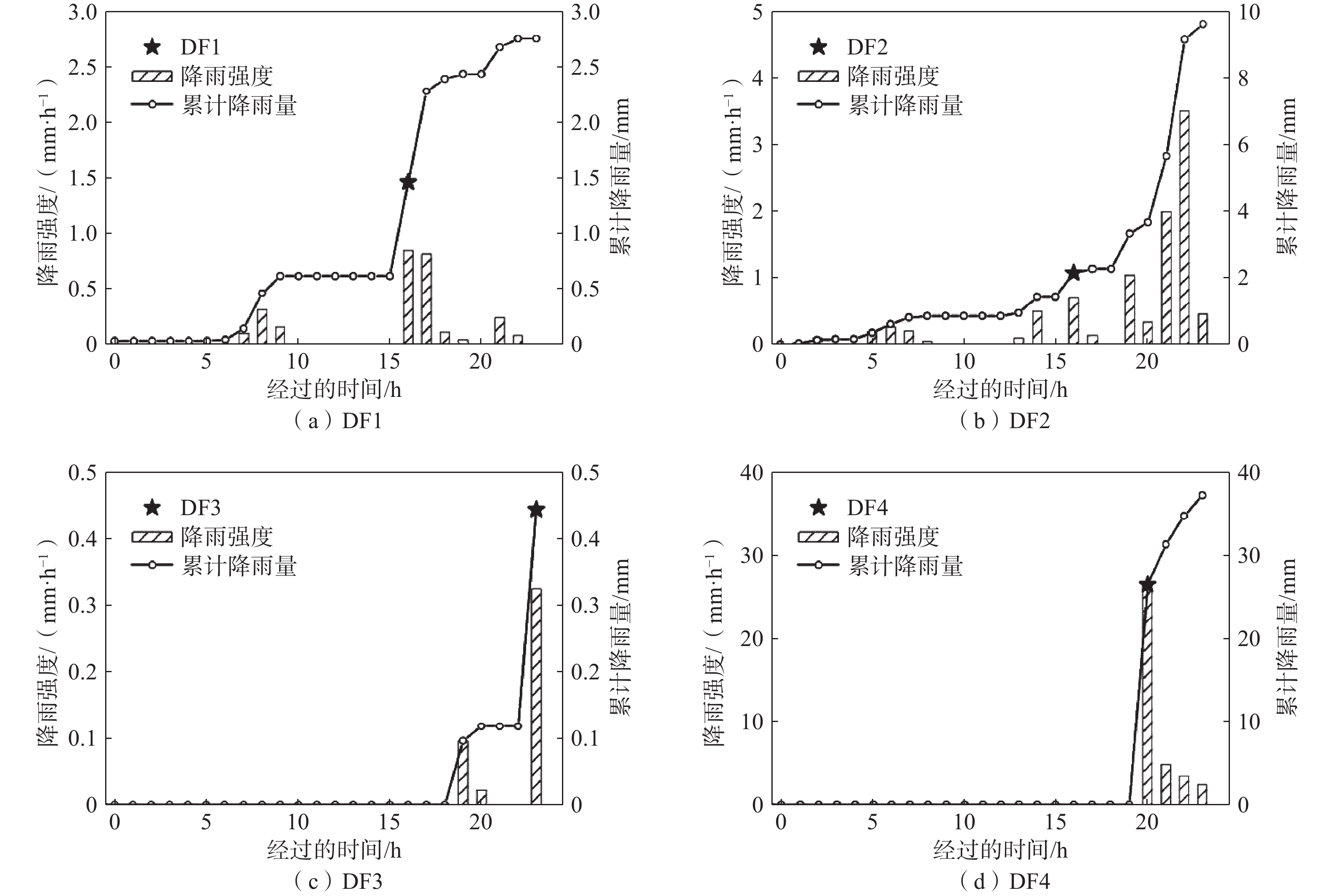
Table 3 Basic property information of the debris flows
序号 时刻 位置 冲出量
/（104 m3）前期3 d
降雨量/mmDF1 2014年6月8日16:08 3# 0.8 1.11 DF2 2014年6月30日16:00 3# 1.4 14.84 DF3 2014年7月10日23:20 3# 0.5 0.81 DF4 2015年8月24日19:43 1#、2#、3# 2.2 39.97
下载: 导出CSV
表 4 3处雨量站基本情况
Table 4 Summary of the basic property information of the three rain gauges
序号 气象站名 海拔/m 距泥石流沟
距离/km精度/mm $权重参数$ 1 正斗站 2858 4.10 0.1 0.577 2 热打站 3363 5.56 0.1 0.313 3 阿都站 2783 9.40 0.1 0.110
下载: 导出CSV
-
[1] LARSEN I J,MACDONALD L H,BROWN E,et al. Causes of post-fire runoff and erosion:Water repellency,cover,or soil sealing?[J]. Soil Science Society of America Journal,2009,73(4):1393 − 1407. DOI: 10.2136/sssaj2007.0432
[2] SCOTT,W WOODS,VICTORIA N,et al. The effects of soil texture and ash thickness on the post-fire hydrological response from ash-covered soils[J]. Journal of Hydrology,2010,393(3-4):274 − 286. DOI: 10.1016/j.jhydrol.2010.08.025
[3] MACDONALD L H,HUFFMAN E L. Post-fire soil water repellency[J]. Soil Science Society of America Journal,2004,68(5):1729 − 1734. DOI: 10.2136/sssaj2004.1729
[4] NYMAN P,SHERIDAN G,LANE P N J. Synergistic effects of water repellency and macropore flow on the hydraulic conductivity of a burned forest soil,south-east Australia[J]. Hydrological Processes,2010,24(20):2871 − 2887. DOI: 10.1002/hyp.7701
[5] MOODY J A,EBEL B A,NYMAN P,et al. Relations between soil hydraulic properties and burn severity[J]. International Journal of Wildland Fire,2016,25(3):279. DOI: 10.1071/WF14062
[6] MOODY J A,EBEL B A. Hyper-dry conditions provide new insights into the cause of extreme floods after wildfire[J]. CATENA,2012,93(93):58 − 63.
[7] KEAN J W,STALEY D M,CANNON S H. In situ measurements of post-fire debris flows in southern California:comparisons of the timing and magnitude of 24 debris-flow events with rainfall and soil moisture conditions[J]. Journal of Geophysical Research,2011,116(F4):F04019.
[8] SMITH H G,SHERIDAN G J,LANE P N J,et al. Paired Eucalyptus forest catchment study of prescribed fire effects on suspended sediment and nutrient exports in south-eastern Australia[J]. International Journal of Wildland Fire,2010,19(5):624. DOI: 10.1071/WF08208
[9] JORDAN P. Post-wildfire debris flows in southern British Columbia,Canada[J]. International Journal of Wildland Fire,2016,25(3):322. DOI: 10.1071/WF14070
[10] CONEDERA M,PETER L,MARXER P,et al. Consequences of forest fires on the hydrogeological response of mountain catchments:a case study of the Riale Buffaga,Ticino,Switzerland[J]. Earth Surface Processes and Landforms,2003,28(2):117 − 129. DOI: 10.1002/esp.425
[11] 胡卸文,王严,杨瀛. 火后泥石流成灾特点及研究现状[J]. 工程地质学报,2018,26(6):1562 − 1573. [HU Xiewen,WANG Yan,YANG Ying. Research actuality and evolution mechanism of post-fire debris flow[J]. Journal of Engineering Geology,2018,26(6):1562 − 1573. (in Chinese with English abstract) DOI: 10.13544/j.cnki.jeg.2018-073 HU Xiewen, WANG Yan, YANG Ying. Research actuality and evolution mechanism of post-fire debris flow[J]. Journal of Engineering Geology, 2018, 26（6）1562-1573（in Chinese with English abstract） DOI: 10.13544/j.cnki.jeg.2018-073
[12] 王严,胡卸文,杨瀛,等. 火烧迹地土壤斥水性和渗透性变化特性[J]. 水文地质工程地质,2019,46(6):40 − 45. [WANG Yan,HU Xiewen,YANG Ying,et al. Research on the change in soil water repellency and permeability in burned areas[J]. Hydrogeology & Engineering Geology,2019,46(6):40 − 45. (in Chinese with English abstract) DOI: 10.16030/j.cnki.issn.1000-3665.2019.06.06 WANG Yan, HU Xiewen, YANG Ying, et al. Research on the change in soil water repellency and permeability in burned areas[J]. Hydrogeology & Engineering Geology, 2019, 46（6）40-45（in Chinese with English abstract） DOI: 10.16030/j.cnki.issn.1000-3665.2019.06.06
[13] 任云,胡卸文,王严,等. 四川省九龙县色脚沟火后泥石流成灾机理[J]. 水文地质工程地质,2018,45(6):150 − 156. [REN Yun,HU Xiewen,WANG Yan,et al. Disaster mechanism of the Sejiao post-fire debris flow in Jiulong County of Sichuan[J]. Hydrogeology & Engineering Geology,2018,45(6):150 − 156. (in Chinese with English abstract) DOI: 10.16030/j.cnki.issn.1000-3665.2018.06.22 REN Yun, HU Xiewen, WANG Yan, et al. Disaster mechanism of the Sejiao post-fire debris flow in Jiulong County of Sichuan[J]. Hydrogeology and Engineering Geology, 2018, 45（6）150-156（in Chinese with English abstract） DOI: 10.16030/j.cnki.issn.1000-3665.2018.06.22
[14] 黄健,胡卸文,金涛,等. 四川西昌 “3•30” 火烧区响水沟火后泥石流成灾机理[J]. 中国地质灾害与防治学报,2022,33(3):15 − 22. [HUANG Jian,HU Xiewen,JIN Tao,et al. Mechanism of the post-fire debris flow of the Xiangshui gully in “3•30” fire area of Xichang,Sichuan Province[J]. The Chinese Journal of Geological Hazard and Control,2022,33(3):15 − 22. (in Chinese with English abstract) HUANG Jian, HU Xiewen, JIN Tao, et al. Mechanism of the post-fire debris flow of the Xiangshui gully in “3·30” fire area of Xichang, Sichuan Province[J]. The Chinese Journal of Geological Hazard and Control, 2022, 33（3）15-22（in Chinese with English abstract）
[15] 杨相斌,胡卸文,曹希超,等. 四川西昌电池厂沟火后泥石流成灾特征及防治措施分析[J]. 中国地质灾害与防治学报,2022,33(4):1 − 8. [YANG Xiangbin,HU Xiewen,CAO Xichao,et al. Analysis on disaster characteristics and prevention measures of the post-fire debris flow in Dianchichang gully,Xichang of Sichuan Province[J]. The Chinese Journal of Geological Hazard and Control,2022,33(4):1 − 8. (in Chinese with English abstract) DOI: 10.16031/j.cnki.issn.1003-8035.202203039 YANG Xiangbin, HU Xiewen, CAO Xichao, et al. Analysis on disaster characteristics and prevention measures of the post-fire debris flow in Dianchichang gully, Xichang of Sichuan Province[J]. The Chinese Journal of Geological Hazard and Control, 2022, 33（4）1-8（in Chinese with English abstract） DOI: 10.16031/j.cnki.issn.1003-8035.202203039
[16] CHEN J C,HUANG W S,JAN C D,et al. Recent changes in the number of rainfall events related to debris-flow occurrence in the Chenyulan Stream Watershed,Taiwan[J]. Natural Hazards and Earth System Science,2012,12(5):1539 − 1549. DOI: 10.5194/nhess-12-1539-2012
[17] 刘世康,范宣梅,王文松,等. 降雨模式对震后泥石流起动模式影响的试验研究—以九寨天堂沟为例[J]. 地质科技通报,2022,41(6):278 − 286. [LIU Shikang,FAN Xuanmei,WANG Wensong,et al. Experimental study on the effect of rainfall patterns on the failure mode of debris flows after earthquakes:A case study of Tiantanggou, Jiuzhai[J]. Bulletin of Geological Science and Technology,2022,41(6):278 − 286. (in Chinese with English abstract) [LIU Shikang, FAN Xuanmei, WANG Wensong, et al. Experimental study on the effect of rainfall patterns on the failure mode of debris flows after earthquakes: A case study of Tiantanggou, Jiuzhai[J]. Bulletin of Geological Science and Technology, 2022, 41(6): 278-286. (in Chinese with English abstract)
计量
- 文章访问数: 683
- HTML全文浏览量: 2019
- PDF下载量: 263
邮件订阅
RSS