Experiment on the effect of forward and reverse rotation speeds of rockfall on normal restitution coefficient
-
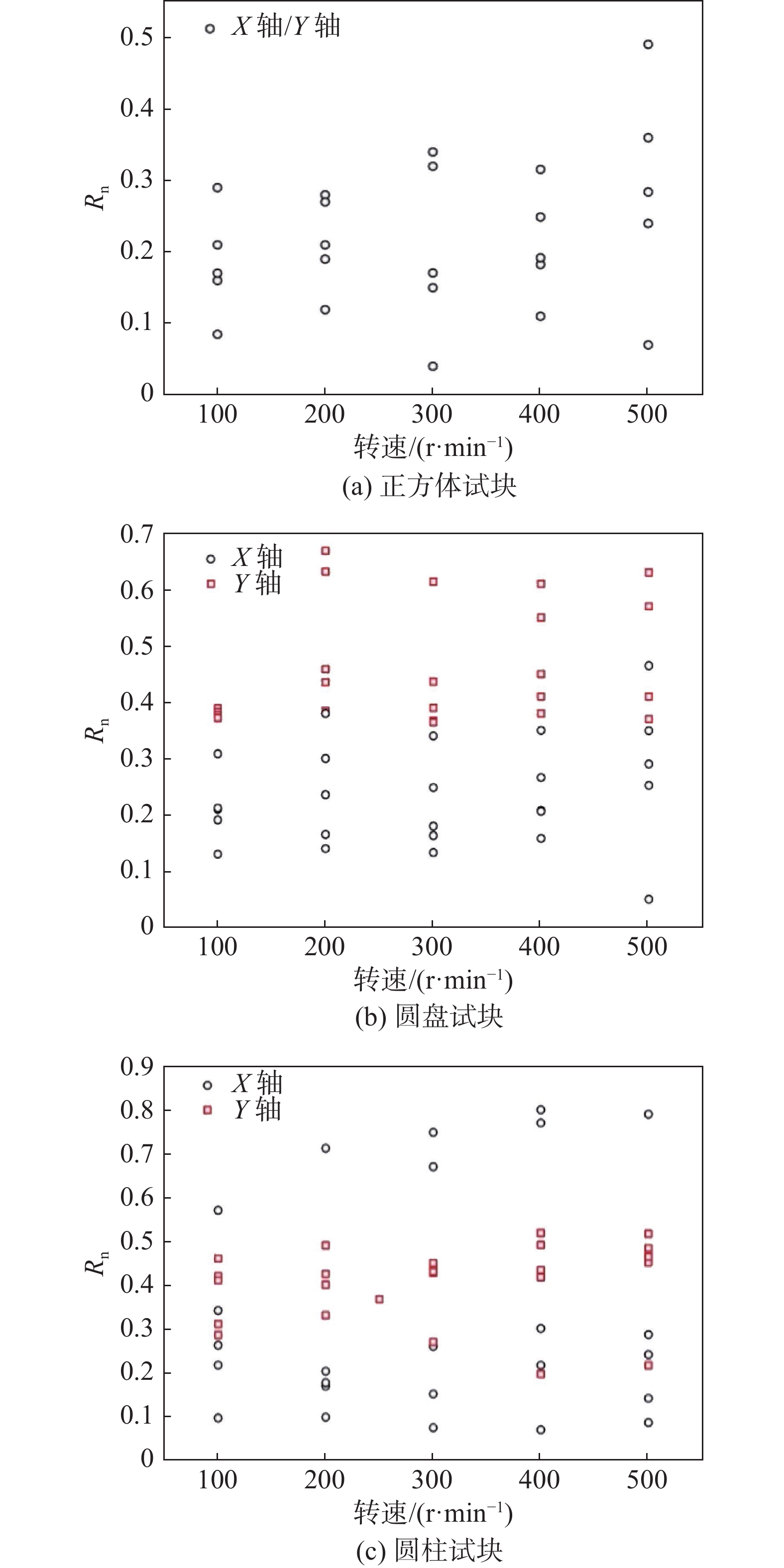
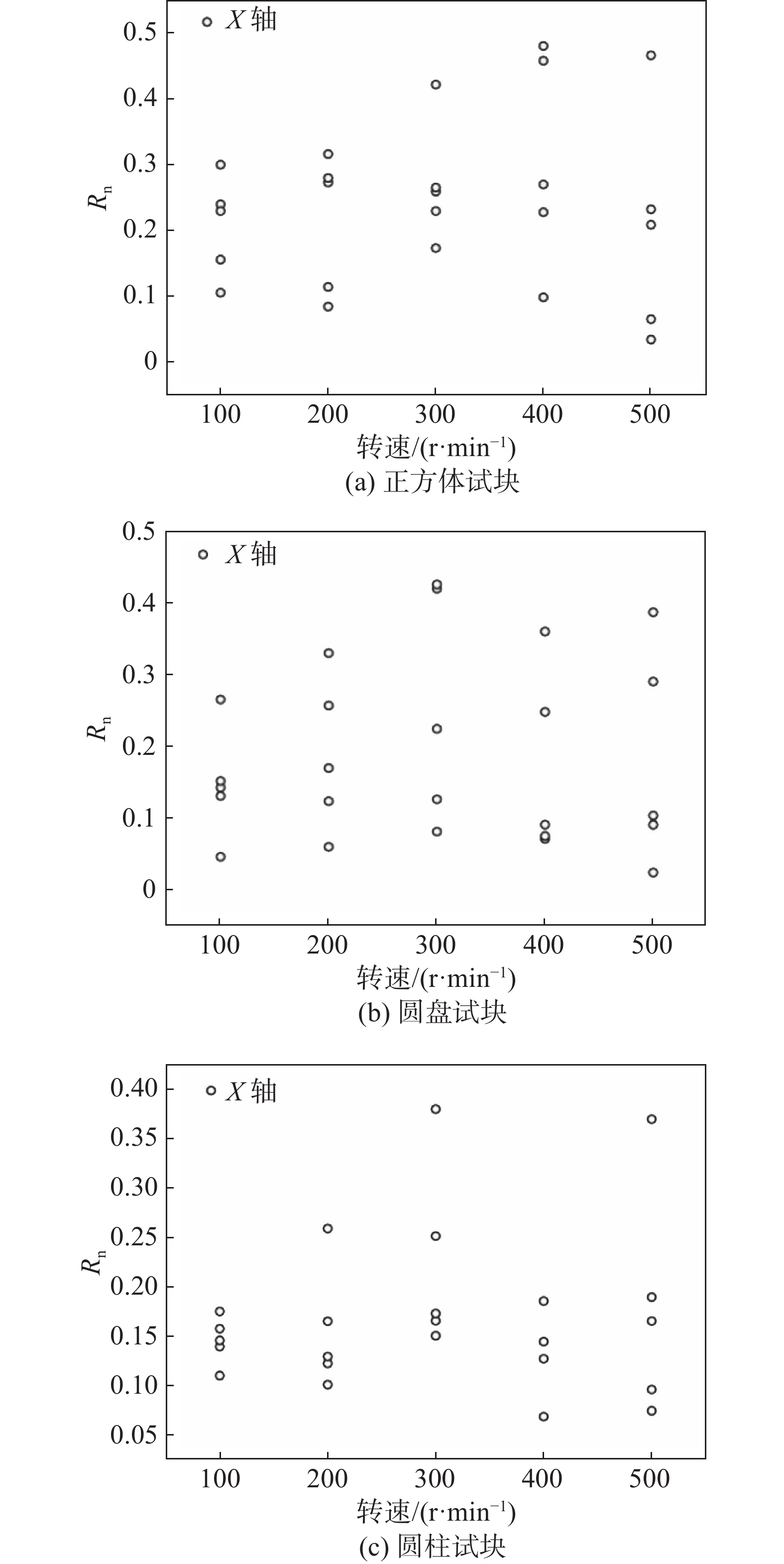
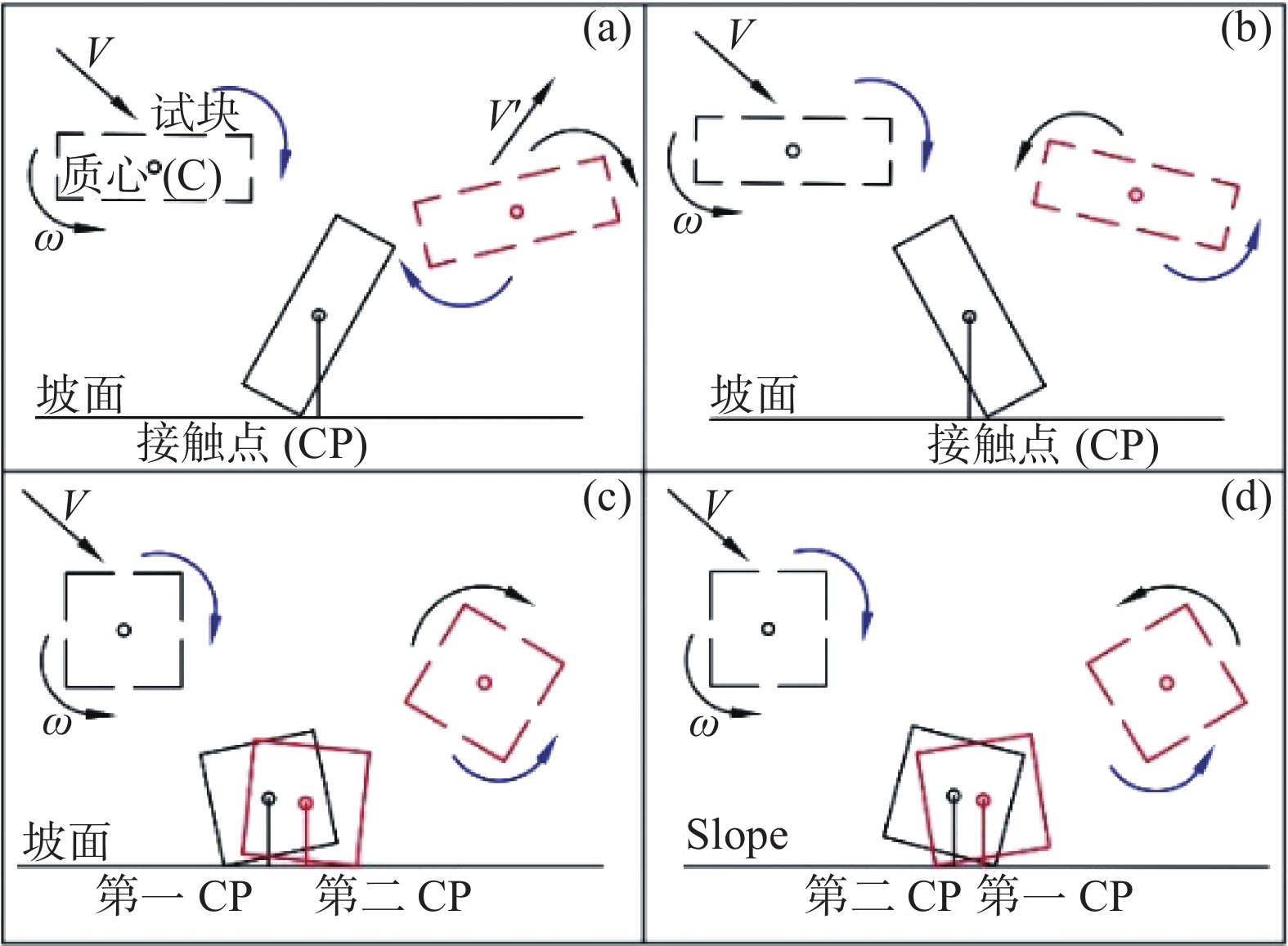
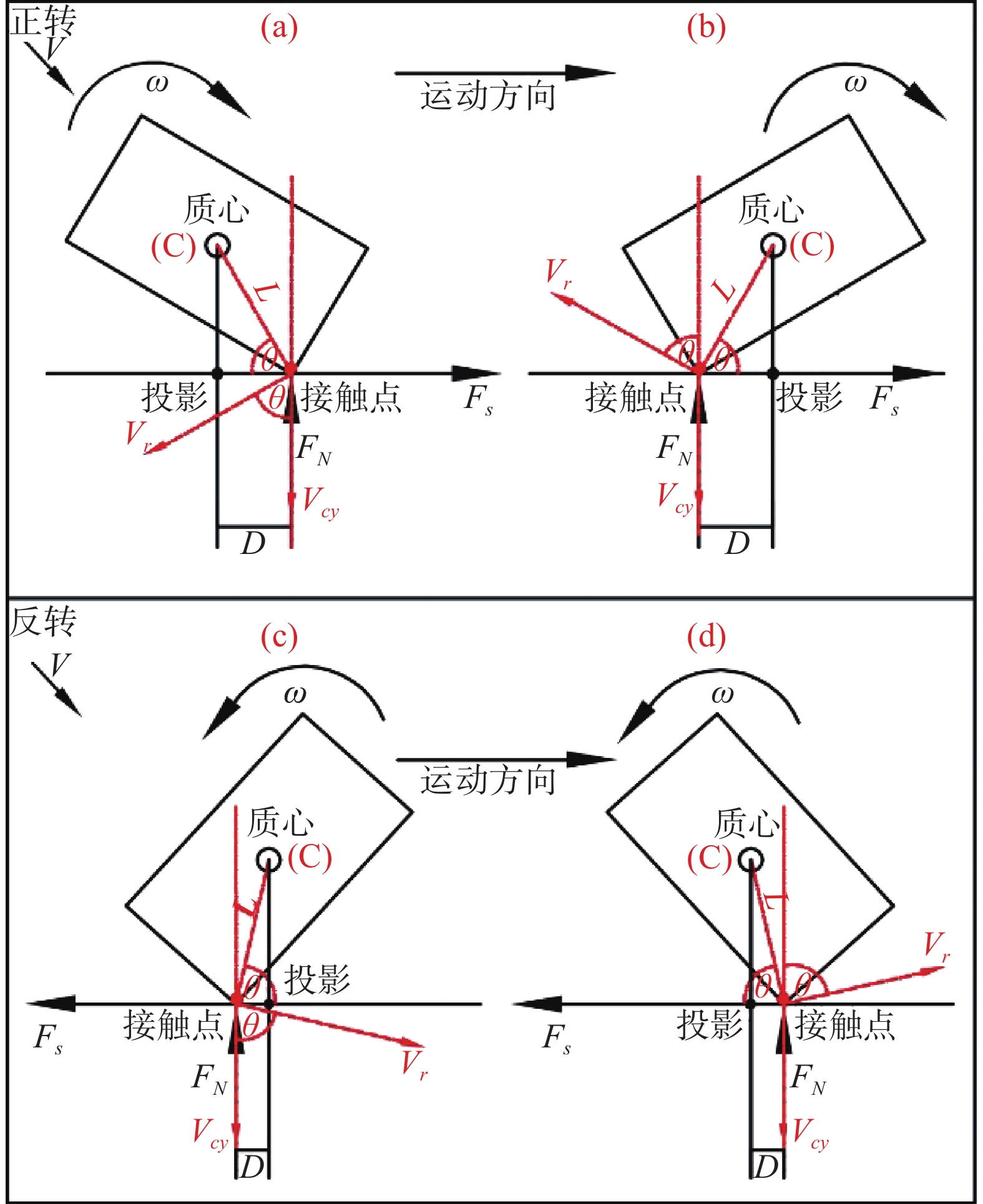
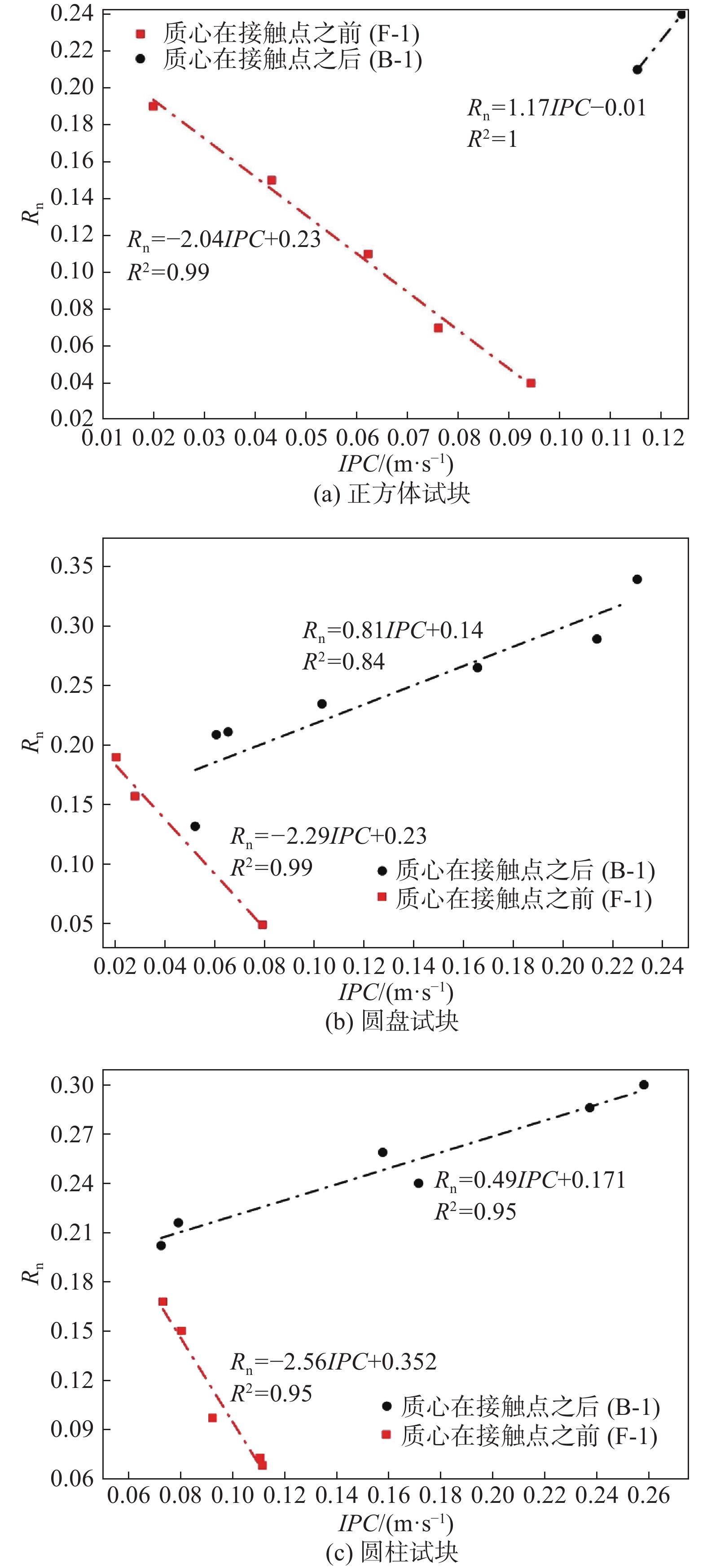
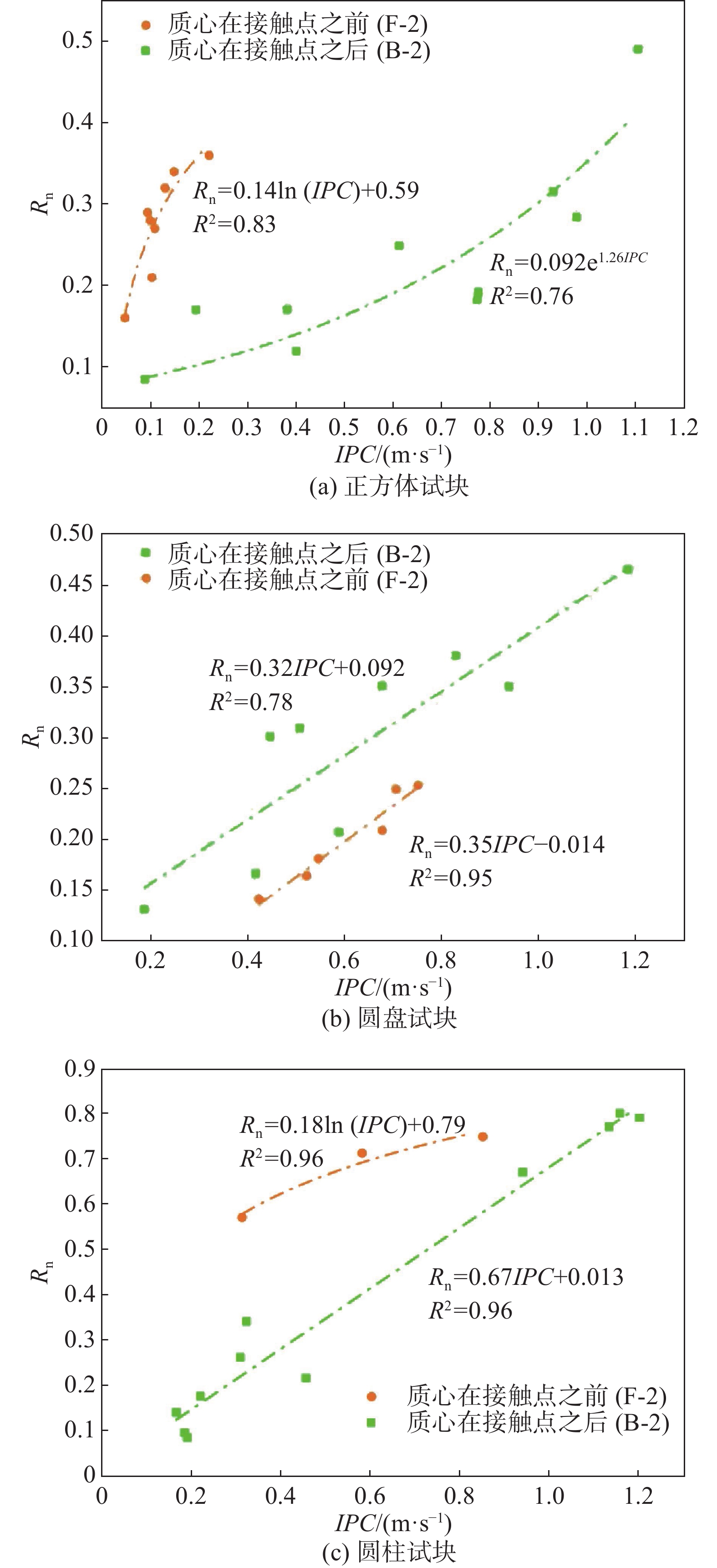
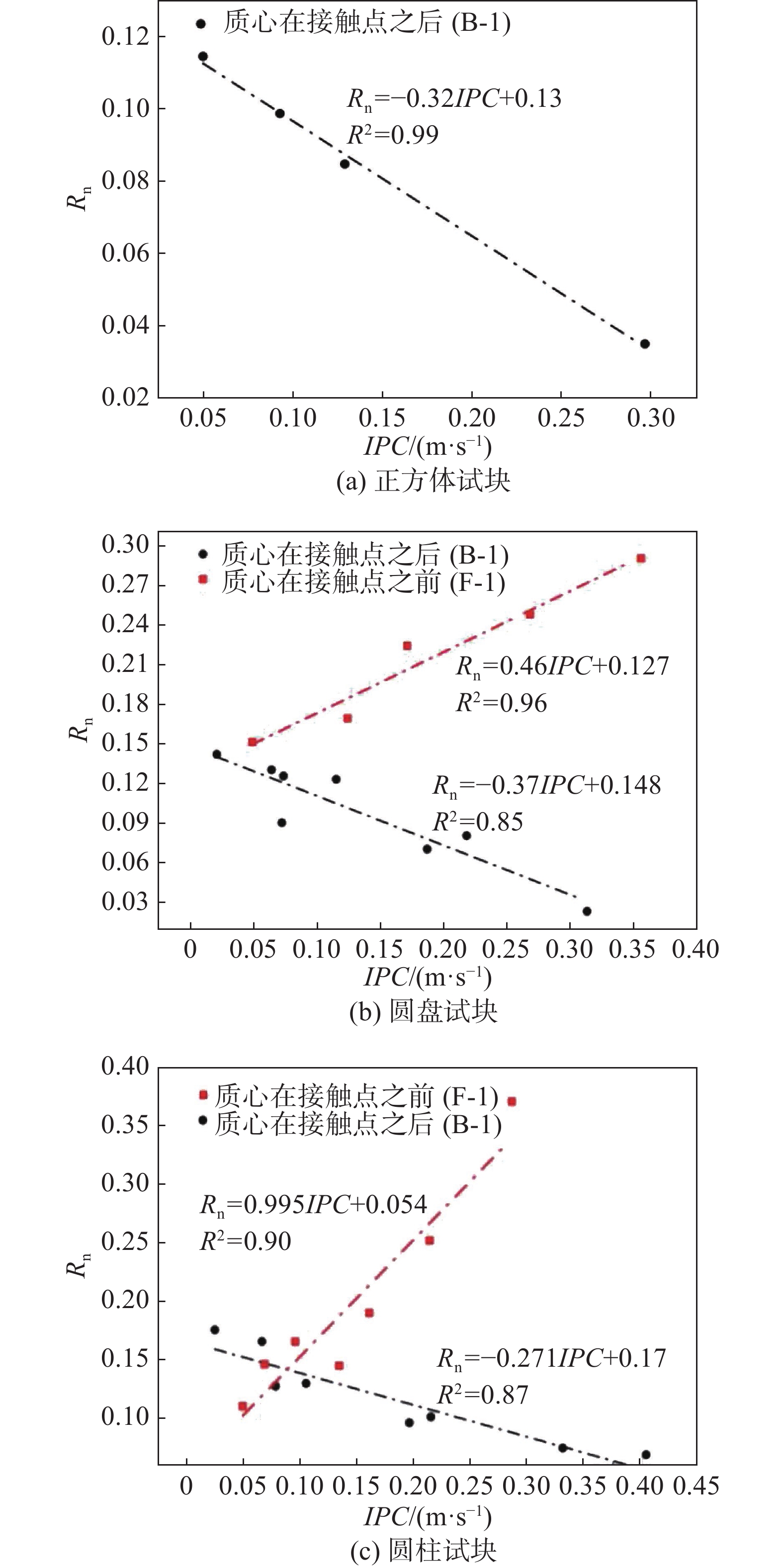
摘要: 为探究落石正转和反转转速对法向恢复系数（Rn）的影响，选制正方、圆盘和圆柱三种典型形状试块，通过专门研发的落石碰撞测试装置，开展不同正转和反转转速下试块绕X和Y轴与坡面的碰撞测试。试验结果表明：圆盘和圆柱状试块绕Y轴旋转时（近似正碰），转速对Rn基本无影响；3种形状试块绕X轴旋转时（非正碰），转速和Rn存在一定相关性，但Rn还受到试块形状和冲击姿态联合影响。为此，引入综合变量-冲击姿态系数（IPC）来量化转速对Rn的影响。鉴于不同冲击姿态下法向冲击力对Rn的力学作用机制存在差异，对试块冲击回弹特征采取分类探讨。一次冲击回弹型，正转试验中质心（C）在接触点（CP）之后和C在CP之前条件下，IPC与Rn分别呈线性正相关和负相关关系；反转试验结果则正好相反。二次冲击回弹型，无论正转或反转，第一次冲击C在CP之前或之后，各形状试块IPC与Rn均为强正相关，但各工况下的相关规律并不一致。这些获得的结论基本揭示了转速对Rn的影响关系，同时为转动异形落石冲击回弹过程的精准预测提供了参考。Abstract: In order to explore the effect of forward and reverse rotation speeds of rockfall on normal restitution coefficient (Rn), three typical blocks of cube, disc and cylinder were customized, and the impact tests of each block with slope at different forward and reverse rotation speeds in X and Y axes were carried out through the specially developed rockfall impact test device. Results show that the rotation speed has no effect on Rn when the disc and the cylinder shaped blocks rotate around the Y-axis (approximately normal impact); when the three shaped blocks rotate along the X-axis (non-normal impact), there exists a certain correlation between the rotation speed and Rn, but Rn is also affected by the block shape and impact posture. Thus, a comprehensive variable - impact posture coefficient (IPC) was introduced to quantify the effect of rotation speed on Rn. In view of the difference of the mechanical action mechanism of normal impact force on Rn under different impact posture, the impact-rebound characteristics of the blocks were classified and discussed. For the type of rebounding after only one impact, IPC and Rn have linear positive correlation and negative correlation respectively when the mass center (C) is behind and in front of the contact point (CP) in the forward rotation test, and the results of the reverse rotation test were just the opposite. For the type of rebounding after two impacts, regardless of forward or reverse, whether C is behind or in front of CP during the first impact, Rn and IPC of each shaped block are strongly positive correlation, yet the relevant laws are not consistent under various working conditions. These conclusions basically reveal the influence of rotation speed on Rn, and provide a reference for accurate prediction of impact-rebound process of rotating irregular rockfall.
-
0. 引言
滑坡是一种频繁且严重的地质灾害，极大地威胁着人民的生命财产安全[1-2]。天然碎石土边坡分布广泛，尤其是在南方山地丘陵地区，在发生的各类滑坡中，碎石土滑坡占比接近80%[3-6]。许多学者对砂质和岩质边坡的稳定性开展研究，并取得不少成果，然而针对碎石土边坡的成果十分有限。因此，有必要对碎石土边坡的失效机理进行研究，为评估其稳定性提供合理的参考。
众多研究人员对碎石土边坡开展了大量的研究并取得了显著的研究成果，主要集中在理论分析、数值分析、试验研究三个方面。极限平衡法是边坡稳定性分析最早也最常用的一种理论分析方法，其理论基础是莫尔-库伦强度准则和静力平衡原理分析边坡破坏模式下的受力状态，根据边坡潜在破坏面的滑移体上沿剪切方向的抗剪力和剪切力之间的关系来计算边坡的安全系数[7-9]。然而，极限平衡法在计算过程中进行了一些假设和简化。其中之一是假设所有滑移面上的材料同时达到极限平衡状态，而实际上材料的极限平衡往往是逐步实现的。极限平衡法的另一个假设与滑动面有关。边坡的滑动面在发生破坏前通常是未知的，而在计算边坡的稳定性时，需要预先假设边坡的形状和位置，找到最小安全系数来确定一个潜在的滑移面。
随着计算机技术的发展，许多学者采用数值分析方法来研究碎石土边坡的稳定性。有限元法（finite element method，FEM）可以模拟计算处边坡的滑移面和安全系数，被广泛应用于边坡稳定性分析[10]。Napoli等[11]分别有限元法和极限平衡法对不同含石量的边坡进行了稳定性分析。庄锦亮等[12]基于FLAC3D和Janbu法计算不同内摩擦角和黏聚力边坡的安全系数，结果表明内摩擦角对边坡稳定性的影响更明显。然而，有限元法在建模时把所有介质视为连续体，当边坡由岩土或砂土组成时这一假设是合理的。然而碎石土由碎石和细粒土组成，其同时表现出连续介质和离散介质的特征，造成有限元法的这一假设变得不再合适。因此，一些研究者采用离散元法（discrete element method，DEM）来研究碎石土边坡的稳定性。离散元法假设材料是由大量的单独粒子组成的，它们可以相互独立地运动，只在接触点相互作用。李存柱等[13]基于离散单元法发现碎石的形状会影响材料宏观力学性能，并且建立了碎石形状与其宏观力学性能之间的关系。陆烨等[14]用离散单元法对碎石土边坡的稳定性进行了分析，发现碎石的含量、形状和大小会影响边坡的安全系数。但是由于需要考虑所有颗粒的相互作用，离散元法的计算效率较低。
目前关于碎石土边坡模型试验的研究较少，多数研究集中于碎石土的单元体试验。彭东黎等[15]基于大型的室内直剪试验，对含石量及含水量与碎石土黏聚力和内摩擦角的关系进行了深入研究。Wang[16]采用高能X射线计算机断层成像（CT）方法研究了三轴试验中碎石含量对碎石土细观结构变化和相关应变局部化行为的影响。王腾等人[17]用铝棒模拟砾石，对碎石土进行了平面应变试验，发现碎石主要通过转动阻力影响剪切带的发展。但是单元体试验无法重现碎石土边坡复杂的地质情况，不能准确地描述其破坏过程。
碎石土具有天然的多尺度结构，其变形和强度特性很大程度受其细观结构的影响。但目前相关研究很少从宏细观尺度深入地分析碎石土边坡的失效机制。本文基于数字图像技术，对不同含石量的碎石土边坡进行模型试验，从宏细观尺度研究碎石土边坡的失稳机制。试验结果表明，含石量对碎石土边坡的承载力和位移具有显著的控制效果，并且碎石会影响剪切带的发展。
1. 试验概况
1.1 试验装置
试验所用模型箱尺寸为600 mm×290 mm×350 mm（长×宽×高），四个面均为透明面，便于使用数码相机记录试验过程中砂土边坡侧面土体连续变形过程。加载装置为万能材料试验机，通过对边坡坡顶尺寸为100 mm×290 mm×50 mm的加载板施加荷载，如图1所示。
1.2 试样制备
本试验中试样是粒径2～10 mm的砾石与d50为0.29 mm的福建标准砂混合配制而成的碎石土，各试样的级配曲线如图2所示。为保证局部场拍摄效果，对局部的碎石土进行染色处理。
制备试样时，首先将所需碎石砂土烘干。然后按3%的含水率加水搅拌直至均匀，为保证密度控制在1.74 g/cm3，每次称量后分层填筑进模型箱填筑，完成的模型如图3所示，坡高250 mm，坡角为50°。
1.3 图像采集
使用4240万有效像素的数码相机在试验期间连续拍摄，捕捉全场土体位移的图像，同时使用微距摄像头拍摄局部场土体变形。为了减少自然光对图像质量的影响，在试验过程中使用两个摄影灯提供照明。试验结束后，将视频中的图像提取并导入自行编制的图像处理程序进行计算。
2. 试验结果及分析
2.1 坡顶荷载-沉降曲线
为了减少壁面摩擦对边坡承载力的影响，在模型箱的壁面涂抹凡士林作为润滑剂。图4为边坡的荷载与位移关系曲线和极限承载力。
![]()
图 4 不同含石量边坡的P-s曲线和极限承载力Figure 4. P-s curves and ultimate bearing capacity curves of the slopes with different stone contents从图4（a）可以看出，边坡的P-s曲线受碎石含量的影响。P-s曲线变化大致可以分为三个阶段。第一阶段，随着荷载的增加，坡顶沉降接近线性增大，坡顶砂土处于整体压密阶段。随含石量增加，曲线的斜率增加。第二阶段，随着荷载逐渐接近峰值，荷载的增长率逐渐降低。荷载达到峰值后为第三阶段，在此阶段，不同含石量的P-s曲线呈现不同的形式。当含石量小于70%时，边坡的承载力有明显的软化阶段。而含石量大于70%时，承载力在第三阶段没有明显的软化现象。并且，含石量越大，边坡达到承载力峰值的位移越大。边坡的极限承载力也就是试验中的峰值承载力，本文中T为加载时刻至边坡的极限承载力总时间。表1列出不同含石量的碎石土边坡所需的总时间T，从中可以看出随含石量增加，荷载达到极限承载力所需的时间逐渐增加，但是在低含石量和高含石量时，增加幅度较小。
表 1 不同含石量碎石土边坡总时间（T）Table 1. Time of gravel soil slope with different stone contents含石量/% T/s 含石量/% T/s 0 150 50 535 10 189 60 624 20 224 70 700 30 295 80 715 40 426 图4（b）比较了不同含石量边坡的极限承载力。从图中可以看出，边坡的极限承载力受碎石含量的影响。当含石量低于20%时，边坡受含石量的影响较小，这是由于此时碎石土的力学性质主要依赖于砂土，碎石悬浮在砂土之中，对边坡的极限承载力贡献较小。而当含石量高于20%且小于70%时，边坡的极限承载力随含石量增大而急剧增加，此时边坡内的碎石形成骨架结构，承载力受碎石的影响突显，承载力由碎石和砂土共同承担。而当含石量达到70%时，边坡内的碎石形成了架空结构，边坡中的砂土悬浮在碎石间，碎石土的力学性质更接近于岩体；在此基础上含石量增加，极限承载力基本没有改变。因此含石量对边坡承载力的影响存在两个阈值，下阈值为20%，上阈值为70%。
2.2 不同含石量位移云图分析
根据含石量对边坡极限承载力影响的上、下阈值，本文选取了三个区间中各一含石量的碎石土边坡进行研究，即含石量为10%、50%和80%。将试验过程中拍摄的视频每5 s截取一张图像用于DIC的相关计算，得到边坡的位移增量。图5为不同含石量边坡达到极限承载力时的位移矢量增量，图中箭头方向为土体发生位移的方向，箭头的长度代表土体位移的大小。
![]()
图 5 不同含石量边坡位移矢量增量Figure 5. Displacement vector increment of slope with different stone content从图5可知，在边坡达到极限承载力时，不同含石量碎石土边坡的土体位移趋势是一样的。在加载板下方，位移矢量的方向靠近垂直方向，该区域的土体主要发生竖直位移。越靠近临坡面，位移矢量接近水平，土体位移以水平方向为主。根据土体的变形情况可以分为三个区域：稳定区、剪切区和滑移区。在稳定区，土体几乎没有发生位移，位移矢量呈现点状；在滑移区，土体发生较大的位移，并且以水平位移为主；剪切区介于稳定区和滑移区之间，剪切区的范围很窄，但位移梯度变化很大。比较不同含石量边坡的位移矢量长度可以发现，边坡的位移增量随着含石量的增加而减小，这是因为含石量增加，碎石之间的接触逐渐增加并形成碎石骨架，碎石土的内摩擦角增大，边坡抵抗变形的能力增强，因此其位移增量减小。
以位移增量0.02 mm作为土体发生变形的范围，画出位移包络线，如图6所示。从图中可以看出含石量增加，土体发生变形的范围越大。这是由于碎石之间互相嵌固，机械咬合力增大，边坡碎石发生位移和旋转时会带动更大范围内碎石土受力变形，因此随着含石量的增加，土体发生位移的范围也更大。对比不同含石量的边坡位移包络线形状可以发现含石量增大，包络线形状变得不规则且曲折。主要原因是碎石的强度和刚度都较大，土体变形的滑移面往往会沿着强度和刚度相对更低的碎石与碎石、碎石与砂土的接触面发展，从而导致其位移包络线变得曲折。
![]()
图 6 不同含石量边坡土体包络线Figure 6. Displacement envelope of slope with different stone content2.3 剪应变云图分析
当荷载达到峰值后边坡发生失稳破坏，部分土体会沿着某一滑动面突然出现明显的运动，这个滑动面称之为剪切带，而这个滑移面的附近发生显著的应变局部化现象。图7为不同含石量碎石土边坡达到极限承载力时剪应变增量云图，以逆时针为正。
![]()
图 7 不同含石量边坡剪应变增量云图Figure 7. Cloud diagram of shear strain increment of slope with different stone content由图7可以看出，碎石会影响边坡中剪切带的发展。当含石量为10%时，边坡内只有一条主剪切带，在滑移体内只有少量的剪应变较大的部位，剪切带也较为平顺光滑。而当含石量较高时，滑移体内的次剪切带随着含石量的增加而逐渐增多，并且剪切带形状变得曲折不规则。这是由于碎石的本身的强度和刚度较高，导致剪切带在发展路径经过碎石骨架时，会沿着碎石与碎石、碎石与砂土的接触面发展，因此剪切带可能发生绕石或分叉，从而在滑移体内产生多条次剪切带。
3. 局部场结果及分析
3.1 局部场剪应变云图分析
当含石量较低时，碎石悬浮在砂土之中，而含石量较高时碎石形成了架空结构，边坡中的砂土悬浮在碎石间。因此本节选择了含石量50%碎石土边坡的局部场作为研究对象，在该含石量时碎石与砂土共同承担上部荷载，两种材料间的相互作用更加复杂，更能揭示碎石和周围砂颗粒的细观行为对剪切带发展的影响。图8分别拍摄了含石量50%碎石土边坡的上部和下部局部场图像，上部局部场在后文中称为局部场一，其计算区域尺寸为84 mm×48 mm；下部局部场为局部场二，其计算区域尺寸为44 mm×28 mm。
![]()
图 8 局部场一和局部场二位置示意图（单位：mm）Figure 8. Location map of the local field I and local field II (unit: mm)局部场土体发生剪切破坏时，会出现明显的应变局部化。图9为不同时刻局部场剪应变增量云图。由图9可以发现，在1/4T时刻，局部场一土体没有变形，此处剪切应变增量值几乎为零。而加载到1/2T时，在滑移面出现了应变局部化现象，并且剪应变连接并贯通局部场一，说明此时局部场一已经发生了剪切破坏。在剪切带外的滑移区内，分布着剪应变较大的单元。随着荷载变大，滑移区内剪应变较大的单元变多，部分形成次剪切带。这是由于碎石影响了剪切带的发展路。与局部场一相比，局部场二的剪切带形成时间更晚，在3/4T时刻时，才能看到明显的应变局部化现象。
对比全场的剪应变增量云图，可以发现在高含石量的边坡内，剪切带往往从开始的只有一条或两条主剪切带逐渐发展成“一主多次”的剪切带形式。这说明碎石对剪切带的发展有明显的影响作用。
3.2 碎石对剪切带发展的影响
为了明确碎石对剪切带的影响，选取了局部场一中有代表性的区域进行放大，如图10所示。图中虚线红框中为选定区域，并进行编号S1～S6。
在放大的区域，用黑色虚线描出碎石边界，用红色虚线会出剪切带位置，如图11所示。从图中可以看出，当剪切带经过碎石时，剪切带会出现几种不同的绕石模式。S2和S3处图中可以看到当剪切带经过碎石时，发生了单边绕石，碎石左右两侧都可能是剪切带的绕石方向。S1、S5和S6中剪切带的绕石方式是分叉，由一条剪切带分叉成两条甚至多条剪切带。对比这两种模式可以发现，当剪切带发展的方向与碎石的长轴方向成锐角时，剪切带大概率会以分叉的模式继续发展，当剪切带发展的方向与碎石的长轴方向成钝角时，剪切带会以单边绕石的模式继续发展，发展方向取决于碎石和剪切带之间的位置关系。S1、S3、S4和S6可以看到当发生这两种绕石模式时，剪切带会穿越碎石与碎石接触面。
选取S6区域中2个碎石和其周边20个砂土颗粒描绘出其在不同时刻的质心坐标和长轴角度，进一步验证碎石对剪切带的影响，如图12所示。X和Y轴均为图像的像素坐标，颗粒边上数字为编号，碎石1～2，砂颗粒1～20。两个碎石在1/4T时相互接触形成骨架，砂颗粒1～17分布在碎石骨架外，砂颗粒18～20位于碎石骨架内。当加载到1/2T时刻时，碎石和砂颗粒发生的位移和旋转角度都较小，两个碎石逐渐分开，砂颗粒与碎石的相对位置没有明显改变。继续加载，位于上方的碎石和砂颗粒出现了比较明显的位移和旋转角度，而下方的碎石基本没有运动。此时砂颗粒和碎石之间的相对位置发生改变，有部分砂颗粒沿着碎石左侧运动，在碎石之间有砂颗粒挤入碎石骨架，剩余的砂颗粒沿着下方碎石的右侧运动。碎石影响了土体变形，滑移面由一个分叉成多个滑移面。
![]()
图 12 不同时刻颗粒的位移和旋转Figure 12. Displacement and rotation of particles at different moments通过对像素标定，即一个像素值等于0.05 mm，计算得到各颗粒实际位移值，位移以向下为正和向右为正，旋转角度以逆时针为正，如表2所示。从表中可以看出，砂颗粒的位移和旋转角度大于碎石。碎石和周边的砂颗粒的运动行为存在差异，主要原因是一方面是当含石量为50%时，尽管碎石形成骨架结构与砂颗粒一起承受荷载，但是砂颗粒仍是主要的承力介质，导致砂颗粒发生更剧烈的运动，另一方面是碎石的内摩擦角比砂颗粒更大，碎石的运动明显弱于砂颗粒。碎石与周边砂土运动行为不协调，使得砂颗粒会沿着碎石边缘或者碎石之间的接触面运动。这也是碎石影响剪切带发展的原因之一。
表 2 颗粒位移和旋转角度Table 2. Summary table of the particle displacement and rotation angle颗粒 水平位移/mm 竖直位移/mm 旋转角度/（°） 颗粒 水平位移/mm 竖直位移/mm 旋转角度/（°） 碎石1 3.87 5.17 16 砂颗粒10 2.75 8.25 −36 碎石2 1.75 3.01 1 砂颗粒11 1.78 5.93 −20 砂颗粒1 7.88 8.54 122 砂颗粒12 2.84 7.40 −25 砂颗粒2 8.90 7.30 110 砂颗粒13 2.04 7.20 −94 砂颗粒3 10.19 5.68 90 砂颗粒14 5.55 4.69 −80 砂颗粒4 9.41 6.94 114 砂颗粒15 4.69 4.28 117 砂颗粒5 9.25 5.98 50 砂颗粒16 5.41 4.62 56 砂颗粒6 8.39 4.31 52 砂颗粒17 2.41 3.91 77 砂颗粒7 5.74 7.67 22 砂颗粒18 2.14 6.35 −22 砂颗粒8 4.26 4.5 160 砂颗粒19 3.31 4.24 30 砂颗粒9 7.23 1.71 10 砂颗粒20 2.70 3.92 −45 对各个区域颗粒的运动分析，总结出碎石对剪切带发展路径影响的五种绕石模式，如图13所示，箭头为剪切带的发展方向。对比这五种剪切带的绕石模式，可以发现碎石会导致剪切带影响的范围变广，长度变长，从而提高了边坡的抗滑能力，提高了边坡的稳定性，增加了边坡的极限承载力。
![]()
图 13 局部位置剪切带绕石示意图Figure 13. Schematic diagram of shear zone around stone in local field position3.3 局部场孔隙率分析
当碎石土发生剪切破坏时，碎石骨架发生破坏和重构导致孔隙率改变。研究土体破坏过程中孔隙率的变化，有利于了解碎石土的破坏机制。
图14给出了局部场一和局部场二不同区域孔隙率的时程曲线。从图14（a）可以发现，局部场一的碎石土在未加载时，孔隙率为0.31左右。随着荷载增加，局部场一整体的孔隙率开始缓慢减小。这是因为一开始边坡处于整体压密的阶段，使得孔隙率降低。当加载到0.46T左右时，此时孔隙率最小，为0.28左右。稳定区的孔隙率在此之后开始保持稳定，说明局部场一已经完成压密。而剪切带的孔隙率开始突然增加，增长趋势维持0.18T左右，在图中用虚线标出，此时孔隙率达到0.35左右，然后在这一值上下波动。剪切带的形成过程中，碎石颗粒会发生位移、旋转等运动导致土体的孔隙率产生变化，因此剪切内孔隙率时程曲线的拐点可以认定为剪切带的初始化时间，孔隙率变化的这段时间可以看作剪切带的形成过程。滑移区的孔隙率在0.46T后和剪切带一样，开始突然增加，不过达到稳定时的值小于剪切带，为0.32左右。这是因为滑移区内也出现次剪切带，从而导致了孔隙率上升。局部场二的孔隙率的变化趋势与局部场一相似，不过局部场二剪切带的孔隙率在大约0.65T时才突然增大，并且剪切带发展的时间为0.11T比局部场一更短。这说明边坡剪切带发展是一个逐渐加速过程。
![]()
图 14 局部场不同区域孔隙率时程曲线Figure 14. Time history curves of porosity in different regions of the local field4. 结论
本文基于数字图像技术，通过静力超载法对碎石土边坡进行模型试验，从宏细观角度研究了碎石土边坡的失稳机制，得到以下几点结论：
（1）含石量会影响碎石土边坡的承载力和变形特性且存在两个阈值，下阈值为20%，上阈值为70%。当含石量小于20%时，极限承载力随着含石量增大而缓慢提高，边坡受含石量的影响较小；当含石量高于20%且小于70%时，边坡的极限承载力随含石量增大而急剧增加；当含石量大于70%时，含石量增加，极限承载力增加较小。
（2）碎石会影响边坡的土体变形和剪切带的发展。碎石与周边砂颗粒的运动行为存在差异，使得剪切带在经过碎石骨架时，其发展路径存在五种不同的绕石模式。
（3）在剪切前，碎石土的孔隙率会因为边坡被压密而逐渐减小。在剪切后，由于强烈的剪切应变和碎石土骨架的破坏重构，剪切带内的孔隙率在剪切过程中突然增大，并在剪切带形成后稳定。可以通过孔隙率的变化研究剪切带的初始化和发展。
-
![]()
图 3 不同形状试块Rn值与正转转速的关系
Figure 3. Relationship between forward rotation speeds and Rn values of blocks with different shapes
![]()
图 4 不同形状试块Rn值与反转转速的关系
Figure 4. Relationship between reverse rotation speeds
and Rn values of blocks with different shapes ![]()
图 5 试块冲击回弹特征分类示意图
Figure 5. The classification diagram of the impact-rebound characteristics of the blocks
![]()
图 7 正转试验中I-1类型试块IPC与Rn的关系
Figure 7. The relationship between IPC and Rn of I-1 type blocks in forward rotation test
![]()
图 9 正转试验中I-2类型试块IPC与Rn的关系
Figure 9. The relationship between IPC and Rn of I-2 type blocks in forward rotation test
![]()
图 8 反转试验中I-1类型试块IPC与Rn的关系
Figure 8. The relationship between IPC and Rn
of I-1 type blocks in reverse rotation test ![]()
图 10 正转试验I-2类型试块IPC对Rn的影响示意图
Figure 10. Schematic diagram of the impact of IPC on Rn in forward transfer test I-2 type test block
![]()
图 11 正转试验F-2条件下试块对坡面第一次冲击与第二次冲击剧烈程度及接触角（θ，θ1）对比
Figure 11. Comparison of the intensity and contact angles (θ, θ1) of the first impact and the second impact between the blocks and the slope under F-2 condition in forward rotation test
![]()
图 12 正转试验B-2条件下接触角（θ，θ1）对比
Figure 12. Comparison of contact angles (θ, θ1 ) under B-2 condition in forward rotation test
![]()
图 13 反转试验中I-2类型试块IPC与Rn的关系
Figure 13. The relationship between IPC and Rn of I-2 type test block in reverse test
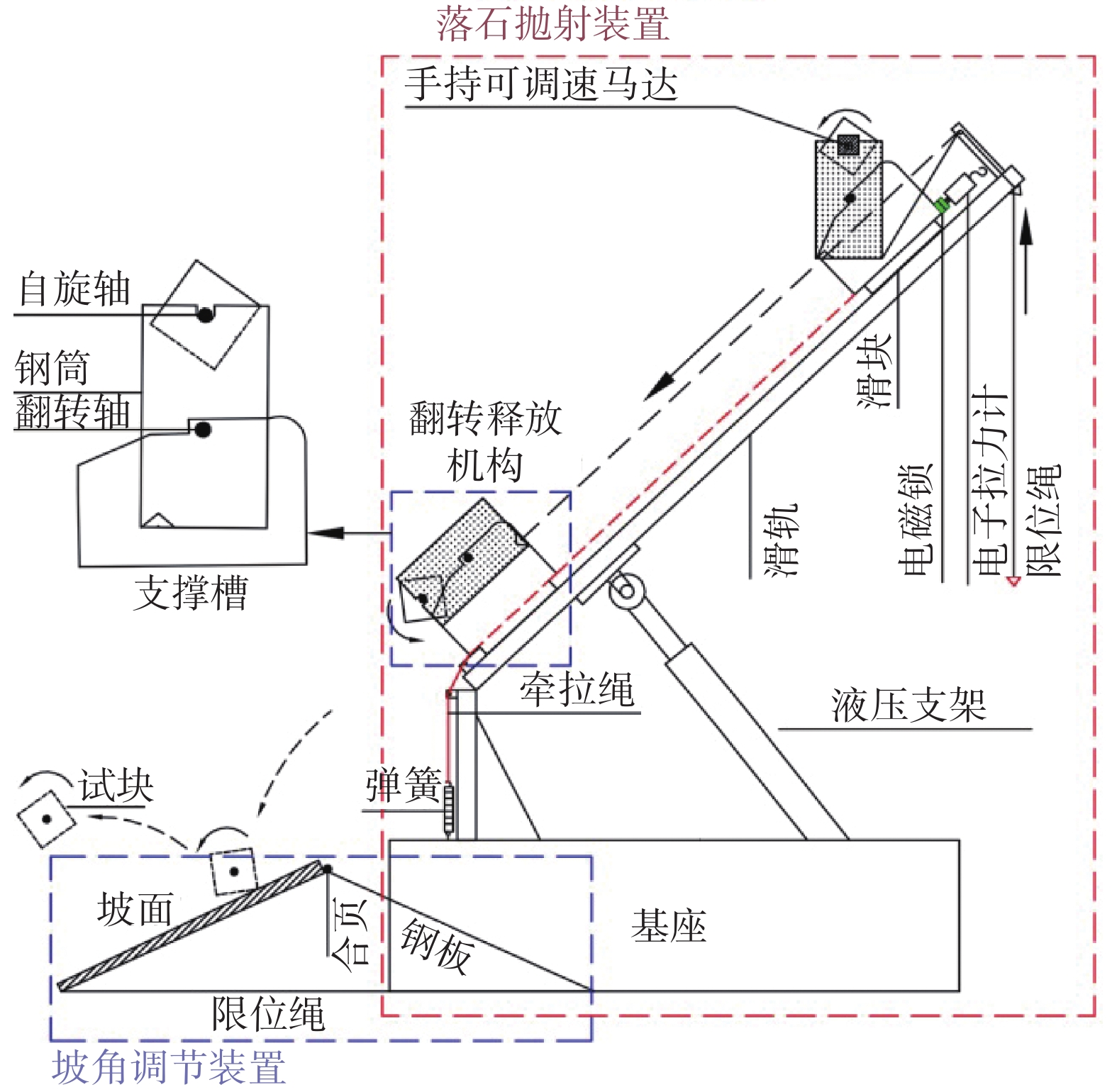
表 1 试块与坡面特征参数及试验初始条件
Table 1 The characteristic parameters of the block and slope and the initial conditions of the test
试块特征 岩石类型 形状 尺寸 V/（m∙s−1) α/(°) 初始转速/
(r∙min−1)特征长度 值/mm 灰岩 正方体 边长 40.3 3.5 40 100~500
（正/反转）圆盘 直径/厚度 58.6/24.3 圆柱 直径/高 33.78/73 坡面特征 岩石类型 形状 尺寸 特征长度 值/mm 灰岩 长方体 长/宽/高 700/500/150 
下载: 导出CSV
-
[1] 俸锦福, 张俊红, 朱彬, 等. 边坡滚石运动轨迹分段循环算法[J]. 中国地质灾害与防治学报,2011,22(4):96 − 101. [FENG Jinfu, ZHANG Junhong, ZHU Bin, et al. Segmented loop algorithm of theoretical calculation of trajectory of rockfall[J]. The Chinese Journal of Geological Hazard and Control,2011,22(4):96 − 101. (in Chinese with English abstract) DOI: 10.3969/j.issn.1003-8035.2011.04.021 [2] ASTERIOU P, SAROGLOU H, TSIAMBAOS G. Geotechnical and kinematic parameters affecting the coefficients of restitution for rock fall analysis[J]. International Journal of Rock Mechanics and Mining Sciences,2012,54:103 − 113. DOI: 10.1016/j.ijrmms.2012.05.029
[3] 贺凯, 高杨, 殷跃平, 等. 基于岩体损伤的大型高陡危岩稳定性评价方法[J]. 水文地质工程地质,2020,47(4):82 − 89. [HE Kai, GAO Yang, YIN Yueping, et al. Stability assessment methods for huge high-steep unstable rock mass based on damage theory[J]. Hydrogeology & Engineering Geology,2020,47(4):82 − 89. (in Chinese with English abstract) [4] 章广成, 向欣, 唐辉明. 落石碰撞恢复系数的现场试验与数值计算[J]. 岩石力学与工程学报,2011,30(6):1266 − 1273. [ZHANG Guangcheng, XIANG Xin, TANG Huiming. Field test and numerical calculation of restitution coefficient of rockfall collision[J]. Chinese Journal of Rock Mechanics and Engineering,2011,30(6):1266 − 1273. (in Chinese with English abstract) [5] 李娟, 何亮, 荀晓慧. 强震作用下崩塌滚石冲击耗能损伤演化分析[J]. 水文地质工程地质,2022,49(2):157 − 163. [LI Juan, HE Liang, XUN Xiaohui. An evolution analysis of the impact energy damage of collapsed rolling stones under strong earthquakes[J]. Hydrogeology & Engineering Geology,2022,49(2):157 − 163. (in Chinese with English abstract) [6] 孙敬辉, 石豫川. 重庆甑子岩崩塌落石动力学特征及危险性分区[J]. 中国地质灾害与防治学报,2019,30(3):6 − 11. [SUN Jinghui, SHI Yuchuan. Dynamics and hazard zoning of collapse and rockfall in Zengziyan, Chongqing[J]. The Chinese Journal of Geological Hazard and Control,2019,30(3):6 − 11. (in Chinese with English abstract) [7] 何思明, 吴永, 李新坡. 滚石冲击碰撞恢复系数研究[J]. 岩土力学,2009,30(3):623 − 627. [HE Siming, WU Yong, LI Xinpo. Research on restitution coefficient of rock fall[J]. Rock and Soil Mechanics,2009,30(3):623 − 627. (in Chinese with English abstract) DOI: 10.3969/j.issn.1000-7598.2009.03.008 [8] 何宇航, 裴向军, 梁靖, 等. 基于Rockfall的危岩体危险范围预测及风险评价—以九寨沟景区悬沟危岩体为例[J]. 中国地质灾害与防治学报,2020,31(4):24 − 33. [HE Yuhang, PEI Xiangjun, LIANG Jing, et al. Risk assessment and range prediction of dangerous rockmass based on rockfall: A case study of the Xuangou Collapse[J]. The Chinese Journal of Geological Hazard and Control,2020,31(4):24 − 33. (in Chinese with English abstract) [9] BOURRIER F, BERGER F, TARDIF P, et al. Rockfall rebound: comparison of detailed field experiments and alternative modelling approaches[J]. Earth Surface Processes and Landforms,2012,37(6):656 − 665. DOI: 10.1002/esp.3202
[10] FERRARI F, GIANI G, APUANI T. Why can rockfall normal restitution coefficient be higher than one[J]. Rend Online Soc Geol It,2013,24:122 − 124.
[11] SPADARI M, GIACOMINI A, BUZZI O, et al. In situ rockfall testing in new south Wales, Australia[J]. International Journal of Rock Mechanics and Mining Sciences,2012,49:84 − 93. DOI: 10.1016/j.ijrmms.2011.11.013
[12] JI Z M, CHEN Z J, NIU Q H, et al. Laboratory study on the influencing factors and their control for the coefficient of restitution during rockfall impacts[J]. Landslides,2019,16(10):1939 − 1963. DOI: 10.1007/s10346-019-01183-x
[13] JI Z M, CHEN Z J, NIU Q H, et al. A calculation model of the normal coefficient of restitution based on multi-factor interaction experiments[J]. Landslides,2021,18(4):1531 − 1553. DOI: 10.1007/s10346-020-01556-7
[14] 姬中民, 唐一举, 伍法权, 等. 落石形状和尺寸对恢复系数影响的室内试验研究[J]. 岩土力学,2021,42(3):665 − 672. [JI Zhongmin, TANG Yiju, WU Faquan, et al. Laboratory investigation of the effect of rockfall shape and size on coefficient of restitution[J]. Rock and Soil Mechanics,2021,42(3):665 − 672. (in Chinese with English abstract) [15] GIANI G P, GIACOMINI A, MIGLIAZZA M, et al. Experimental and theoretical studies to improve rock fall analysis and protection work design[J]. Rock Mechanics and Rock Engineering,2004,37(5):369 − 389. DOI: 10.1007/s00603-004-0027-2
[16] ASTERIOU P, TSIAMBAOS G. Empirical model for predicting rockfall trajectory direction[J]. Rock Mechanics and Rock Engineering,2016,49(3):927 − 941. DOI: 10.1007/s00603-015-0798-7
[17] BUZZI O, GIACOMINI A, SPADARI M. Laboratory investigation on high values of restitution coefficients[J]. Rock Mechanics and Rock Engineering,2012,45(1):35 − 43. DOI: 10.1007/s00603-011-0183-0
[18] GIACOMINI A, THOENI K, LAMBERT C, et al. Experimental study on rockfall drapery systems for open pit highwalls[J]. International Journal of Rock Mechanics and Mining Sciences,2012,56:171 − 181. DOI: 10.1016/j.ijrmms.2012.07.030
[19] HEIDENREICH B. Small- and half scale experimental studies of rockfall impacts on sandy slopes [D]. Lausanne: Swiss Federal Institute of Technology Lausanne, 2004.
[20] WYLLIE D C. Calibration of rock fall modeling parameters[J]. International Journal of Rock Mechanics and Mining Sciences,2014,67:170 − 180. DOI: 10.1016/j.ijrmms.2013.10.002
[21] ASTERIOU P, SAROGLOU H, TSIAMBAOS G. Rockfalls: influence of rock hardness on the trajectory of falling rock blocks[J]. Bulletin of the Geological Society of Greece,2013,47(4):1684 − 1693. DOI: 10.12681/bgsg.11033
[22] 陈涛, 陈志坚, 孟子耀. 基于Trajec 3D的硬岩人工路堑边坡滚石运动范围预测[J]. 中国地质灾害与防治学报,2019,30(5):37 − 41. [CHEN Tao, CHEN Zhijian, MENG Ziyao. Movement prediction of falling boulders in artificial cutting slope of hard rock based on Trajec 3D[J]. The Chinese Journal of Geological Hazard and Control,2019,30(5):37 − 41. (in Chinese with English abstract) [23] ASTERIOU P, TSIAMBAOS G. Effect of impact velocity, block mass and hardness on the coefficients of restitution for rockfall analysis[J]. International Journal of Rock Mechanics and Mining Sciences,2018,106:41 − 50. DOI: 10.1016/j.ijrmms.2018.04.001
[24] ANSARI M K, AHMAD M, SINGH R, et al. Correlation between Schmidt hardness and coefficient of restitution of rocks[J]. Journal of African Earth Sciences,2015,104:1 − 5. DOI: 10.1016/j.jafrearsci.2015.01.005
[25] FITYUS S G, GIACOMINI A, BUZZI O. The significance of geology for the morphology of potentially unstable rocks[J]. Engineering Geology,2013,162:43 − 52. DOI: 10.1016/j.enggeo.2013.05.007
[26] MEYERS M A. Dynamic behavior of materials[M]. New York: John Wiley & Sons Inc, 1994.
-
期刊类型引用(2)
1. 李睿，周洪福，李树武，巨广宏，刘万林，唐文清. 大跨度高埋深地下洞室群开挖后涌水量预测. 水文地质工程地质. 2025(01): 179-189 . 
百度学术
2. 蔡光辉. 库水升降对猫溪沟水库右岸坡涉水堆渣体稳定性分析研究. 建筑技术开发. 2024(09): 155-158 . 百度学术
其他类型引用(0)
计量
- 文章访问数: 287
- HTML全文浏览量: 135
- PDF下载量: 188
- 被引次数: 2
邮件订阅
RSS